Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:

Câu hỏi:

Cho đường tròn (C): x² + y² – 2x – 4y + 1 = 0. Gọi d₁, d₂ lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d₁ và d₂ là:

A. (3; 0);               

Đáp án chính xác

B. (–3; 0);             

C. (0; 3);               

D. (0; –3).

Trả lời:

Ta viết phương trình d₁:
Ta có 3² + 2² – 2.3 – 4.2 + 1 = 0 (đúng).
Do đó điểm M ∈ (C).
Phương trình đường tròn (C) có dạng: x² + y² – 2ax – 2by + c = 0, với a = 1, b = 2, c = 1.
Suy ra tâm I(1; 2), bán kính R = $\sqrt{a^2+b^2-c}=\sqrt{1+4-1}=2$ .
Phương trình d₁ là: (1 – 3)(x – 3) + (2 – 2)(y – 2) = 0
⇔ –2(x – 3) = 0 ⇔ x – 3 = 0.
Tương tự, ta viết phương trình d₂:
Ta có 1² + 0² – 2.1 – 4.0 + 1 = 0 (đúng).
Do đó N ∈ (C).
Phương trình d₂ là: (1 – 1)(x – 1) + (2 – 0)(y – 0) = 0
⇔ y = 0.
Gọi A là giao điểm của d₁ và d₂.
Suy ra tọa độ A là nghiệm của hệ phương trình: 
$\{\begin{array}{l}x-3=0\\ y=0\end{array}\iff \{\begin{array}{l}x=3\\ y=0\end{array}$

Khi đó ta có tọa độ A(3; 0).
Vậy ta chọn phương án A.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:
   
   

   Câu hỏi:
   

   Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:

   A. I(1; 0);              

   B. I(0; 1);              

   Đáp án chính xác

   C. I(–1; 0);            

   D. I(0; –1).

   Trả lời:

   Đáp án đúng là: B
   Ta có I là trọng tâm của ∆ABC.
   Do đó $\{\begin{array}{l}{x}_I=\frac{x_A+x_B+x_C}{3}=\frac{-4+2+2}{3}=0\\ y_I=\frac{y_A+y_B+y_C}{3}=\frac{1+4-2}{3}=1\end{array}$
   Suy ra I(0; 1).
   Vậy ta chọn phương án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho u→=(4;5)  và v→=(3;a)  . Tìm a để u→⊥v→
   
   

   Câu hỏi:
   

   Cho $\overrightarrow{u}=(4;5)$  và $\overrightarrow{v}=(3;a)$  . Tìm a để $\overrightarrow{u}\perp \overrightarrow{v}$

   A. $a=\frac{12}{5}$

   B. $a=-\frac{12}{5}$

   Đáp án chính xác

   C. $a=\frac{5}{12}$

   D. $a=-\frac{5}{12}$

   Trả lời:

   Đáp án đúng là: B
   Ta có $\overrightarrow{u}\perp \overrightarrow{v}\iff \overrightarrow{u}.\overrightarrow{v}=0$

   ⇔ 4.3 + 5.a = 0    
   ⇔ 12 + 5a = 0
   ⇔ 5a = –12

   Vậy ta chọn phương án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
   
   

   Câu hỏi:
   

   Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:

   A. (3; –2);             

   B. (5; 0);               

   C. (3; 0);               

   Đáp án chính xác

   D. (5; –2).

   Trả lời:

   Đáp án đúng là: C
   

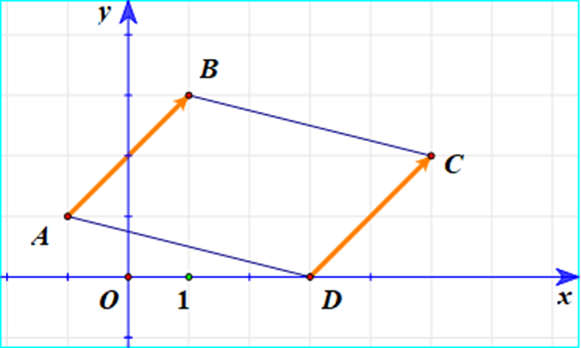
   Với A(–1; 1), B(1; 3), C(5; 2) và D(x_D; y_D) ta có:
   $\overrightarrow{AB}=(x_B-x_A;y_B-y_A)=(1-(-1);3-1)=(2;2)\overrightarrow{DC}=(x_C-x_D;y_C-y_D)=(5-x_D;2-y_D)$
   Tứ giác ABCD là hình bình hành ⇔ $\overrightarrow{AB}=\overrightarrow{DC}$
   $\iff \{\begin{array}{l}2=5-x_D\\ 2=2-y_D\end{array}\iff \{\begin{array}{l}{x}_D=3\\ y_D=0\end{array}$
   Ta suy ra tọa độ D(3; 0).
   Vậy ta chọn phương án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng  là:
   
   

   Câu hỏi:
   

   Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng  là:

   A. x ∈ ∅;               

   B. x = 1;                

   C. x = 11;              

   D. x = 11 hoặc x = 1.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Ta có $AB=\sqrt{{(x_B-x_A)}^2+{(y_B-y_A)}^2}Suy ra AB=\sqrt{{(x-6)}^2+{(9+1)}^2}=\sqrt{{(x-6)}^2+{10}^2}$
   Theo đề, ta có AB = $5\sqrt{5}$
   $\iff \sqrt{{(x-6)}^2+{10}^2}=5\sqrt{5}$

   ⇔ x² – 12x + 36 + 100 = 125
   ⇔ x² – 12x + 11 = 0
   ⇔ x = 11 hoặc x = 1.
   Vậy ta chọn phương án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho a→=(1;2), b→=(−2;3). Góc giữa hai vectơ u→=3a→+2b→và v→=a→−5b→   bằng
   
   

   Câu hỏi:
   

   Cho $\overrightarrow{a}=(1;2), \overrightarrow{b}=(-2;3)$. Góc giữa hai vectơ $\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}$và $\overrightarrow{v}=\overrightarrow{a}-5\overrightarrow{b}$   bằng

   A. 45°;        

   B. 60°;                  

   C. 90°;                  

   D. 135°.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Với $\overrightarrow{a}=(1;2), \overrightarrow{b}=(-2;3)$ ta có:
   +) $3\overrightarrow{a}=(3.1;3.2)=(3;6), 2\overrightarrow{b}=(2.(-2);2.3)=(-4;6)$
   Suy ra $\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}=(3-4;6+6)=(-1;12)$
   $\overrightarrow{a}=(3;4), 5\overrightarrow{b}=(5.(-2);5.3)=(-10;15)Suy ra \overrightarrow{v}=\overrightarrow{a}-5\overrightarrow{b}=(3-(-10);4-15)=(13;-11)$
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====