Câu hỏi:
Cho điểm M(x; y) nằm trên hypebol .
a) Chứng minh rằng F1M2 – F2M2 = 4cx.
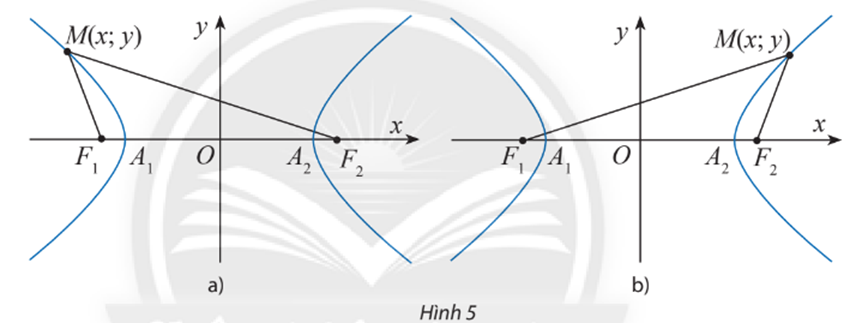
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A1(–a; 0) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF2 – MF1 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A2(a; 0) (Hình 5 b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF1 – MF2 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
Trả lời:
Hướng dẫn giải
a) F1M2 = + = + = ;
F2M2 = +=
F1M2 – F2M2 = () – () = 4cx.
b) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)(–2a) = 4cx
=> MF1 + MF2 = = –x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = – + (–2a) => 2MF1 = –
– 2a
=> MF1 =
(MF1 + MF2) – (MF1 – MF2) = – – (–2a) => 2MF2 = – + 2a
=> MF2 = a –c/a x.
c) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)2a = 4cx
=> MF1 + MF2 = = x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = + 2a => 2MF1 = + 2a
=> MF1 = a + x.
(MF1 + MF2) – (MF1 – MF2) = – 2a => 2MF2 = – 2a
=> MF2 = – a +x.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc x2a2−y2b2=1.
a) Hãy giải thích vì sao nếu điểm M(x0; y0) thuộc hypebol thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc hypebol (H.3.12).
b) Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm M(x0; y0) thuộc hypebol, hãy so sánh |x0| với a.
Câu hỏi:
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc .
a) Hãy giải thích vì sao nếu điểm M(x0; y0) thuộc hypebol thì các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc hypebol (H.3.12).
b) Tìm toạ độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm M(x0; y0) thuộc hypebol, hãy so sánh |x0| với a.Trả lời:
a) Nếu điểm M(x0; y0) thuộc hypebol thì ta có:
Ta có: nên các điểm có toạ độ (x0; –y0), (–x0; y0), (–x0; –y0) cũng thuộc elip.
b)
+) Gọi A là giao điểm của hypebol với trục hoành.
Vì A thuộc trục Ox nên toạ độ của A có dạng (xA; 0)
Mà A thuộc hypebol nên
Do đó hypebol cắt trục Ox tại hai điểm A1(–a; 0) và A2(a; 0).
+) Giả sử hypebol cắt trục tung tại B.
Vì B thuộc trục Oy nên toạ độ của B có dạng (0; yB).
Mà B thuộc hypebol nên (vô lí).
Vậy hypebol không cắt trục tung.
c) M(x0; y0) thuộc hypebol nên ta có:
Vì nên====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hypebol x264−y236=1.
a) Tìm tiêu cự và độ dài các trục.
b) Tìm các đỉnh và các đường tiệm cận.
Câu hỏi:
Cho hypebol .
a) Tìm tiêu cự và độ dài các trục.
b) Tìm các đỉnh và các đường tiệm cận.Trả lời:
a) Có a2 = 64, b2 = 36
Do đó, tiêu cự của hypebol là 2c = 20, độ dài trục thực là 2a = 16, độ dài trục ảo là 2b = 12.
b) Các đỉnh của hypebol là A1(–8; 0), A2(8; 0).
Hai đường tiệm cận của hypebol là và====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho điểm M(x0; y0) thuộc hypebol có hai tiêu điểm F1(–c; 0), F2(c; 0), độ dài trục thực bằng 2a.
a) Tính MF12 – MF22.
b) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A2(a; 0), tức là, MF1 – MF2 = 2a. Tính MF1 + MF2, MF1, MF2.
c) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A1(–a; 0), tức là, MF2 – MF1 = 2a. Tính MF1 + MF2, MF1, MF2.
Câu hỏi:
Cho điểm M(x0; y0) thuộc hypebol có hai tiêu điểm F1(–c; 0), F2(c; 0), độ dài trục thực bằng 2a.
a) Tính MF12 – MF22.
b) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A2(a; 0), tức là, MF1 – MF2 = 2a. Tính MF1 + MF2, MF1, MF2.
c) Giả sử M(x0; y0) thuộc nhánh chứa đỉnh A1(–a; 0), tức là, MF2 – MF1 = 2a. Tính MF1 + MF2, MF1, MF2.Trả lời:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 63. Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Câu hỏi:
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6 Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Trả lời:
Hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng 6 2a = 6, 2b = 6
a = 3, b = 3
Theo công thức bán kính qua tiêu ta có:
MF1
MF2====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hypebol x21−y23=1 với hai tiêu điểm F1(–2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
Câu hỏi:
Cho hypebol với hai tiêu điểm F1(–2; 0), F2(2; 0). Điểm M nào thuộc hypebol mà có độ dài bán kính tiêu MF2 nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm.
Trả lời:
Có a2 = 1, b2 = 3
Gọi (x; y) là toạ độ của M.
Theo công thức bán kính qua tiêu ta có: MF2
Nếu M thuộc nhánh bên trái thì x ≤ –a = –1. Khi đó 1 – 2x ≥ 1 – 2(–1) = 3.
Suy ra MF2 = |1 – 2x| ≥ 3.
Nếu M thuộc nhánh bên phải thì x ≥ a = 1. Khi đó 1 – 2x ≤ 1 – 2.1 = –1.
Suy ra MF2 = |1 – 2x| ≥ 1.
Vậy MF2 nhỏ nhất bằng 1 khi x = 1.
Khi đó MF1====== **** mời các bạn xem câu tiếp bên dưới **** =====