Vở bài tập Toán 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác – Cánh diều

By 0

Giải VBT Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

I. Kiến thức trọng tâm

Câu 1 trang 81 vở bài tập Toán lớp 7 Tập 1:

Hình lăng trụ đứng tam giác (Hình 8) có: …. mặt, …. cạnh, ….. đỉnh

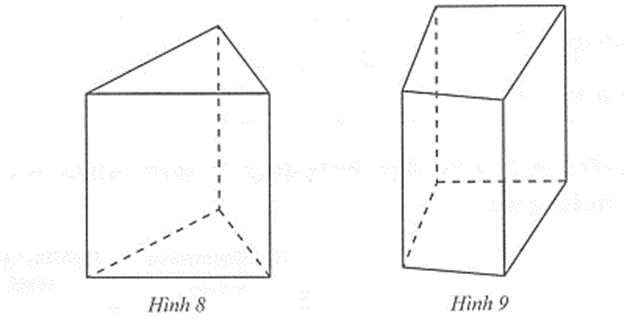
a) Hình lăng trụ đứng tam giác (Hình 8) có: …. mặt, …. cạnh, ….. đỉnh; hai mặt đáy cùng là …………. và …………… với nhau; các mặt bên đều là ………………; các cạnh bên …………….; chiều cao là ………………

– Thể tích của hình lăng trụ đứng tam giác bằng ………………..

– Diện tích xung quanh của hình lăng trụ đứng tam giác bằng …………….

b) Hình lăng trụ đứng tứ giác (Hình 9) có: …. mặt, …. cạnh, ….. đỉnh; hai mặt đáy cùng là …………. và …………… với nhau; các mặt bên đều là ………………; các cạnh bên …………….; chiều cao là ………………

– Thể tích của hình lăng trụ đứng tứ giác bằng ………………………………

– Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng …………….

Lời giải:

a) Hình lăng trụ đứng tam giác (Hình 8) có: 5 mặt, 9 cạnh, 6 đỉnh; hai mặt đáy cùng là tam giác và song song với nhau; các mặt bên đều là hình chữ nhật; các cạnh bên bằng nhau; chiều cao là độ dài một cạnh bên.

– Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

– Diện tích xung quanh của hình lăng trụ đứng tam giác bằng chu vi đáy nhân với chiều cao.

b) Hình lăng trụ đứng tứ giác (Hình 9) có: 6 mặt, 12 cạnh, 8 đỉnh; hai mặt đáy cùng là tứ giác và song song với nhau; các mặt bên đều là hình chữ nhật; các cạnh bên bằng nhau; chiều cao là độ dài một cạnh bên.

– Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

– Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.

II. Luyện tập

  • Câu 1 trang 81 vở bài tập Toán lớp 7 Tập 1: Quan sát Hình 8, Hình 9 và điền số thích hợp vào chỗ chấm (……) trong bảng sau:

    Quan sát Hình 8, Hình 9 và điền số thích hợp vào chỗ chấm (……) trong bảng sau

     

    Hình lăng trụ đứng tam giác

    Hình lăng trụ đứng tứ giác

    Số mặt

    …..

    …..

    Số đỉnh

    …..

    …..

    Số cạnh

    …..

    …..

    Số mặt đáy

    …..

    ……

    Số mặt bên

    …..

    …..

    Lời giải:

     

    Hình lăng trụ đứng tam giác

    Hình lăng trụ đứng tứ giác

    Số mặt

    5

    6

    Số đỉnh

    6

    8

    Số cạnh

    9

    12

    Số mặt đáy

    2

    2

    Số mặt bên

    3

    4

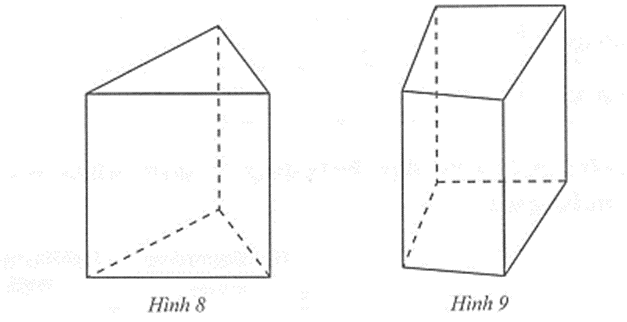
  • Câu 2 trang 82 vở bài tập Toán lớp 7 Tập 1: Quan sát Hình 8, Hình 9 và điền chữ Đ (đúng), S (sai) thích hợp vào chỗ chấm (……) trong bảng sau:

    Quan sát Hình 8, Hình 9 và điền chữ Đ (đúng), S (sai) thích hợp

     

    Hình lăng trụ đứng tam giác

    Hình lăng trụ đứng tứ giác

    Các mặt đáy song song với nhau

    ….

    ….

    Các mặt đáy là tam giác

    ….

    ….

    Các mặt đáy là tứ giác

    ….

    ….

    Các mặt bên là hình chữ nhật

    ….

    ….

    Thể tích bằng diện tích đáy nhân với độ dài cạnh bên

    ….

    ….

    Diện tích xung quang bằng chu vi đáy nhân với độ dài cạnh bên

    ….

    ….

    Lời giải:

     

    Hình lăng trụ đứng tam giác

    Hình lăng trụ đứng tứ giác

    Các mặt đáy song song với nhau.

    Đ

    Đ

    Các mặt đáy là tam giác.

    Đ

    S

    Các mặt đáy là tứ giác.

    S

    Đ

    Mặt bên là hình chữ nhật.

    Đ

    Đ

    Thể tích bằng diện tích đáy nhân với độ dài cạnh bên.

    Đ

    Đ

    Diện tích xung quang bằng chu vi đáy nhân với độ dài cạnh bên.

    Đ

    Đ

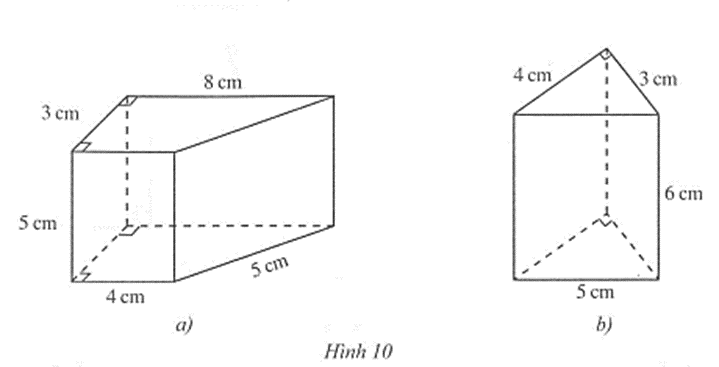
  • Câu 3 trang 82 vở bài tập Toán lớp 7 Tập 1: Cho các hình lăng trụ đứng ở Hình 10a và Hình 10b:

    (i) Hình nào trong các hình 10a, 10b là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?

    (ii) Tính diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác ở Hình 10.

    (iii) Tính thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác ở Hình 10.

    Cho các hình lăng trụ đứng ở Hình 10a và Hình 10b

    Lời giải:

    (i) – Do hình lăng trụ đứng tam giác có: 5 mặt, 9 cạnh, 6 đỉnh; hai mặt đáy cùng là tam giác và song song với nhau nên chỉ có Hình 10b thỏa mãn.

    Vậy trong các hình 10a, 10b thì chỉ có Hình 10b là hình lăng trụ đứng tam giác.

    – Do hình lăng trụ đứng tứ giác có: 6 mặt, 12 cạnh, 8 đỉnh; hai mặt đáy cùng là tứ giác và song song với nhau nên chỉ có Hình 10a thỏa mãn.

    Vậy trong các hình 10a, 10b chỉ có Hình 10a là hình lăng trụ đứng tứ giác.

    (ii) Diện tích xung quanh của:

    + Hình lăng trụ đứng tam giác (Hình 10b) là: (3 + 4 + 5) . 6 = 72 (cm2).

    + Hình lăng trụ đứng tứ giác (Hình 10a) là: (3 + 8 + 5 + 4) . 5 = 100 (cm2).

    (iii) – Ở Hình 10b, hình lăng trụ đứng tam giác có đáy là tam giác vuông.

    Vì thế, thể tích của nó là 12.4.3.6=36 (cm3).

    – Ở Hình 10a, hình lăng trụ đứng tứ giác có đáy là hình thang vuông.

    Vì thế, thể tích của nó là 12.4+8.3.5=90 (cm3).

  • III. Bài tập

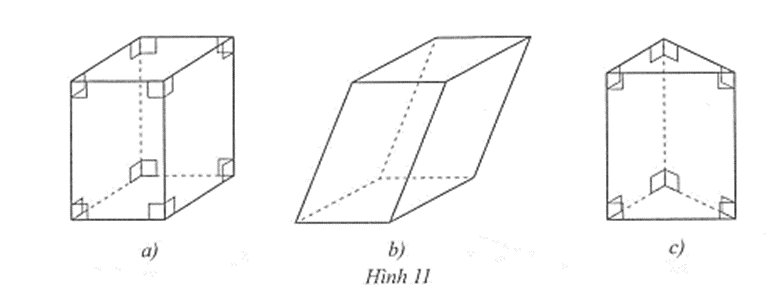
  • Câu 1 trang 84 vở bài tập Toán lớp 7 Tập 1: Trong các hình 11a, 11b, 11c, hình nào là hình lăng trụ đứng tam giác, hình nào là hình lăng trụ đứng tứ giác? Vì sao?

    Trong các hình 11a, 11b, 11c, hình nào là hình lăng trụ đứng tam giác

    Lời giải:

    – Do hình lăng trụ đứng tam giác có: 5 mặt, 9 cạnh, 6 đỉnh; hai mặt đáy cùng là tam giác và song song với nhau; các mặt bên đều là hình chữ nhật nên chỉ có Hình 11c thỏa mãn. Vậy trong các hình đã cho thì chỉ có Hình 11c là hình lăng trụ đứng tam giác.

    – Do hình lăng trụ đứng tứ giác có: 6 mặt, 12 cạnh, 8 đỉnh; hai mặt đáy cùng là tứ giác và song song với nhau; các mặt bên là hình chữ nhật nên chỉ có Hình 11a thỏa mãn. Vậy trong các hình đã cho chỉ có Hình 11a là hình lăng trụ đứng tứ giác.

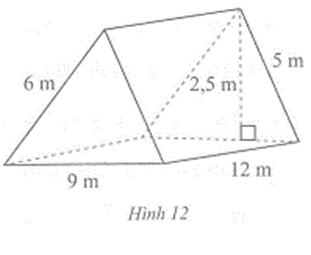
  • Câu 2 trang 84 vở bài tập Toán lớp 7 Tập 1: Trong một chuyến đi dã ngoại bạn Nam đã dựng một lều trại có dạng hình lăng trụ đứng tam giác với các kích thước được mô tả như Hình 12. Tính diện tích vải mà bạn Nam cần để bao kín toàn bộ lều trại đó (phần nền của lều trại đó cũng được phủ bằng vải).

    Trong một chuyến đi dã ngoại bạn Nam đã dựng một lều trại

    Lời giải:

    – Lều trại có dạng một hình lăng trụ đứng với: đáy của lăng trụ đứng này là tam giác có độ dài ba cạnh là 5 m, 6 m, 9 m; chiều cao (độ dài cạnh bên) của lăng trụ đứng này là 12 m. Từ đó, diện tích xung quanh của lều trại hình lăng trụ đứng này là: Sxq = (6 + 5 + 9) . 12 = 240 (m2).

    – Tam giác đáy của lều trại hình lăng trụ đứng này có độ dài một cạnh là 9 m và chiều cao tương ứng là 2,5 m. Từ đó, diện tích một tam giác đáy của lều trại hình lăng trụ đứng này là : Sđ = 12 . 9 . 2,5 = 11,25 (m2).

    – Vậy diện tích vải bạn Nam cần để bao kín toàn bộ lều trại đó (kể cả phần nền) là:

    Sxq + 2.Sđ = 240 + 2 . 11,25 = 262,5 (m2).

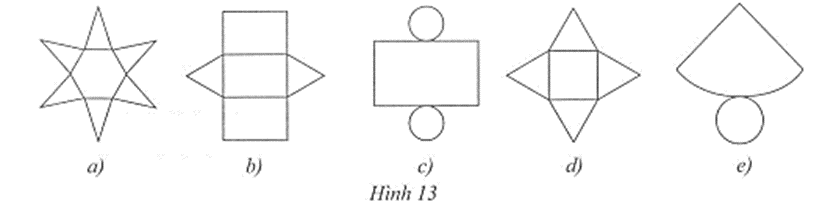
  • Câu 3 trang 85 vở bài tập Toán lớp 7 Tập 1: Quan sát những miếng bìa như ở các hình 13a, 13b, 13c, 13d, 13e và cho biết miếng bìa nào có thể cắt, gấp rồi dán lại để được hình lăng trụ đứng tam giác.

    Quan sát những miếng bìa như ở các hình 13a, 13b, 13c, 13d, 13e

    Lời giải:

    Do hình lăng trụ đứng tam giác có: 5 mặt, 9 cạnh, 6 đỉnh; hai mặt đáy cùng là tam giác và song song với nhau, nên chỉ có miếng bìa ở Hình 13b thỏa mãn. Vì thế, chỉ có miếng bìa ở Hình 13b có thể cắt, gấp rồi dán lại để được hình lăng trụ đứng tam giác.

  • Câu 4 trang 85 vở bài tập Toán lớp 7 Tập 1: Một bể bơi có dạng một hình lăng trụ đứng tứ giác (Hình 14) với: chiều cao AA’ = 12 m; đáy ABCD là một hình thang vuông (nhận AB là đường cao), BC = 0,5 m, AD = 3 m. Biết rằng nếu dùng một máy bơm với công suất là 42 m3/phút thì phải mất 30 phút mới bơm đầy được bể nước này. Tính độ dài AB.

    Một bể bơi có dạng một hình lăng trụ đứng tứ giác (Hình 14)

    Lời giải:

    – Bể bơi có dạng một hình lăng trụ đứng với:

    + Đáy ABCD là một hình thang vuông (nhận AB là đường cao), diện tích nó là:

    S = 0,5+32AB (m2).

    + Chiều cao (hay độ dài cạnh bên) là AA’ = 12 m.

    Từ đó, thể tích của bể bơi có dạng hình lăng trụ đứng đó là:

    V = 0,5+32AB . 12 (m3).

    – Do máy bơm có công suất là 42 m3/phút và bơm 30 phút thì đầy bể nên thể tích của bể là:

    V = 42 . 30 = 1 260 (m3).

    Từ đó, suy ra: 0,5+32AB . 12=1 260 hay 3,52.AB=1260:12 hay 3,52.AB=105

    Do đó, AB = 105 : 3,52 = 60 (m).

    Vậy độ dài AB là 60 m.

Bài liên quan:

Leave a Comment

Back to Top
Menu