Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 2 Toán 7 Kết nối tri thức bản word có lời giải chi tiết ( cho 1 đề thi bất kì):
B1: –
B2: – nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Giữa kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2024 – Đề 1
Phòng Giáo dục và Đào tạo …
Đề thi Giữa kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
I. TRẮC NGHIỆM (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hai đại lượng trong công thức nào tỉ lệ nghịch với nhau:
A. B. C. D.
Câu 2. Biểu thức đại số biểu thị bình phương của một tổng hai số và là:
A. B. C. D.
Câu 3. Giá trị của biểu thức: tại là:
A. B. C. D.
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. B. C. D.
Câu 5. Sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến ta được:
A. B.
C. D.
Câu 6. Cho tam giác có . Độ dài cạnh là một số nguyên (cm). Độ dài cạnh là:
A. B. C. D.
Câu 7. Cho tam giác , có . Khi đó quan hệ giữa ba cạnh là:
A. B. C. D.
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm biết:
a) b)
Bài 2. (1,5 điểm) Ba lớp 7A, 7B, 7C cùng tham gia lao động trồng cây. Biết số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số và hai lần số cây của lớp 7A cộng với lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là cây. Tính số cây trồng được của mỗi lớp
Bài 3. (1,5 điểm) Cho hai đa thức: và .
a) Thu gọn và sắp xếp hai đa thức và theo lũy thừa giảm dần của biến.
b) Tính và tìm nghiệm của đa thức .
Bài 4. (3,5 điểm) Cho tam giác cân tại , kẻ vuông góc với . Gọi là trung điểm của . Trên tia đối của tia lấy điểm sao cho .
a) Chứng minh rằng: và vuông góc với.
b) Chứng minh rằng: từ đó suy ra .
c) Chứng minh rằng:
d) Gọi là trung điểm của . Chứng minh rằng ba điểm thẳng hàng.
Bài 5. (0,5 điểm) Cho các số thực thỏa mãn: .
Chứng minh rằng: .
(Giả thiết các tỉ số đều có nghĩa)
Hướng dẫn giải:
I. Trắc nghiệm
|
1.B |
2. D |
3. A |
4. C |
|
5. A |
6. D |
7. D |
8. C |
Câu 1.
Phương pháp:
Vận dụng định nghĩa về đại lượng tỉ lệ nghịch.
Cách giải:
Ta có: là hai đại lượng tỉ lệ nghịch với nhau.
Chọn B.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Bình phương của một tổng hai số và là:
Chọn D.
Câu 3.
Phương pháp:
Thay vào biểu thức để tính.
Cách giải:
Thay vào biểu thức ta có:
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến:
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là nếu .
+ Trong trường hợp xác định được là số lớn nhất trong ba số thì điều kiện tồn tại tam giác là .
Cách giải:
Xét tam giác , ta có:
Vì độ dài cạnh là một số nguyên nên
Chọn D.
Câu 7.
Phương pháp:
Sử dụng quan hệ giữa góc và cạnh đối diện trong tam giác.
Cách giải:
Xét có: (định lý tổng ba góc trong một tam giác)
Ta có: (vì )
(quan hệ giữa góc và cạnh đối diện trong tam giác)
Chọn D.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp
a) Vận dụng định nghĩa hai phân số bằng nhau: Nếu thì .
b) Phương trình , chia hai trường hợp để giải:
+ Trường hợp 1:
+ Trường hợp 2:
Cách giải:
a)
Vậy
b)
Trường hợp 1:
Trường hợp 2:
Vậy
Câu 2
Phương pháp:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là (cây) (điều kiện: )
Áp dụng tính chất của dãy tỉ số bằng nhau để giải toán.
Cách giải:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là (cây) (điều kiện: )
Vì số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số nên ta có:
Vì hai lần số cây của lớp 7A cộng với lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là cây nên ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Khi đó, (tmđk)
(tmđk)
(tmđk)
Vậy số cây ba lớp trồng được là: Lớp 7A: 18 cây; lớp 7B: 30 cây, lớp 7C: 48 cây.
Bài 3.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức , ta giải phương trình
Cách giải:
a)
b)
Ta có:
Vậy là nghiệm của đa thức
Bài 4.
Phương pháp:
+ Sử dụng các cách chứng minh hai tam giác bằng nhau.
+ Mối quan hệ giữa góc và cạnh trong tam giác (Cạnh đối diện với góc lớn hơn thì lớn hơn)
+ Tính chất trọng tâm của tam giác.
Cách giải:
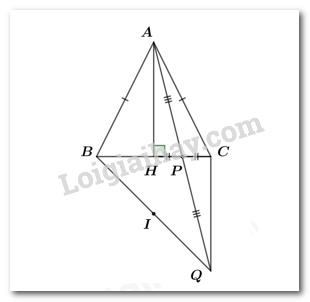
a. Xét và có:
+ (gt)
+ (đối đỉnh)
+ (gt)
(c.g.c) (đpcm).
(hai góc tương ứng)
(đpcm).
b. Theo (a)
(hai cạnh tương ứng) (1)
Mà vuông tại H (cạnh góc vuông <cạnh huyền) (2)
Từ (1) và (2), suy ra (đpcm).
c. Xét có (3) (Mối quan hệ giữa cạnh- góc trong tam giác)
Mặt khác (4)
Từ (3) và (4) hay (đpcm).
d. Xét có là trung tuyến ứng với cạnh
Mà (do là trung điểm của , là trung điểm của ) là trọng tâm (5)
Lại có là trung điểm của là trung tuyến ứng với cạnh (6)
Từ (5), (6)
thẳng hàng (đpcm)
Bài 5.
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: nên
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Mà và (gt) nên (đpcm)
I. TRẮC NGHIỆM (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hai đại lượng trong công thức nào tỉ lệ nghịch với nhau:
A. B. C. D.
Câu 2. Biểu thức đại số biểu thị bình phương của một tổng hai số và là:
A. B. C. D.
Câu 3. Giá trị của biểu thức: tại \(x = – 2\) là:
A. B. C. D.
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. B. C. D.
Câu 5. Sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến ta được:
A. B.
C. \(P\left( x \right) = – 4 – 7{x^2} + 2{x^3} + {x^4}\) D.
Câu 6. Cho tam giác có . Độ dài cạnh là một số nguyên (cm). Độ dài cạnh là:
A. B. C. D.
Câu 7. Cho tam giác , có . Khi đó quan hệ giữa ba cạnh là:
A. Ma trận đề kiểm tra giữa kì 2 môn Toán lớp 7 Kết nối tri thức
Môn: Toán – Lớp 7 – Thời gian làm bài: 90 phút
|
STT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Tổng % điểm |
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TN |
TL |
TN |
TL |
TN |
TL |
TN |
TL |
||||
|
1 |
Tỉ lệ thức và đại lượng tỉ lệ |
Tỉ lệ thức. Tính chất dãy tỉ số bằng nhau |
1 |
|
1 |
2 |
|
1 |
|
1 |
40% |
|
Đại lượng tỉ lệ thuận. Đại lượng tỉ lệ nghịch |
2 |
|
|
|
|
|
|
|
|||
|
2 |
Biểu thức đại số và đa thức một biến |
Biểu thức đại số |
1 |
|
|
|
|
|
|
|
30% |
|
Đa thức một biến |
1 |
|
2 |
2 |
|
|
|
|
|||
|
3 |
Quan hệ giữa các yếu tố trong một tam giác |
Quan hệ giữa góc và cạnh đối diện trong một tam giác |
1 |
|
|
|
|
|
|
|
30% |
|
Quan hệ giữa đường vuông góc và đường xiên |
1 |
|
|
|
|
|
|
|
|||
|
Quan hệ giữa ba cạnh của một tam giác |
|
|
1 |
|
|
|
|
|
|||
|
Sự đồng quy của ba đường trung tuyến trong một tam giác |
1 |
|
|
1 |
|
1 |
|
|
|
||
|
Tổng: Số câu Điểm |
8 (2,0đ) |
|
4 (1,0đ) |
5 (4,0đ) |
|
2 (2,5đ) |
|
1 (0,5đ) |
20 10 |
||
|
Tỉ lệ |
20% |
50% |
25% |
5% |
100% |
||||||
|
Tỉ lệ chung |
70% |
30% |
100% |
||||||||
− Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ điểm được quy định trong ma trận.
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TOÁN – LỚP 7
|
STT |
Nội dung kiến thức |
Đơn vị kiến thức |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ |
|||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||
|
1 |
Tỉ lệ thức và đại lượng tỉ lệ |
Tỉ lệ thức. Tính chất dãy tỉ số bằng nhau |
Nhận biết: – Nhận biết tỉ lệ thức và các tính chất của tỉ lệ thức. – Nhận biết tính chất của dãy tỉ số bằng nhau. – Hiểu rõ định nghĩa, tính chất để lập được tỉ lệ thức. |
1TN |
|
|
|
|
Thông hiểu: Sử dụng tính chất của tỉ lệ thức để tính toán các phép tính đơn giản. |
|
1TN 2TL |
|
|
|||
|
Vận dụng: Vận dụng tính chất của tỉ lệ thức để tính toán các phép tính phức tạp. |
|
|
1TL |
|
|||
|
Vận dụng cao: Chứng minh đẳng thức dựa vào tính chất của tỉ lệ thức và dãy tỉ số bằng nhau. |
|
|
|
1TL |
|||
|
Đại lượng tỉ lệ thuận. Đại lượng tỉ lệ nghịch |
Nhận biết: – Nhận biết hai đại lượng tỉ lệ thuận, đại lượng tỉ lệ nghịch. – Chỉ ra được hệ số tỉ lệ khi biết công thức. |
2TN |
|
|
|
||
|
Vận dụng: Vận dụng được tính chất của đại lượng tỉ lệ thuận, tỉ lệ nghịch để tìm giá trị của một đại lượng và toán chia tỉ lệ. |
|
|
1TL |
|
|||
|
2
|
Biểu thức đại số và đa thức một biến
|
Biểu thức đại số. Đa thức một biến |
Nhận biết: Nhận biết biểu thức số và biểu thức đại số. |
1TN |
|
|
|
|
Phép cộng, phép trừ, phép nhân đa thức một biến |
Nhận biết: – Nhận biết được định nghĩa đa thức một biến. – Nhận biết bậc, hệ số cao nhất, hệ số tự do của một đa thức. – Nhận biết nghiệm của một đa thức. |
1TN |
|
|
|
||
|
Thông hiểu: – Thu gọn và sắp xếp đa thức. – Thực hiện tính toán phép cộng, phép trừ, phép nhân đa thức trong tính toán. – Tính giá trị của một đa thức khi biết giá trị của biến. – Tìm nghiệm của đa thức tổng, hiệu. |
|
2TN 2TL |
|
|
|||
|
3
|
Quan hệ giữa các yếu tố trong một tam giác
|
Quan hệ giữa góc và cạnh đối diện trong một tam giác |
Nhận biết: Nhận biết hai định lý về cạnh và góc đối diện trong tam giác. |
1TN |
|
|
|
|
Quan hệ giữa đường vuông góc và đường xiên |
Nhận biết: – Nhận biết khái niệm đường vuông góc và đường xiên, khoảng cách từ một điểm đến một đường thẳng. – Nhận biết quan hệ giữa đường vuông góc và đường xiên. |
1TN |
|
|
|
||
|
Quan hệ giữa ba cạnh của một tam giác |
Thông hiểu: – Tìm độ dài 3 cạnh bất kì có tạo thành tam giác hay không. – Tìm độ dài một cạnh khi biết độ dài hai cạnh còn lại và các dữ kiện kèm theo. |
|
1TN |
|
|
||
|
Sự đồng quy của ba đường trung tuyến trong một tam giác |
Nhận biết: Nhận biết được đường đường trung tuyến trong tam giác và sự đồng quy của các đường thẳng đó. |
1TN |
|
|
|
||
|
|
|
|
Thông hiểu: Dựa vào tính chất trọng tâm tam giác, tính chất đường trung tính để tìm các tỉ lệ, chứng minh các cạnh bằng nhau. |
|
1TL |
|
|
|
|
|
|
Vận dụng: – Áp dụng tính chất đường trung tuyến, quan hệ giữa ba cạnh của một tam giác để chứng minh đẳng thức, bất đẳng thức. – Tính các tỉ số của các cạnh dựa vào tính chất đường trung tuyến. |
|
|
1TL |
|
Đề thi Giữa kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2024 – Đề 2
Phòng Giáo dục và Đào tạo …
Đề thi Giữa kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Cho . Số vào ô trống để được tỉ lệ thức đúng là
A. 4;
B. −4;
C. 2;
D. 8.
Câu 2. Cho và 4x – y = 42. Khi đó, giá trị của x, y là
A. x = 21, y = 42;
B. x = 42, y = 21;
C. x = −21, y = −42;
D. x = −42, y = −21.
Câu 3. Trong các biểu thức sau, biểu thức nào là đơn thức?
A. 2x – 5;
B. 15x2 – x;
C. 2x2yz2;
D. –10x + 15y.
Câu 4. Hạng tử tự do của biểu thức K(x) = x5 – 4x3 + 2x – 7 là:
A. 2
B. –4;
C. 3;
D. –7.
Câu 5. Kết quả của phép nhân (3x2 + 1)(2x – 5) là đa thức nào trong các đa thức sau?
A. 6x3 + 10x2 − 2x − 5;
B. 6x3 + 10x2 − 2x + 5;
C. 6x3 – 10x2 + 2x − 5;
D. 6x3 – 4x2 + 2x + 5.
Câu 6. Cho hình vuông ABCD, khẳng định nào sau đây là sai ?
A. Đỉnh B cách đều hai điểm A và C;
B. Đỉnh D cách đều hai điểm A và C;
C. Đỉnh A cách đều hai điểm C và B;
D. Đỉnh C cách đều hai điểm D và B.
Câu 7. Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm D nằm giữa A và B (D không trùng với các đỉnh của tam giác ABC). Chọn đáp án đúng nhất.
A. DC > AC > BC;
B. BC > AC > CD;
C. AC > CD > BC;
D. AC < CD < CB.
Câu 8. Một tam giác cân có độ dài hai cạnh 3,9 cm và 7,9 cm. Chu vi của tam giác này là
A. 15,5 cm;
B. 17,8 cm;
C. 19,7 cm;
D. 20,9 cm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Ba bạn An, Hồng và Liên hái được 75 bông hoa để trang trí trại của lớp. Số hoa của An, Hồng và Liên hái được tỉ lệ với các số 4, 5, 6. Tính số hoa mà mỗi bạn đã hái được?
Bài 3. (3,0 điểm) Cho đa thức: M(x) = 6x3 + 2x4 – x2 + 3x2 – 2x3 – x4 + 1 – 4x3.
a) Thu gọn, sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Cho đa thức N(x) = – 5x4 + x3 + 3x2 – 3. Tính M(x) + N(x); M(x) – N(x).
c) Chứng tỏ rằng đa thức M(x) không có nghiệm.
Bài 4. (2,0 điểm) Cho tam giác ABC đều có ba đường trung tuyến AD, BE, CF cắt nhau tại G. Chứng minh:
a) AD = BE = CF.
b) GA = GB = GC.
Bài 5. (0,5 điểm) Cho tỉ lệ thức . Chứng minh rằng .
Đề thi Giữa kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2024 – Đề 3
Phòng Giáo dục và Đào tạo …
Đề thi Giữa kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Cặp tỉ số nào dưới đây lập thành tỉ lệ thức?
A. và ;
B. và ;
C. và ;
D. 1,2 : 2,4 và 4 : 10.
Câu 2. Biểu thức nào dưới đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 3. Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 15. Hệ số tỉ lệ k của y đối với x là
A. 3;
B. 75;
C. ;
D. 10.
Câu 4. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = −3 thì y = 8. Hệ số tỉ lệ là
A. −3;
B. 8;
C. 24;
D. −24.
Câu 5. Trong các biểu thức sau, biểu thức nào là đơn thức?
A. 3x2yz + 2.
B. 3xy3z ;
C. 4x2 – 2x;
D. xy – 7.
Câu 6. là nghiệm của đa thức nào trong các đa thức sau đây?
A. 3x – 4;
B. 3x + 4;
C. 4x – 3;
D. 4x + 3.
Câu 7. Kết quả của phép tính (5x3 + 2x + 1) + (3x2 – 4x +1) là
A. 5x3+ 3x2 – 2x + 2;
B. 5x3 – 3x2 – 2x + 2;
C. 5x3+ 3x2 + 2x + 2;
D. 5x3 – 3x2 – 2x + 2.
Câu 8. Tính (x – 1) . (2x2 – x + 3) = ?
A. x3 + 2x2 + 4x – 3;
B. –x3 – 2x2 + 2x + 3;
C. x3 – 2x2 + 4x – 3;
D. x3 + 2x2 – 4x – 3.
Câu 9. Cho tam giác ABC có BC < AC. Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 10. Trong tam giác ABC có chiều cao AH. Khẳng định nào sau đây là đúng?
A. Nếu BH < HC thì AB < AC;
B. Nếu AB < AC thì BH < HC;
C. Nếu BH = HC thì AB = AC;
D. Cả A, B, C đều đúng.
Câu 11. Cho tam giác ABC biết AB = 1 cm, BC = 9 cm và cạnh AC là một số nguyên. Chu vi tam giác ABC là:
A. 17 cm;
B. 18 cm;
C. 19 cm;
D. 16 cm.
Câu 12. Chọn khẳng định đúng.
A. Điểm đồng quy của ba đường trung tuyến cách mỗi đỉnh của tam giác một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy;
B. Điểm đồng quy của ba đường trung tuyến cách mỗi đỉnh của tam giác một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy;
C. Điểm đồng quy của ba đường trung tuyến cách mỗi đỉnh của tam giác một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy;
D. Điểm đồng quy của ba đường trung tuyến cách mỗi đỉnh của tam giác một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Ba lớp tham gia trồng cây trong vườn trường: số cây trồng được của lớp 7A bằng số cây trồng được của lớp 7B và bằng số cây trồng được của lớp 7C. Biết số cây trồng được của lớp 7C nhiều hơn số cây trồng được của lớp 7A là 28 cây, tính số cây trồng được của mỗi lớp?
Bài 3. (2,0 điểm) Cho hai đa thức: f(x) = x2 – 2x – 5x5 + 7x3 + 12;
g(x) = x3 – 4x4 + 7x2 + 8x – 9.
a) Sắp xếp các đa thức theo luỹ thừa giảm của biến.
b) Tính f(x) + g(x); f(x) – g(x).
Bài 4. (2,0 điểm) Cho tam giác ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Vẽ điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm của BD. Chứng minh:
a) Ba điểm A, G, E thẳng hàng.
b) Đường thẳng DG đi qua trung điểm của AB.
Bài 5. (0,5 điểm) Tìm a, b, c biết: và a – b = 15.
Đề thi Giữa kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2024 – Đề 4
Phòng Giáo dục và Đào tạo …
Đề thi Giữa kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được
A. 50 : 81;
B. 8 : 9;
C. 5 : 8;
D. 1 : 10.
Câu 2. Biết và x + y = −15. Khi đó, giá trị của x, y là
A. x = 6, y = 9;
B. x = −7, y = −8;
C. x = 8, y = 12;
D. x = −6, y = −9.
Câu 3. Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
|
x |
−5 |
1 |
|
y |
1 |
? |
Giá trị cần điền vào “?” là
A. ;
B. ;
C. 5;
D. −5.
Câu 4. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi x = –2 thì y = 4. Khi đó, hệ số a bằng bao nhiêu?
A. –2;
B. –6;
C. –8;
D. – 4.
Câu 5. Các biến trong biểu thức đại số 3x + 2y – 2z là
A. x, z;
B. x, y;
C. x, y, z;
D. y, z.
Câu 6. Bậc của đa thức P = –5x7 + 4x8 – 2x + 1 là
A. 8;
B. 7;
C. 1;
D. 0.
Câu 7. Cho đa thức A = 5x4 – 4x2 + x – 2 và B = x4 + 3x2 – 4x. Tính A + B = ?
A. 6x4 – x2 – 3x;
B. 6x4 – x2 – 3x + 2;
C. 6x4 – x2 + 3x – 2;
D. 6x4 – x2 – 3x – 2.
Câu 8. Tính (–x2) . (2x3 + 3x2 – 2x + 5) = ?
A. –2x5 – 3x4 + 2x3 – 5x2 ;
B. –2x5 – 3x4 + 2x3 + 5x2;
C. –2x5 – 3x4 – 2x3 – 5x2;
D. 2x5 – 3x4 + 2x3 – 5x2.
Câu 9. Chọn khẳng định đúng?
A. Trong một tam giác, góc đối diện với cạnh lớn hơn là góc nhỏ hơn;
B. Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn;
C. Trong một tam giác, góc kề với cạnh lớn hơn là góc lớn hơn;
D. Trong một tam giác, không có quan hệ giữa góc và cạnh đối diện.
Câu 10. Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
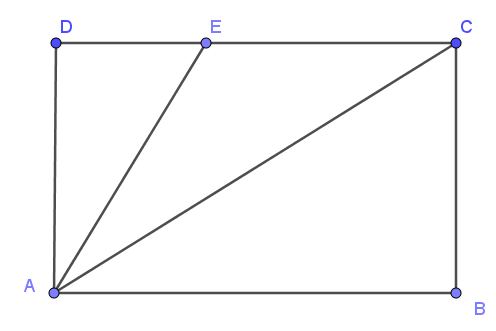
A. AD < AE;
B. AC > AD;
C. AC > AE;
D. AE < AD.
Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
A. 5 cm; 4 cm; 1 cm;
B. 3 cm; 4 cm; 5 cm;
C. 5 cm; 2 cm; 2 cm;
D. 1 cm; 4 cm; 10 cm.
Câu 12. Cho ΔABC nhọn có hai đường trung tuyến AM và BN cắt nhau tại O. Khẳng định nào sau đây sai?
A. ;
B. ;
C. ;
D. .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A: có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Bài 3. (2,0 điểm) Cho hai đa thức: M(x) = 3x4 – 2x3 + 5x2 – 4x + 1;
N(x) = –3x4 + 2x3 –3x2 + 7x + 5.
a) Tính P(x) = M(x) + N(x).
b) Tính giá trị của biểu của P(x) tại x = −2.
Bài 4. (2,0 điểm) Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G. Biết BD = CE.
a) Chứng minh tam giác GBC là tam giác cân.
b) Chứng minh .
Bài 5. (0,5 điểm) Cho tỉ lệ thức . Chứng minh rằng .
Đấp án đề thi Giữa học kì 2 môn Toán lớp 7 Kết nối tri thức – Đề số 4
I. Bảng đáp án trắc nghiệm
|
1. B |
2. D |
3. A |
4. C |
5. C |
6. A |
|
7. D |
8. A |
9. B |
10. D |
11. B |
12. C |
II. Hướng dẫn giải trắc nghiệm
Câu 1.
Ta có .
Câu 2.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Do đó: x = (−3) . 2 = −6; y = (−3) . 3 = −9.
Câu 3.
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ .
Ta có . Do đó giá trị cần điền vào bảng là .
Câu 7.
Ta có A + B = (5x4 – 4x2 + x – 2) + (x4 + 3x2 – 4x)
= (5x4 + x4) + (3x2 – 4x2) + (x – 4x) – 2
= 6x4 – x2 – 3x – 2.
Câu 8.
(–x2) . (2x3 + 3x2 – 2x + 5)
= (–x2) . (2x3) – x2 . 3x2 + x2 . 2x – x2 . 5
= –2x5– 3x4 + 2x3 – 5x2.
Câu 10.
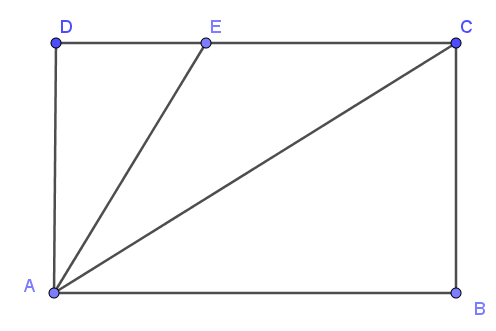
Khẳng định AE < AD là sai vì AD là đường vuông góc, AE là đường xiên.
Câu 11.
Ta có: 5 – 4 = 1 < 3; 5 – 3 = 2 < 4; 4 – 3 = 1 < 5.
Vậy bộ ba độ dài 3 cm; 4 cm; 5 cm có thể tạo thành một tam giác.
Câu 12.
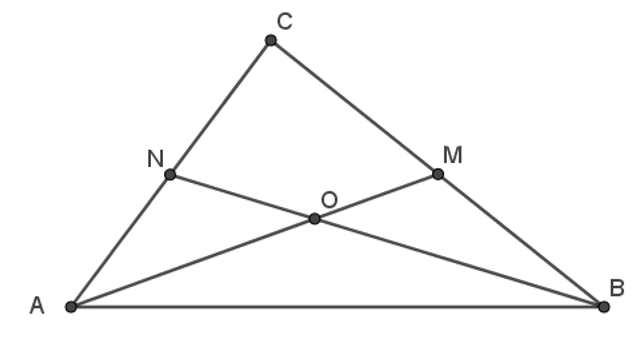
Do hai đường trung tuyến AM và BN cắt nhau tại O nên
; ; ; .
Mà tam giác ABC không cân nên AM ≠ BN nên .
Bài 1. (1,5 điểm)
a)
x = 10
Vậy x = 10.
b)
3x – 7 = 20
3x = 27
x = 9
Vậy x = 9.
c)
x2 = (−4) . (−49)
x2 = 196
x = 14 hoặc x = −14
Vậy x ∈ {14; −14}.
Bài 2. (1,0 điểm)
Gọi x, y, z (tấn) lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0).
Theo đề bài ta suy ra: .
Ba đơn vị cùng vận chuyển 700 tấn hàng nên x + y + z = 700.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó x = 50 . 3,5 = 275; y = 80 . 3,5 = 280; z = 70 . 2,5 = 245 (thỏa mãn).
Vậy đơn vị A, B, C lần lượt vận chuyển được 275 tấn hàng, 280 tấn hàng và 245 tấn hàng.
Bài 3. (2,0 điểm)
a) Ta có P(x) = M(x) + N(x)
= (3x4 – 2x3 + 5x2 – 4x + 1) + (–3x4 + 2x3 – 3x2 + 7x + 5)
= 3x4 – 2x3 + 5x2 – 4x + 1 – 3x4 + 2x3 – 3x2 + 7x + 5
= (3x4 – 3x4) + (– 2x3 + 2x3) +(5x2 – 3x2) + (–4x + 7x ) + (1 + 5)
= 2x2 + 3x + 6.
Vậy P(x) = 2x2 + 3x + 6.
b) Thay x = −2 vào biểu thức P, ta được:
P(–2) = 2 . (–2)2 + 3 . (–2) + 6
= 2 . 4 – 6 + 6 = 8 – 6 + 6 = 8.
Vậy khi x = −2 thì giá trị biểu thức P bằng 8.
Bài 4. (2,0 điểm)
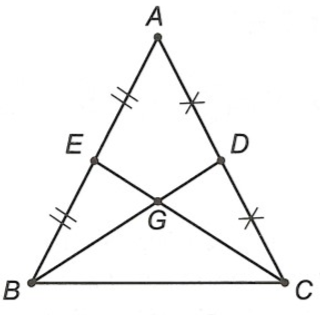
a) Vì hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Suy ra (tính chất trọng tâm của tam giác).
Mà BD = CE (giả thiết) nên .
Vậy tam giác GBC là tam giác cân.
b) Ta có nên suy ra BG = 2DG.
Do đó . (1)
Chứng minh tương tự, ta có: (2)
Từ (1) và (2) suy ra: .
Xét tam giác BCG có BG + CG > BC (trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại).
Vậy (đpcm).
Bài 5. (0,5 điểm)
Vì nên ad = bc.
Ta có: ab(c2 – d2) = abc2 – abd2 = acbc – adbd;
cd(a2 – b2) = cda2 – cdb2 = acad – bcbd.
Do đó ab(c2 – d2) = cd(a2 – b2).
Suy ra (đpcm).
Đề thi Giữa kì 2 Toán lớp 7 Kết nối tri thức có đáp án năm 2024 – Đề 5
Phòng Giáo dục và Đào tạo …
Đề thi Giữa kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là
A. x = −56, y = −32;
B. x = 32, y = 56;
C. x = 56, y = 32;
D. x = 56, y = −32.
Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng:
A. –32;
B. 32;
C. –2;
D. 2.
Câu 5. Biểu thức đại số biểu thị “Bình phương của tổng của hai số x và y” là
A. x2 – y2;
B. x + y;
C. x2 + y2;
D. (x + y)2.
Câu 6. Hệ số tự do của đa thức M = 8x2 – 4x + 3 – x5 là
A. 1;
B. 4;
C. 3;
D. 5.
Câu 7. Cho hai đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9. Giá trị P(x) − G(x) bằng
A. x2 − 9x + 13;
B. 6x3 − 8x2 + 5x − 5;
C. x3 − 8x2 + 5x − 5;
D. 5x3 − 8x2 + 5x + 13.
Câu 8. Kết quả của phép nhân (5x − 2)(2x + 1) là đa thức nào trong các đa thức sau?
A. 10x2 − 3x − 2;
B. 10x2 − x + 4;
C. 10x2 + x − 2;
D. 10x2 − x − 2.
Câu 9. Cho tam giác MNP có: . Khẳng định nào sau đây là đúng ?
A. MP < MN;
B. MP = MN;
C. MP > MN;
D. Không đủ dữ kiện so sánh.
Câu 10. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?
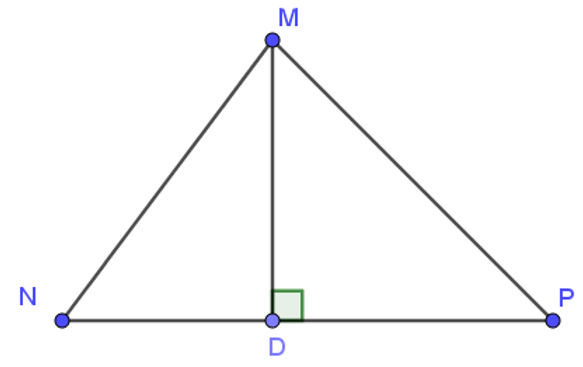
A. DN = DP;
B. MD < MP;
C. MD > MN;
D. MN = MP.
Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 15 cm; 25 cm; 10 cm;
B. 5 cm; 4 cm; 6 cm;
C. 15 cm; 18 cm; 20 cm;
D. 11 cm; 9 cm; 7 cm.
Câu 12. Cho G là trọng tâm tam giác MNP có trung tuyến MK. Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) ;
b) ;
c) .
Bài 2. (1,0 điểm) Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
Bài 3. (2,0 điểm) Cho hai đa thức: P(x) = x3 – 2x2 + x – 2; Q(x) = 2x3 – 4x2 + 3x – 6.
a) Tính P(x) – Q(x).
b) Chứng tỏ rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 4. (2,0 điểm) Cho tam giác ABC có D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK và AC.
a) Chứng minh G là trọng tâm tam giác EFC.
b) Tính các tỉ số .
Bài 5. (0,5 điểm) Cho tỉ lệ thức . Chứng minh rằng .
Đáp án đề thi Giữa học kì 2 môn Toán lớp 7 Kết nối tri thức – Đề số 5
I. Bảng đáp án trắc nghiệm
|
1. C |
2. B |
3. A |
4. A |
5. D |
6. C |
|
7. B |
8. C |
9. C |
10. B |
11. A |
12. B |
II. Hướng dẫn giải trắc nghiệm
Câu 1.
Ta có .
Câu 2.
Ta có 7x = 4y suy ra .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó x = 4 . 8 = 32, y = 7 . 8 = 56.
Câu 7.
Ta có: P(x) − G(x) = (6x3 − 3x2 − 2x + 4) − (5x2 − 7x + 9)
= 6x3 − 3x2 − 2x + 4 − 5x2 + 7x − 9
= 6x3 + (−3x2 − 5x2) + (−2x + 7x) + (4 − 9)
= 6x3 − 8x2 + 5x − 5.
Vậy P(x) − G(x) = 6x3 − 8x2 + 5x −5.
Câu 8.
Ta có: (5x − 2)(2x + 1)
= 5x . (2x + 1) + (−2) . (2x + 1)
= 10x2 + 5x − 4x − 2 = 10x2 + x – 2.
Câu 9.
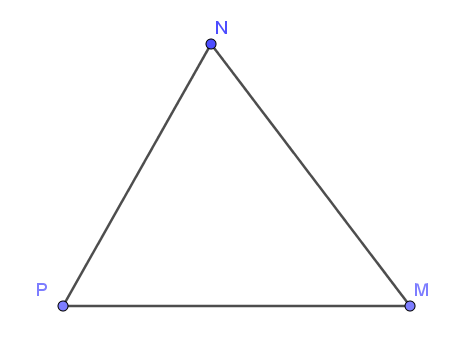
Xét tam giác MNP có suy ra .
Mà cạnh MP là cạnh đối của góc N, MN là cạnh đối của góc P.
Vậy MP > MN.
Câu 11.
Ta thấy 15 = 25 – 10.
Do đó, bộ ba độ dài đoạn thẳng 15 cm; 25 cm; 10 cm không thể tạo thành một tam giác.
Câu 12.
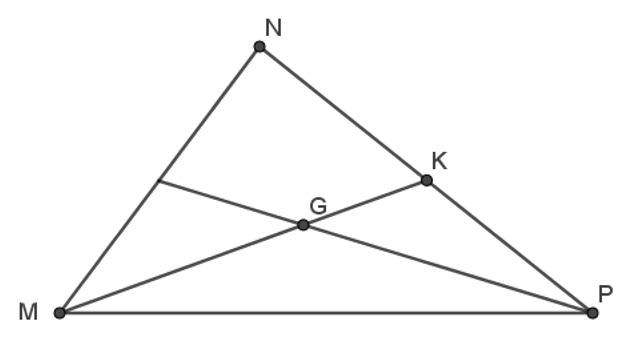
Vì G là trọng tâm tam giác MNP nên G là giao điểm của ba đường trung tuyến nên
.
Mà MG + GK = MK. Do đó .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a)
Vậy .
b)
9x – 1 = 15
9x = 16
Vậy .
c)
3(x + 11) = 2(14 – x)
3x + 33 = 28 – 2x
3x + 2x = 28 – 33
5x = –5
x = –1
Vậy x = –1.
Bài 2. (1,0 điểm)
Trên cùng một quãng đường, vận tốc và thời gian tỉ lệ nghịch với nhau.
Gọi v1, t1 là vận tốc và thời gian của xe I; v2, t2 là vận tốc và thời gian của xe II.
Thời gian xe I đi hết đoạn đường AB là:
14 – 8 = 6 (giờ).
Thời gian xe II đi hết đoạn đường AB là:
(14 – 0,5) – 9 = 4,5 (giờ).
Ta có hay .
Vì vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h nên v2 – v1 = 20.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Suy ra v1 = 20 . 3 = 60; v2 = 20 . 4 = 80.
Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 80 km/h.
Bài 3. (2,0 điểm)
a) Ta có P(x) – Q(x) = (x3 – 2x2 + x – 2) – (2x3 – 4x2 + 3x – 6)
= x3 – 2x2 + x – 2 – 2x3 + 4x2 – 3x + 6
= (x3 – 2x3) + (4x2 – 2x2) + (x – 3x) + (6 – 2)
= – x3 – 2x2 – 2x + 4.
Vậy P(x) – Q(x) = – x3 – 2x2 – 2x + 4.
b) Thay x = 2 vào đa thức P(x), ta có:
P(2) = 23 – 2 . 22 + 2 – 2 = 8 – 2 . 4 + 0 = 8 – 8 = 0;
Thay x = 2 vào đa thức Q(x), ta có:
Q(2) = 2 . 23 – 4 . 22 + 3 . 2 – 6 = 2 . 8 – 4 . 4 + 6 – 6
= 16 – 16 + 0 = 0.
Vậy x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 4. (2,0 điểm)
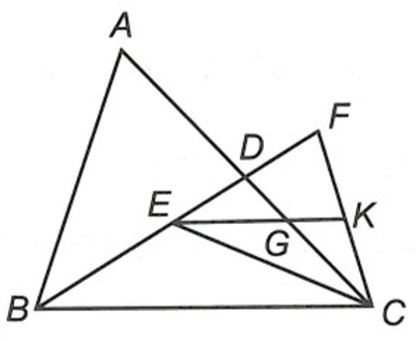
a) Ta có BF = 2BE suy ra BE = EF.
Mà BE = 2ED nên EF = 2ED
Suy ra D là trung điểm của EF
Do đó CD là đường trung tuyến của tam giác EFC.
Vì K là trung điểm của CF nên EK là đường trung tuyến của tam giác EFC.
Tam giác EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của tam giác EFC.
b) Ta có G là trọng tâm của tam giác EFC nên và .
Suy ra nên GE = 2GK.
Do đó .
Bài 5. (0,5 điểm)
Đặt suy ra a = bk, c = dk.
Ta có ;
.
Vậy (đpcm).