Lý thuyết Toán lớp 6 Bài 11: Ước chung. Ước chung lớn nhất
Video giải Toán 6 Bài 11: Ước chung. Ước chung lớn nhất – Kết nối tri thức
A. Lý thuyết Ước chung. Ước chung lớn nhất
1. Ước chung và ước chung lớn nhất
Ước chung của hai hay nhiều số là ước của tất cả các số đó.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
Ta kí hiệu:
ƯC(a, b) là tập hợp các ước chung của a và b.
ƯCLN(a, b) là ước chung lớn nhất của a và b.
Ví dụ 1.
a) Tìm ước chung của 24 và 60.
b) Tìm ƯCLN (24; 60).
Lời giải
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30}
a) ƯC(24; 30) = {1; 2; 3; 6}
b) ƯCLN(24; 30) = 6.
Nhận xét:
– Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.
Nếu a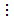 
b thì ƯCLN(a, b) = b.
– Số 1 chỉ có 1 ước là 1. Do đó với mọi số tự nhiên a và b, ta có:
ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.
Ví dụ 2.
a) Tìm ƯCLN(180, 18)
Vì 180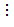 
18 nên ƯCLN(180, 18) = 18.
b) Tìm ƯCLN(13, 1)
Ta có: ƯCLN(13, 1) = 1.
2. Cách tìm ước chung lớn nhất
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
Bước 1: Phân tích các số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Ví dụ 3. Cách tìm ƯCLN(140, 168)
Ta có: 140 = 22.5.7; 168 = 23.3.7.
Các thừa số chung: 2, 7.
Vậy ƯCLN(140, 168) = 22.7 = 4.7 = 28.
3. Rút gọn về phân số tối giản
Vận dụng ƯCLN để rút gọn về phân số tối giản
Ta rút gọn phân số bằng cách chia cả tử và mẫu của phân số đó cho một ước chung khác 1 (nếu có).
Phân số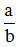 
được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Ví dụ 4. Rút gọn các phân số sau về phân số tối giản
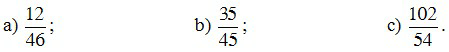
Lời giải
a) ƯCLN(12, 46) = 2.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 12 và 46, ta được:
;
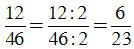b) ƯCLN(35,45) = 5.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 35 và 45, ta được:
;
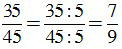c) ƯCLN(102, 54) = 6.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 102 và 54, ta được:
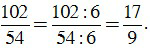
B. Bài tập
Bài 1. Cho hai số a = 132, b = 36.
a) Phân tích a và b ra thừa số nguyên tố.
b) Tìm ƯCLN(a, b) và ƯC(a, b).
Lời giải
a) 132 = 22.3.11; 36 = 22.32.
b) ƯCLN(132, 36) = 22.3 = 12.
ƯC(132, 36) = {1; 2; 3; 4; 6; 12}.
Bài 2. Các phân số sau đã tối giản chưa? Nếu chưa hãy rút gọn phân số đến phân số tối giản.
Lời giải
Tất cả các phân số đã cho đều chưa tối giản.
a) Vì 15050 nên ƯCLN(150, 50) = 50.
Để rút gọn phân số ta chia cả tử và mẫu cho 50, ta được:
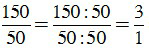= 3
b) Ta có: 90 = 2.32.5, 27 = 33.
ƯCLN(90,27) =32 = 9.
Để rút gọn phân số ta chia cả tử và mẫu cho 9, ta được:
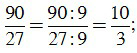
c) Ta có: 34 = 2.17, 255 = 3.5.17.
ƯCLN(34, 255) = 17.
Để rút gọn phân số ta chia cả tử và mẫu cho 17, ta được:
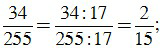
d) Ta có: 88 = 23.11, 121 = 112
ƯCLN(88, 121) = 11.
Để rút gọn phân số ta chia cả tử và mẫu cho 11, ta được:
.
Bài giảng Toán 6 Bài 11: Ước chung. Ước chung lớn nhất – Kết nối tri thức
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 10: Số nguyên tố
Bài 12: Bội chung. Bội chung nhỏ nhất
Chương 2: Tính chia hết trong tập hợp các số tự nhiên
Bài 13: Tập hợp các số nguyên
Bài 14: Phép cộng và phép trừ số nguyên
====== ****&**** =====