Lý thuyết Toán lớp 6 Bài 36: Góc
Video giải Toán 6 Bài 36: Góc – Kết nối tri thức
I. Lý thuyết Góc
1. Góc
– Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.
Ví dụ 1:
+ Góc xOy, kí hiệu 
(hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.
+ Điểm O là đỉnh của góc xOy. Hai tia Ox; Oy là các cạnh của góc xOy.
+ Góc xOy còn có các cách gọi khác là góc AOB; góc O; góc yOx; góc BOA.
+ Đặt biệt khi Ox và Oy là hai tia đối nhau, ta có góc bẹt xOy.
2. Điểm trong của góc
Quan sát hình vẽ:
– Ta gọi M là một điểm trong của góc xOy (điểm M nằm trong góc xOy).
– Các điểm nằm trên hai cạnh của góc và các điểm như điểm N không phải là điểm trong góc xOy.
II. Bài tập vận dụng
Bài 1: Quan sát hình vẽ và kể tên các điểm nằm trong góc xOy?
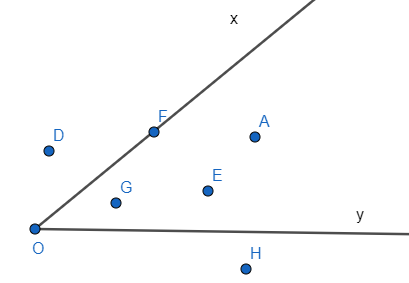
Lời giải:
Các điểm nằm trong góc xOy là: G; E; A.
Bài 2: Kể tên các góc đỉnh E và đỉnh D có trong hình; viết tên bằng kí hiệu của các góc đó và cho biết cạnh của góc.
Lời giải:
– Góc đỉnh E là góc DEF
Viết tên theo kí hiệu là ∠DEF
Cạnh của góc ∠DEF là ED và EF.
– Góc đỉnh D gồm các góc: góc EDF; góc EDC; góc FDC
+ Góc EDF
Viết tên theo kí hiệu là ∠EDF
Cạnh của góc là cạnh DE và cạnh DF.
+ Góc EDC
Viết tên theo kí hiệu là ∠EDC
Cạnh của góc là cạnh DE và cạnh DC.
+ Góc FDC
Viết tên theo kí hiệu là ∠FDC
Cạnh của góc là cạnh DF và cạnh DC.
Bài 3: Cho hình vẽ:
a) Kể tên các góc có trong hình?
b) Kể tên các cạnh của các góc đó?
c) Nêu mối quan hệ về cạnh của hai góc bất kỳ.
Lời giải:
a) Các góc có trong hình là: ∠xOy;∠yOz;∠zOx
b) Các cạnh của góc ∠xOy là Ox và Oy.
Các cạnh của góc ∠yOz là Oy và Oz.
Các cạnh của góc ∠zOx là Ox và Oz.
c) Hai góc ∠xOy và ∠yOz có cạnh chung là Oy.
Hai góc ∠yOz và ∠zOx có cạnh chung là Oz.
Hai góc ∠zOx và ∠xOy có cạnh chung là Ox.
Bài giảng Toán 6 Bài 36: Góc – Kết nối tri thức
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 35: Trung điểm của đoạn thẳng
Bài 37: Số đo góc
Chương 8: Những hình học cơ bản
Bài 38: Dữ liệu và thu thập dữ liệu
Bài 39: Bảng thống kê và biểu đồ tranh
====== ****&**** =====