Lý thuyết Toán lớp 6 Bài 10: Số nguyên tố
Video giải Toán 6 Bài 10: Số nguyên tố – Kết nối tri thức
A. Lý thuyết Số nguyên tố
1. Số nguyên tố và hợp số
– Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
– Hợp số là số tự nhiên lơn hơn 1, có nhiều hơn hai ước.
Ví dụ 1. Trong các số đã cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
190; 11; 132; 23; 43; 17; 21.
Lời giải
Ta thấy 190 có các ước là 1, 2, 5, 190 nhiều hơn hai ước nên 190 là hợp số;
11 chỉ có ước là 1 và 11 nên 11 là số nguyên tố;
132 có các ước là 1; 2; 132 nhiều hơn hai ước nên 132 là hợp số;
23 chỉ có ước là 1 và 23 nên 23 là số nguyên tố;
43 chỉ có ước là 1 và 43 nên 43 là số nguyên tố;
17 chỉ có ước là 1 và 17 nên 17 là số nguyên tố;
21 có các ước là 1; 3; 7; 21 nhiều hơn hai ước nên 21 là hợp số.
2. Phân tích một số ra thừa số nguyên tố
Mọi số đều có thể phân tích ra tích của các thừa số nguyên tố
Cách phân tích một số ra thừa số nguyên tố:
+) Phương pháp phân tích bằng sơ đồ cây
Ví dụ 2. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cây:
Lời giải
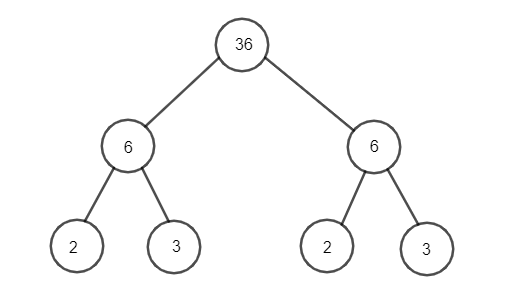
Vậy 36 = 22.32.
+) Phương pháp phân tích bằng sơ đồ cột
Ví dụ 3. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cột:
|
36
18
9
3
1
|
2
2
3
3
|
Vậy 36 = 22.32.
B. Bài tập
Bài 1. Phân tích các số sau ra thừa số nguyên tố: 60; 121; 225.
Lời giải
Ta sẽ sử dụng sơ đồ cột
|
60
30
15
5
1
|
2
2
3
5
|
Vậy 60 = 22.3.5
Vậy 121 = 112
Vậy 225 = 32.52
Bài 2. Các khẳng định sau đúng hay sai? Vì sao?
a) Ước nguyên tố của 12 là 1; 2; 3.
b) Tích hai số nguyên tố bất kì luôn là số chẵn.
c) Mọi số chẵn đều là hợp số.
d) Mọi số lẻ đều là số nguyên tố.
Lời giải
a) 1; 2; 3 là các ước của 12, trong đó 2 và 3 là số nguyên tố còn 1 không phải là số nguyên tố nên a sai.
b) Ta có 3 và 5 là hai số nguyên tố. Tích 3.5 = 15 không phải là số chẵn. Do đó b sai.
c) Số 2 là số chẵn nhưng 2 là số nguyên tố nên c sai.
d) Ta có 15 là số lẻ nhưng 15 không phải là số nguyên tố. Do đó d sai.
Bài giảng Toán 6 Bài 10: Số nguyên tố – Kết nối tri thức
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 9: Quan hệ chia hết và tính chất
Bài 11: Ước chung. Ước chung lớn nhất
Bài 12: Bội chung. Bội chung nhỏ nhất
Chương 2: Tính chia hết trong tập hợp các số tự nhiên
Bài 13: Tập hợp các số nguyên
====== ****&**** =====