Với tóm tắt lý thuyết Toán lớp 10 Bài 3: Tích của một số với một vectơ sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Bài 3: Tích của một số với một vectơ
A. Lý thuyết Tích của một số với một vectơ
1. Tích của một số với một vectơ và các tính chất
Cho số k ≠ 0 và . Tích của số k với là một vectơ, kí hiệu là .
Vectơ cùng hướng với nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng .
Ta quy ước và .
Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.
Ví dụ: Cho tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, BC, CA. Tìm các vectơ bằng: .
Hướng dẫn giải
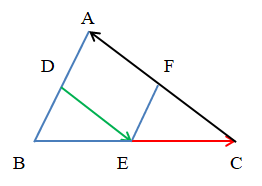
+ Vectơ bằng :
Tam giác ABC có D, E lần lượt là trung điểm của AB, BC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // AC và 2DE = AC.
Vì k = 2 > 0 nên vectơ cần tìm cùng hướng với và có độ dài bằng 2DE.
Ta có cùng hướng với và 2DE = AC.
Do đó .
+ Vectơ bằng :
Ta có F là trung điểm CA.
Do đó FA = CF = .
Vì k = < 0, nên vectơ cần tìm ngược hướng với và có độ dài bằng .
Ta có ngược hướng với và AF = FC = .
Do đó .
+ Vectơ bằng :
Ta có E là trung điểm BC.
Do đó CB = 2EC.
Vì k = –2 < 0, nên vectơ cần tìm ngược hướng với và có độ dài bằng 2EC.
Ta có ngược hướng với và CB = 2EC.
Do đó .
Tính chất:
Với hai vectơ và bất kì, với mọi số thực h và k, ta có:
+) ;
+) ;
+) ;
+) ;
+) .
Ví dụ: Ta có:
a) ;
b) ;
c) ;
d) .
Ví dụ: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi .
Hướng dẫn giải
Ta có
(quy tắc ba điểm)
⇔ G là trọng tâm của tam giác ABC (đpcm).
2. Điều kiện để hai vectơ cùng phương
Hai vectơ và () cùng phương khi và chỉ khi có số k sao cho .
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k ≠ 0 để .
Chú ý: Cho hai vectơ và không cùng phương. Với mỗi luôn tồn tại duy nhất cặp số thực (m; n) sao cho .
Ví dụ: Cho tam giác ABC. Lấy các điểm M, N, P sao cho , , .
a) Biểu diễn theo .
b) Biểu diễn theo .
c) Chứng minh rằng: 3 điểm M, N, P thẳng hàng.
Hướng dẫn giải
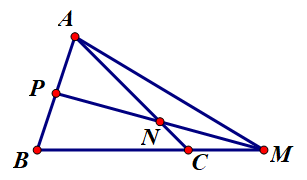
a) Ta có .
Mà cùng hướng (do k = 3 > 0)
Do đó ba điểm B, C, M thẳng hàng và C nằm giữa B, M sao cho MB = 3MC.
Ta có nên P là trung điểm AB.
Do đó AP = AB.
Mà cùng hướng.
Suy ra .
Ta có:
Ta có
.
Ta có
Vậy (1)
b) Ta có .
Do đó hay NA = 3NC.
Khi đó ta có AN = AC.
Mà ngược hướng (do k = ‒3 < 0).
Do đó ba điểm A, N, C thẳng hàng và N nằm giữa hai điểm A và C sao cho
Suy ra .
Ta có
Vậy (2)
c) Từ (1), ta suy ra .
Từ (2), ta suy ra .
Do đó ta có hay .
Vậy ba điểm M, N, P thẳng hàng.
B. Bài tập tự luyện
Bài 1. Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng .
Hướng dẫn giải
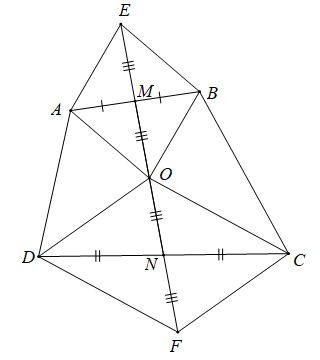 Gọi E và F lần lượt là điểm đối xứng với O qua M và N.
Gọi E và F lần lượt là điểm đối xứng với O qua M và N.
Suy ra M là trung điểm của AB và EO; N là trung điểm của DC và OF.
Khi đó các tứ giác OAEB và OCFD là các hình bình hành
(quy tắc hình bình hành trong hình bình hành OAEB)
Và (quy tắc hình bình hành trong hình bình hành OCFD).
Vì O là trung điểm của MN nên OM = ON, mà OM = ME, ON = MF.
Do đó OE = OF hay O là trung điểm của EF
Suy ra .
Bài 2. Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị theo hai vecto và
Hướng dẫn giải
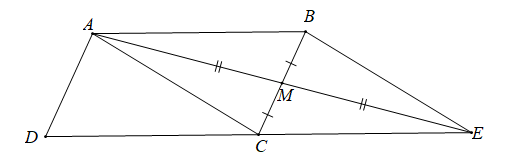
Gọi E là điểm đối xứng với A qua M.
Khi đó M là trung điểm của BC và AE.
Suy ra tứ giác ABEC là hình bình hành.
(quy tắc hình bình hành)
Mà (M là trung điểm của AE)
Xét hình bình hành ABCD có: (quy tắc hình bình hành)
Vậy
Bài 3. Cho tam giác ABC.
a) Hãy xác định điểm M để
b) Chứng minh rằng với mọi điểm O, ta có:
Hướng dẫn giải
a) Gọi G là trọng tâm tam giác ABC suy ra .
Ta có:
(vì )
Do đó vecto cùng hướng với vecto và
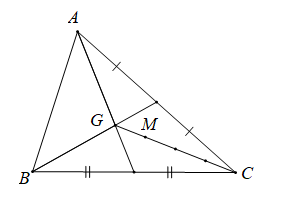
Vậy điểm M nằm giữa G và C sao cho
b) Ta có:
(vì )
Vậy với mọi điểm O, ta có:
====== ****&**** =====