b) Gọi K là trung điểm OM. Chứng minh NK // (SBC)

By 0

Câu hỏi:

b) Gọi K là trung điểm OM. Chứng minh NK // (SBC)

Trả lời:

b) Ta có OMN // SBCNK⊂OMN⇒NK // SBC.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của ΔABC, ΔACD, ΔABD. Chứng minh rằng MNP // BCD.

    Câu hỏi:

    Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của ΔABC, ΔACD, ΔABD.
    Chứng minh rằng MNP // BCD.

    Trả lời:

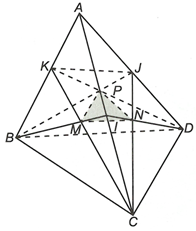
    Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của ABC, ACD, ABD . Chứng minh rằng (MNP) // (BCD) (ảnh 1)

    Gọi I, J, K lần lượt là trung điểm AC, AD, AB.
    Xét ΔIBD có IMIB=INID=13 nên MN // BD.
    Suy ra MN // BCD.
    Xét ΔJBCcó IMIB=INID=13 nên NP // BC.
    Suy ra NP // BCD.
    Ta có MN // BCDNP // BCDMN,NP⊂MNP,MN∩NP=N
    ⇒MNP // BCD.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC.a) Chứng minh (MNP) // (ABCD)

    Câu hỏi:

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC.
    a) Chứng minh (MNP) // (ABCD)

    Trả lời:

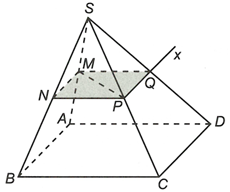
    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC. a) Chứng minh (MNP) // (ABCD) (ảnh 1)

    a) Ta có MN // AB, AB⊂ABCD⇒MN // ABCD.
    Tương tự NP // BC, BC⊂ABCD⇒NP // ABCD.
    Ta có MN // ABCDNP // ABCDMN,NP⊂MNP,MN∩NP=N⇒MNP // ABCD.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. b) Gọi Q là giao điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.

    Câu hỏi:

    b) Gọi Q là giao điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.

    Trả lời:

    b) Ta có SD⊂SCD.
    Xét hai mặt phẳng MNP và SCD có P∈MNP∩SCD
    Ta có CD⊂SCD,MN⊂MNPMN // CD⇒MNP∩SCD=Px
    sao cho Px // CD // MN.(vì MN // AB theo tính chất đường trung bình và CD // AB)
    Trong SCD gọi Px∩CD=Q.Suy ra MNP∩CD=Q.
    Ta có MNP∩SCD=PQ nên PQ // CD // MN suy ra Q là trung điểm của SD và MN=12AB=12CD=PQ.
     
    Vậy tứ giác MNPQ là hình bình hành (cặp cạnh đối song song và bằng nhau).

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của A’B’ và AB. Chứng minh (AMC’) // (CNB’)

    Câu hỏi:

    Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của A’B’ và AB. Chứng minh (AMC’) // (CNB’)

    Trả lời:

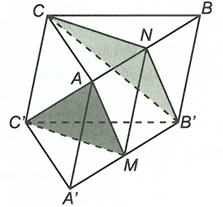
    Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của A'B' và AB. Chứng minh (AMC') // (CNB') (ảnh 1)

    Ta có MN // AA‘,AA‘ // CC‘⇒MN // CC‘ và theo tính chất hình lăng trụ thì MN=CC‘ nên tứ giác MNCC‘ là hình bình hành và CN // MC‘.
    CN // MC‘MC‘⊂AMC‘⇒CN // AMC‘.
    Mặt khác AN // B‘M,AN=B‘M nên tứ giác ANB‘M là hình bình hành và NB‘ // MA.
    Ta có NB‘ // MAMA⊂AMC‘⇒NB‘ // AMC‘.
    Lại có CN // AMC‘NB‘ // AMC‘CN,NB‘⊂CNB‘CN∩NB‘=N⇒AMC‘ // CNB‘.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Cho hình lập phương ABCD.A’B’C’D’, có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD’. Chứng minh rằng (MNP) song song với (ACD’)

    Câu hỏi:

    Cho hình lập phương ABCD.A’B’C’D’, có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD’. Chứng minh rằng (MNP) song song với (ACD’)

    Trả lời:

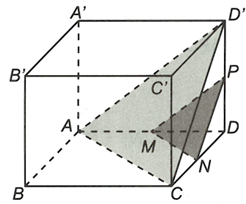
    Cho hình lập phương ABCD.A'B'C'D', có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD'. Chứng minh rằng (MNP) song song với (ACD') (ảnh 1)
    Xét ΔADD‘ có MP // AD‘, mà AD‘⊂ACD‘⇒MP // ACD‘.
    Tương tự trong ΔACD có MN // AC, mà AC⊂ACD‘⇒MN // ACD‘
    Ta có MP // ACD‘MN // ACD‘MN,MP⊂MNPMN∩MP=M.
    Suy ra MNP // ACD‘.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu