Bộ 40 đề thi học kì 2 Toán 8 có đáp án năm 2023

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chỉ 150k mua trọn bộ Đề thi học kì 2 Toán 8 bản word có lời giải chi tiết:

B1:   –

B2:   – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Bộ Đề thi Toán lớp 8 Học kì 2 năm 2022 – 2023 – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 1:

Bài 1 (2,5điểm). Giải các phương trình:

a) $2x–7=5x+20$                                      b) $x^3-4x=0$

c) $\frac{1}{2x-3}-\frac{3}{2x^2-3x}=\frac{5}{x}$                              d) $\left|x^2-1\right|=2x+1$

Bài 2 (1,5 điểm). Giải các bất phương trình:

a) $3x-5 \le x+1$               b) $\frac{2x-2}{3}>2-\frac{x+2}{2}$

Bài 3 (1,5 điểm). 

Một ôtô đi từ thành phố Hồ Chí Minh đến Phan Thiết với vận tốc 60km/h. Khi trở về cũng trên tuyến đường đó, ôtô chạy với vận tốc 40km/h nên thời gian về mất nhiều hơn thời gian đi là 2 giờ 10 phút. Tính quãng đường từ thành phố Hồ Chí Minh đến Phan Thiết?

Bài 4 (3,5 điểm).

1) Cho hình chữ nhật ABCD. Kẻ AH $\perp$ BD (H $\in$ BD).

a) Chứng minh: $\Delta HDA$ đồng dạng với $\Delta ADB$

b) Chứng minh: AD² = DB.HD

c) Tia phân giác của góc ADB cắt AH và AB lần lượt tại M và K. Chứng minh: $AK.AM=BK.HM$

  d) Gọi O là giao điểm của AC và BD. Lấy P thuộc AC, dựng hình chữ nhật AEPF

(E$\in$AB, F$\in$AD). BF cắt DE ở Q. Chứng minh rằng: EF//DB và 3 điểm A, Q, O thẳng hàng.

2) Tính thể tích hình hộp chữ  nhật ABCD.EFGH biết cạnh AE = 5cm; EH = 4cm; AB = 3cm.

Bài 5 (1 điểm).

a) Cho các số a, b, c thỏa mãn: a + b + c = $\frac{3}{2}$. Chứng minh rằng: a² + b² + c² $\ge \frac{3}{4}$

b) Tìm giá trị nhỏ nhất của biểu thức P = x² + 2y² + 2xy – 6x – 8y + 2028.

………………………………………………………………………

Bộ Đề thi Toán lớp 8 Học kì 2 năm 2022 – 2023 – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

 

Đề 2:

Phần I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm):

          Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy làm bài. Ví dụ câu 1 chọn đáp án C thì ghi là 1C.

Câu 1: Phương trình $x=3$ tương đương với phương trình nào sau đây?

A. $2x=-6$.

B. $2x=6$.

C. $x=-3$.

D. $-2x=6$.

Câu 2: Điều kiện xác định của phương trình $\frac{2}{x}+\frac{1}{x-6}=3$  là

A. $x\ne 0$ và $x\ne 6$.

B. $x\ne 6$.

C. $x\ne 0$.

D. $x\ne 0$ và $x\ne -6$.

Câu 3: Phương trình $\left(\text{2x}-\text{5}\right).\left(\text{x}-\text{7}\right)=0$ có tập hợp nghiệm là

A. $S=\left\{-\frac{5}{2};7\right\}$.

B. $S=\left\{\frac{5}{2};7\right\}$.

C. $S=\left\{\frac{2}{5};7\right\}$.

D. $S=\left\{\frac{-5}{2};-7\right\}$.

Câu 4: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?

A. $x+\frac{2}{3}\le 0$.

B. $0x+\frac{1}{2}>0$..

C. $x^2>\frac{1}{4}$.

D. $\frac{1}{x}+2<0$.

Câu 5: Bất phương trình $2x-4>0$ có nghiệm là

A. $x>4$.

B. $x>-4$.

C. $x>-2$.

D. $x>2$.

Câu 6: Rút gọn biểu thức $A=\left|3-x\right|+5x-8$ khi $x<3$ ta được A bằng

A. $4x-5$.

B. $4x-11$.

C. $6x-11$.

D. $6x-5$.

Câu 7: Mẹ cho Hiếu số tiền vừa đủ mua 4 gói bánh, giá 5000 đồng mỗi gói. Hiếu gặp một Tổ chức từ thiện đang quyên góp nhằm ủng hộ đồng bào bị lũ lụt. Hiếu quyết định ủng hộ x% số tiền mình đang có (x < 100). Biểu thức nào sau đây biểu thị số tiền Hiếu còn lại để đi mua bánh?

A. $20000-\frac{x}{5}$.

B. $20000-200x$.

C. $20-\frac{x}{5}$.

D. $20-\frac{x}{100}$.

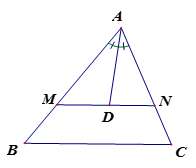
*Quan sát hình 1 và thực hiện các câu hỏi:  8;  9; 10.

Biết MN//BC; AD là đường phân giác của tam giác AMN; AM = 6cm; MB = 3cm; BC =9cm.

Câu 8: Tỉ số $\frac{DN}{DM}$ bằng tỉ số

A. $\frac{DN}{DM}$. C. $\frac{AM}{AN}$.

B. $\frac{AM}{DN}$. D. $\frac{AN}{AM}$.

Câu 9: Tỉ số $\frac{AN}{NC}$ bằng tỉ số

A. $\frac{AM}{AB}$.

B. $\frac{AN}{NC}$.

C. $\frac{AM}{MB}$.

D. $\frac{MN}{BC}$.

 

Câu 10: Độ dài đoạn thẳng MN là

A. $4,5cm$.

B. $6dm$.

C. $6cm$.

D. $3cm$.

*Quan sát hình 2 và thực hiện các câu hỏi: 11; 12; 13; 14.

 Biết  là hình hộp chữ nhật có

  AB = 4cm; BC = 6cm; = 5cm.

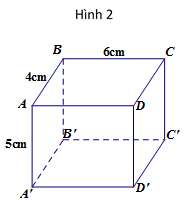
Câu 11: Đường thẳng CD song song với đường thẳng   

A. AA’. C. AB.

B. DD’. D. B’C’.

Câu 12: Đường thẳng CC’ song song với mặt phẳng

A. $\left(AA‘B‘B\right)$. C. $\left(A‘B‘C‘D‘\right).$

B. $\left(AA‘C‘C\right)$. D. $\left(ABCD\right).$

Câu 13: Mặt phẳng $\left(CC‘D‘D\right)$ vuông góc với mặt phẳng

A. $\left(AA‘B‘B\right).$

B. $\left(A‘B‘C‘D‘\right).$

C. $\left(BB‘D‘D\right).$

D. $\left(AA‘C‘C\right).$

Câu 14: Một hộp thủy tinh dạng hình hộp chữ nhật, trong lòng có các kích thước như hình 2 thì có thể chứa tối đa bao nhiêu lít nước?

A. 120 lít

B. 12 lít.

C. 0,12 lít.

D. 1,2 lít.

Câu 15: Hình lập phương có diện tích toàn phần là 294cm² thì có thể tích là

A. $343c{m}^3.$

B. $49c{m}^3.$

C. $294c{m}^3.$

D. $2401c{m}^3.$

Phần II. TỰ LUẬN (5,0 điểm):

Câu 1. (1,5 điểm)

a.      Giải phương trình sau: $4x-2=3x-5.$

b.     Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: $4x-1<8.$

Câu 2. (1,0 điểm)

a.      Cho biết $x>y,$ chứng tỏ rằng $-5x-2019<-5y-2019$.

b.     Giải phương trình sau: $\frac{x-2003}{16}+\frac{x-1997}{11}+\frac{x-1992}{9}+\frac{x-1991}{7}=10.$

Câu 3. (2,5 điểm)

Cho tam giác nhọn DEF, hai đường cao EM và FN cắt nhau tại I.

a. Chứng minh hai tam giác DME và DNF đồng dạng;

b. Chứng minh $IM.IE=IN.\text{\hspace{0.17em}IF}$;

c.      Cho biết $\widehat{EDF}={45}^0$. Chứng tỏ rằng ${\left(\frac{MN}{\text{EF}}\right)}^2=\frac{1}{2}.$

………………………………………………………………………

Bộ Đề thi Toán lớp 8 Học kì 2 năm 2022 – 2023 – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 3:

Bài 1 (1,0 điểm) :

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Đường thẳng AA’ vuông góc với các mặt phẳng nào?

Bài 2 (3,0 điểm) : Giải các phương trình sau:

Bài 3 (2,0 điểm) : Một người đi xe máy từ A đến B hết 2 giờ và từ B về A hết 1 giờ 48 phút. Tính vận tốc của xe máy lúc đi từ A đến B, biết vận tốc lúc về lớn hơn vận tốc lúc đi là 4km/h.

 

Bài 4 (3,0 điểm) : Cho tam giác ABC vuông tại A, đường cao AH.

a) Chứng minh ΔABC ∼ ΔHBA.

b) Chứng minh AB² = BH.BC.

c) Tia phân giá của góc ABC cắt AH, AC theo thứ tự tại M và N.

Chứng minh  .

Bài 5 (1,0 điểm) : Tìm tất cả các cặp số (x; y) thỏa mãn:

2010x² + 2011y² – 4020x + 4022y + 4021 = 0

………………………………………………………………………

Bộ Đề thi Toán lớp 8 Học kì 2 năm 2022 – 2023 – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 4:

Bài 1 (2,5 điểm) : Giải phương trình và bất phương trình sau:

Bài 2 (2,5 điểm) :

Cho biểu thức  (ĐKXĐ:  )

a) Rút gọn A

b) Tìm các giá trị của x để 

Bài 3 (2,0 điểm) : Giải bài toán bằng cách lập phương trình

Một đội thợ mỏ lập kế hoạch khai thác than, theo đó mỗi ngày phải khai thác 40 tấn than. Nhưng khi thực hiện, mỗi ngày đội khai thác được 45 tấn than. Do đó đội đã hoàn thành kế hoạch trước 2 ngày và còn vượt mức 10 tấn than. Hỏi theo kế hoạch đội phải khai thác bao nhiêu tấn than.

Bài 4 (4,5 điểm) : Cho hình chữ nhật ABCD có AD = 6cm; AB = 8cm; hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng d vuông góc với BD, d cắt tia BC tại E.

a) Chứng minh rằng: ΔBDE đồng dạng với ΔDCE

b) Kẻ CH ⊥ DE tại H. Chứng minh rằng: DC² = CH.DB

c) Gọi K là giao điểm của OE và HC. Chứng minh K là trung điểm của HC và tính tỉ số diện tích của ΔEHC và diện tích của ΔEDB

Bài 5 (0,5 điểm) : Cho tích a.b.c = 1 và 

Chứng minh rằng: (a – 1)(b – 1)(c – 1) > 0

Trường THCS Nghĩa Tân

Đề kiểm tra học kì II

Môn Toán – Lớp 8

Thời gian: 90 phút

I. Trắc nghiệm khách quan (1 điểm)
Em hãy chọn chữ cái đứng trước câu trả lời đúng:

Câu 1: Điều kiện xác định của phương trình \(\frac{1}{{(x + 3)(x – 2)}} = \frac{5}{{{x^2} – 4}}\)là:

A. \(x \ne  – 3\)và \(x \ne 2\)

B. \(x \ne  \pm 3\)và \(x \ne 2\)

C. \(x \ne  – 3,x \ne 4\)và\(x \ne 2\)

D. \(x \ne  – 3\)và \(x \ne  \pm 2\)

Câu 2. Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?

A. 2x > 4

B. 1 – 2x > – 3

C. 2x -1\( \ge 3\)

D. \(5 – 3x \le  – 1\)

Câu 3. Cho tam giác ABC vuông tại A có AB = 8cm, BC = 10 cm. AD là phân giác của góc A (D thuộc cạnh BC), khi đó \(\frac{{BD}}{{CD}}\)là:

A. \(\frac{3}{4}\)

B. \(\frac{3}{5}\)

C. \(\frac{4}{3}\)

D. \(\frac{5}{3}\)

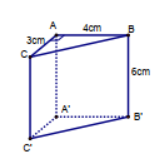
Câu 4. Cho hình lăng trụ đứng ABC.A’B’C’ có ∆ABC vuông tại A, AB = 4cm, AC = 3cm, BB’ = 6cm. Diện tích xung quanh của hình lăng trụ đó là:

A. 360cm²

B. 72 cm²

C. 36 cm²

D. 24 cm²

II. BÀI TẬP TỰ LUẬN (9 điểm)
Bài 1. (2 điểm).

Cho biểu thức \(P = (\frac{{15 – x}}{{{x^2} – 25}} + \frac{2}{{x + 5}}):\frac{{x + 1}}{{2{x^2} – 10x}}\)( với \(x \ne 0;x \ne  – 1;x \ne  \pm 5\))

a) Chứng minh \(P = \frac{{2x}}{{x + 1}}\)

b) Tính giá trị của biểu thức P biết |2x – 3|=7.

c) Tìm x nguyên để P nhận giá trị nguyên.

Bài 2. ( 1,5 điểm) Giải bài toán bằng cách lập phương trình:
Một tổ sản xuất theo kế hoạch mỗi ngày phải làm được 18 sản phẩm. Nhưng thực tế do cải tiến kĩ thuật, mỗi ngày tổ đã làm được thêm 4 sản phẩm nên đã hoàn thành công việc trước 3 ngày và còn vượt mức 14 sản phẩm. Tính số sản phẩm tổ đó phải làm theo kế hoạch.
Bài 3. ( 1,5 điểm) Giải các phương trình và bất phương trình sau:
a) (2x – 1)(x+7) =x² – 49

b) \(\frac{{2x + 1}}{{x – 3}} – \frac{x}{{x + 3}} = 1\)

c) \(\frac{{x + 2}}{3} – \frac{{3x – 1}}{5} <  – 2\)

Bài 4. ( 3,5 điểm)

Cho tam giác MNP vuông tại M, đường cao MH .

a) Chứng minh ∆HNM đồng dạng với \(\Delta MNP\)

b) Chứng minh hệ thức MH² = NH. PH

c) Lấy điểm E tùy ý trên cạnh MP( E khác M; P) , vẽ điểm F trên cạnh MN sao cho \(\widehat {FHE} = {90^o}\), EF cắt MH tại điểm I. Chứng minh \(\Delta NFH\) đồng dạng với \(\Delta MEH\) và \(\widehat {FMI} = \widehat {FEH}\)

d) Xác định vị trí của điểm E trên MP sao cho diện tích ∆HEF đạt giá trị nhỏ nhất.
Bài 5. (0,5 điểm) Cho x > 1; y > 1 và x + y = 6. Tìm giá trị nhỏ nhất của : 

\(S = 3x + 4y + \frac{5}{{x – 1}} + \frac{9}{{y – 1}}\)

——– Hết ——–

Chú ý: • Học sinh được sử dụng máy tính bỏ túi.

• Giám thị coi thi không giải thích gì thêm.

• Chúc các em làm bài tốt!

Biểu điểm chấm và đáp án đề thi học kỳ 2

Môn Toán 8

I. Trắc nghiệm khách quan: (1 điểm): Mỗi câu đúng được 0,25 điểm

Câu 1	Câu 2	Câu 3	Câu 4
D	B	C	B

II. Bài tập tự luận (9 điểm):

Bài 1(2 điểm)

a) Biến đổi được: \(P = \frac{{15 – x + 2x – 10}}{{(x – 5)(x + 5)}}:\frac{{x + 1}}{{2x(x – 5)}}\) \( = \frac{{x + 5}}{{(x – 5)(x + 5)}}.\frac{{2x(x – 5)}}{{x + 1}}\) \(P = \frac{{2x}}{{x + 1}}\)	0.5đ   0.25đ   0.25đ
b) Lập luận tìm được \(\left[ \begin{array}{l}x = 5(loai)\\x =  – 2(chon)\end{array} \right.\) Thay x= – 2 tính được P =4	0.25đ   0.25đ
c) Biến đổi  \(P = 2 – \frac{2}{{x + 1}}\) Vì x nguyên nên P nguyên khi \(\frac{2}{{x + 1}}\)có giá trị nguyên \( \Leftrightarrow 2 \vdots (x + 1)\) Tìm được \(x \in {\rm{\{ }}1; – 2;3\} \)	0.25đ     0.25đ

 

Bài 2: (1.5 điểm) Giải toán bằng cách lập phương trình:

Gọi số sản phẩm tổ đó phải làm theo kế hoạch là x (sản phẩm)( \(x \in  \in {\mathbb{N}^*}\)) Thời gian tổ đó hoàn thành công việc theo kế hoạch là \(\frac{x}{{18}}\)(ngày). Năng suất thực tế của tổ là 18 + 4 = 22 (sản phẩm/ngày). Số sản phẩm tổ đó làm được thực tế là x + 14 (sản phẩm). Thời gian thực tế tổ làm xong x + 14 sản phẩm là \(\frac{{x + 14}}{{22}}\)(ngày)  Vì tổ hoàn thành công việc trước 3 ngày nên ta có pt; \(\frac{x}{8} – \frac{{x + 14}}{{22}} = 3\) Tìm được x = 360 Đối chiếu kq và trả lời                                                        \[\]

0.25đ               0.75đ 0.25đ 0.25đ

Bài 3. (1,5 điểm) Giải các phương trình và bất phương trình sau:

a) (2x – 1)(x +7) = x2 – 49 Biến đổi được về pt (x+7)(x+6)=0 Tìm được S = { – 6; – 7}	0.25đ 0.25đ
b) \(\frac{{2x + 1}}{{x – 3}} – \frac{x}{{x + 3}} = 1\) Tìm đkxđ và biến đổi được pt thành 10x + 12 = 0 Tìm được \(S = {\rm{\{ }}\frac{{ – 6}}{5}{\rm{\} }}\) Chú ý: HS không tìm ĐKXĐ và đối chiếu với ĐKXĐ thì trừ 0,25đ	0.25đ 0.25đ
c) \(\frac{{x + 2}}{3} – \frac{{3x – 1}}{5} <  – 2\) Biến đổi được bpt -4x<-43 tìm được \(x > \frac{{43}}{4}\)	0.25đ 0.25đ

 

Bài 4 ( 3,5 điểm)

Hình vẽ đúng đến câu a)   a) Chứng minh được \(\Delta HNM\~\Delta MNP\)(g-g)	0.25đ             0.75đ
b) Từ câu a) suy ra\(\widehat {HMN} = \widehat {MPN}\)hay \(\widehat {HMN} = \widehat {MPH}\) Chứng minh được \(\Delta HNM\)~\(\Delta HMP\)(g-g) Từ đó suy ra MH2 = NH. HP	0.25đ 0.5đ 0.25đ
c) Chứng minh \(\widehat {NHF} = \widehat {MHE}\)(cùng phụ với góc FHM) chứng minh \(\Delta NFH\)~\(\Delta MEH\)(g-g) suy ra \(\frac{{NH}}{{MH}} = \frac{{HF}}{{HE}} \Rightarrow \frac{{NH}}{{NF}} = \frac{{MH}}{{HE}}\) Chứng minh \(\Delta HEF\)~\(\Delta HMN\)(c-g-c) Suy ra \(\widehat {NMH} = \widehat {FEH}\)hay \(\widehat {FMI} = \widehat {FEH}\)( đpcm)	0.25đ 0.25đ     0.25đ 0.25đ
d) Vì \(\Delta HEF\~\Delta HMN\)(cmt) nên tỉ số đồng dạng \(k = \frac{{HE}}{{MH}}\) suy ra \(\frac{{{S_{HEF}}}}{{{S_{HMN}}}} = {k^2} = {(\frac{{HE}}{{MH}})^2} = \frac{{H{E^2}}}{{M{H^2}}}\) \({S_{HEF}} = \frac{{H{E^2}}}{{M{H^2}}}.{S_{HMN}}\) Mà MH và SHMN không đổi, vậy diện tích của tam giác HEF đạt GTNN khi HE nhỏ nhất \( \Leftrightarrow HE \bot MP\) Vậy diện tích tam giác HEF đạt GTNN khi E là hình chiếu của H lên cạnh MP.	0.25đ       0.25đ

 

Bài 5. (0.5 điểm)

\(S = 3x + 4y + \frac{5}{{x – 1}} + \frac{9}{{y – 1}}\) \( = {\rm{[}}\frac{5}{4}(x – 1) + \frac{5}{{x – 1}}{\rm{] + [}}\frac{9}{4}(y – 1) + \frac{9}{{y – 1}}{\rm{]}} + \frac{7}{4}(x + y) + \frac{7}{2}\)	0.25đ
Áp dụng bdt Cosi cho các cặp số dương có : \(S \ge 2.\frac{5}{2} + 2.\frac{9}{2} + \frac{7}{4}.6 + \frac{7}{2} = 28\) Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x + y = 6\\\frac{5}{4}(x – 1) = \frac{5}{{x – 1}}\\\frac{9}{4}(y – 1) = \frac{9}{{y – 1}}\\x;y > 1\end{array} \right. \Leftrightarrow x = y = 3\) Vậy GTNN của S là 28 khi x = y = 3	0.25đ