Giải bài tập Toán lớp 8 Bài 8: Diện tích xung quanh của hình chóp đều
Trả lời câu hỏi giữa bài
Câu hỏi 1 trang 119 Toán 8 Tập 2: Vẽ, cắt và gấp miếng bìa như ở hình 123. Quan sát hình gấp được, hãy điền số thích hợp vào chỗ trống (…) ở các câu dưới đây:
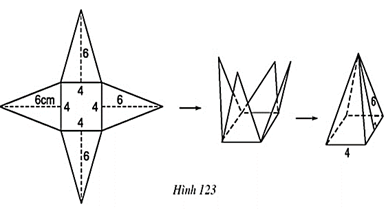
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là …
b) Diện tích mỗi mặt tam giác là … cm2.
c) Diện tích đáy của hình chóp đều là … cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là … cm2.
Lời giải:
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là . 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.
Bài tập (trang 121)
Bài 40 trang 121 Toán 8 Tập 2: Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích toàn phần của hình chóp.
Lời giải:
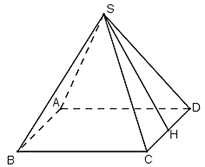
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)
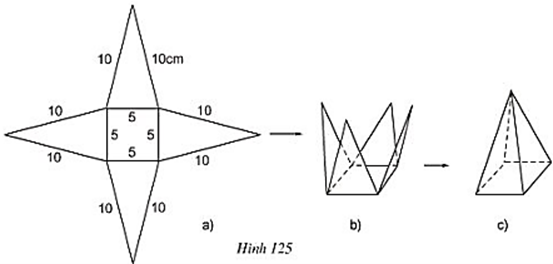
Bài 41 trang 121 Toán 8 Tập 2: Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
b) Sử dụng định lí Pi – ta – go để tính chiều cao ứng với đáy của mỗi tam giác.
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?
Lời giải:
a) Trong hình 125a có 4 tam giác cân bằng nhau.
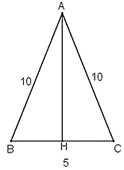
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
Ta có:
Chiều cao ứng với đáy của mỗi tam giác:
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
Diện tích đáy:
Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq
= 25 + 25 121,8 (cm2)
Bài 42 trang 121 Toán 8 Tập 2: Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125.
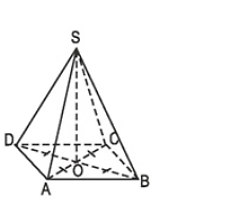
Lời giải:
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Py – ta – go vào tam giác ABC ta được
AC2 = AB2 + BC2 = 52 + 52 = 50
cm
Do O là trung điểm của AC nên:
Tam giác SAO vuông tại O nên:
SO2 = SA2 – AO2
Vậy độ dài đường cao của hình chóp là .
Bài 43 trang 121 Toán 8 Tập 2: Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).
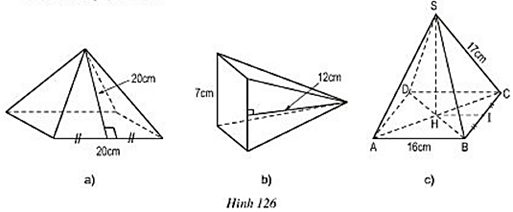
Lời giải:
Diện tích xung quanh:
Hình a:
(trong đó chu vi đáy là 20.4 cm)
Diện tích đáy: Sd = 202 = 400 (cm2)
Diện tích toàn phần:
Stp = Sxq + Sđ = 800 + 400 = 1200 (cm2)
Hình b:
Chu vi đáy là 4.7 = 28 (cm)
Diện tích xung quanh là:
Sd = 72 = 49 cm2
Stp = 168 + 49 = 217 cm2
Hình c:
+) Diện tích đáy là Sd = 162 = 256 (cm2 ).
Do I là trung điểm của BC nên
.
+) Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao.
Ta có:
+) Chu vi đáy là: 16 .4 = 64 (cm)
+) Diện tích xung quanh là:
.
+) Diện tích toàn phần là:
Stp = Sđ + Sxq = 256 + 480 = 736 (cm2).