50 Bài tập Phương trình chứa ẩn ở mẫu (có đáp án)- Toán 8

Bài tập Toán 8 Chương 3 Bài 5: Phương trình chứa ẩn ở mẫu

A. Bài tập Phương trình chứa ẩn ở mẫu

I. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình là?

   A. x = – 1.   B. x = – $\frac{1}{56}$.

   C. x = 1.   D. x = $\frac{1}{56}$

Lời giải:

+ ĐKXĐ: x ≠ – 7; x ≠ $\frac{3}{2}$.

Ta có:

⇒ (3x – 2)(2x – 3) = (6x + 1)(x + 7)

⇔ 6x² – 13x + 6 = 6x² + 43x + 7

⇔ 56x = – 1 ⇔ x = – $\frac{1}{56}$.

Vậy phương trình đã cho có nghiệm x = – $\frac{1}{56}$.

Chọn đáp án B.

Bài 2: Nghiệm của phương trình $\frac{\left(x+1\right)}{(3–x)}$ = 2 là?

A. x = – $\frac{5}{3}$.   

B. x = 0.

C. x = $\frac{5}{3}$.   

D. x = 3.

Lời giải:

+ ĐKXĐ: x ≠ 3.

+ Ta có: $\frac{\left(x+1\right)}{3–x}$= 2 ⇒ x + 1 = 2(3 – x)

⇔ x + 1 = 6 – 2x ⇔ 3x = 5 ⇔ x = $\frac{5}{3}$.

Vậy phương trình có nghiệm là x = $\frac{5}{3}$.

Chọn đáp án C.

Bài 3: Tập nghiệm của phương trình là?

A. S = { ± 1 }.   

B. S = { 0;1 }.

C. S = { 1 }.   

D. S = { Ø }.

Lời giải:

+ ĐKXĐ: x² – 1 ≠ 0 ⇒ x ≠ ± 1.

+ Ta có:

⇒ (x + 1)² – (x – 1)² = 4

⇔ x² + 2x + 1 – x² + 2x – 1 = 4

⇔ 4x = 4 ⇔ x = 1.

So sánh điều kiện, ta thấy x = 1 không thỏa mãn.

Vậy phương trình đã cho có tập nghiệm là S = { Ø }.

Chọn đáp án D.

Bài 4: Nghiệm của phương trình là?

   A. x = $\frac{5}{3}$.   B. x = – $\frac{5}{3}$.

   C. x = – 2.   D. x = 2.

Lời giải:

+ ĐKXĐ: ⇔ x ≠ 0, x ≠ – 5.

+ Ta có:

⇒ (2x² + 15x + 25) – 2x² = 0

⇔ 15x + 25 = 0 ⇔ x = – $\frac{5}{3}$.

Vậy phương trình đã cho có nghiệm là x = – $\frac{5}{3}$.

Chọn đáp án B.

Bài 5: Giá trị của m để phương trình $\frac{\left(x–m\right)}{(x+2)}$ = 2 có nghiệm x = – 3 là ?

A. m = 0.   

B. m = 1.

C. m = – 1.   

D. m = 2.

Lời giải:

+ Điều kiện: x ≠ – 2.

+ Phương trình có nghiệm x = – 3, khi đó ta có: $\frac{( – 3 – m)}{( – 3 + 2)}$ = 2

⇔ $\frac{( – m – 3)}{( – 1)}$ = 2

⇔ m + 3 = 2 ⇔ m = – 1.

Vậy m = – 1 là giá trị cần tìm.

Chọn đáp án C.

Bài 6: Tìm nghiệm của phương trình sau:

   A. x = 0     B. x = -2

   C. x = 3     D. x = 1

Lời giải:

Kết hợp điều kiện thì nghiệm của phương trình đã cho là x = 1

Chọn đáp án D

Bài 7: Giải phương trình sau:

A. x = -2    

B. x = 1

C. x = 3    

D. x = -3

Lời giải:

Điều kiện xác định: x ≠ 2; x ≠ -1

Kết hợp điều kiện, vậy nghiệm phương trình đã cho là x = – 3

Chọn đáp án D

Bài 8: Cho phương trình sau. Tìm điều kiện xác định của phương trình trên?

Lời giải:

Chọn đáp án B

Bài 9: Tìm các giá trị của x để biểu thức sau có giá trị bằng 2:

Lời giải:

Điều kiện: 

Để biểu thức đã cho có giá trị bằng 2 thì:

Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = $\frac{5}{3}$

Chọn đáp án A

Bài 10: Giải phương trình sau:

Lời giải:

Kết hợp điều kiện ta được nghiệm của phương trình đã cho là x = -1 và

x = –$\frac{1}{2}$

Chọn đáp án C

II. Bài tập tự luận có lời giải

Bài 1: Phương trình  có số nghiệm là?

Lời giải

ĐKXĐ: x ≠ 1; x ≠ 2

Vậy phương trình có một nghiệm x = 3

Bài 2 Phương trình  có số nghiệm là?

Lời giải

Điều kiện: x ≠ -1

Vậy phương trình có nghiệm duy nhất

Bài 3 Cho phương trình .

Bạn Long giải phương trình như sau:

Bước 3: ⇒ x – 2 – 7x + 7 = -1 ⇔ -6x = -6 ⇔ x = 1

Vậy tập nghiệm của phương trình là S = {1}

Bạn Long giải sai từ bước nào?

Lời giải

Vậy phương trình vô nghiệm

Bạn Long sai ở bước 3 do không đối chiếu với điều kiện ban đầu

Bài 5 Cho hai biểu thức: . Tìm x sao cho A = B.

Lời giải

Vậy để A = B thì x = 0 hoặc x = 1

Bài 6 Giải các phương trình:

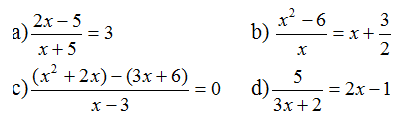
Lời giải:

a) Điều kiện xác định: x ≠ -5.

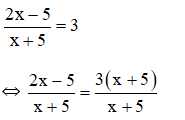
2x – 5 = 3(x + 5)

⇔ 2x – 5 = 3x + 15

⇔ -5 – 15 = 3x – 2x

⇔ x = -20 (thỏa mãn điều kiện xác định).

Vậy phương trình có tập nghiệm S = {-20}.

b) Điều kiện xác định: x ≠ 0.

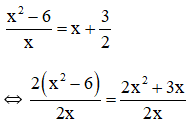
2(x² – 6) = 2x² + 3x

⇔ 2x² – 12 – 2x² – 3x = 0

⇔ 3x = 12

⇔ x = 4 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {4}.

c) Điều kiện xác định: x ≠ 3.

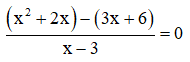
⇔ x² + 2x – (3x + 6) = 0

⇔ x(x + 2) – 3(x + 2) = 0

⇔ (x – 3)(x + 2) = 0

⇔ x – 3 = 0 hoặc x + 2 = 0

+ x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ)

+ x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-2}.

d) Điều kiện xác định: x ≠ –$\frac{2}{3}$.

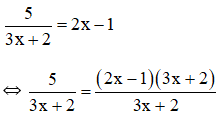
⇔ 5 = (2x – 1)(3x + 2)

⇔ 2x.3x – 3x.1 + 2x.2 – 2.1 = 5

⇔ 6x² – 3x + 4x – 2 = 5

⇔ 6x² + x – 7 = 0.

⇔ 6x² – 6x + 7x – 7 = 0

(Tách để phân tích vế trái thành nhân tử)

⇔ 6x(x – 1) + 7(x – 1) = 0

⇔ (6x + 7)(x – 1) = 0

⇔ 6x + 7 = 0 hoặc x – 1 = 0

+ 6x + 7 = 0 ⇔ 6x = – 7 ⇔ x = –$\frac{7}{6}$ (thỏa mãn đkxđ)

+ x – 1 = 0 ⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm:

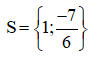
Bài 8 Giải các phương trình:

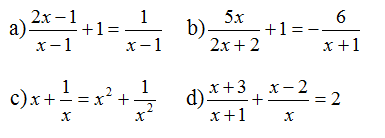
Lời giải:

a) Điều kiện xác định: x ≠ 1.

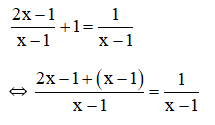
⇔ 2x – 1 + x – 1 = 1

⇔ 3x – 2 = 1

⇔ 3x = 3

⇔ x = 1 (không thỏa mãn điều kiện xác định).

Vậy phương trình vô nghiệm.

b) Điều kiện xác định: x ≠ -1.

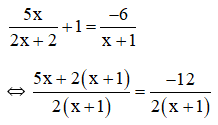
⇔ 5x + 2x + 2 = -12

⇔ 7x + 2 = -12

⇔ 7x = -14

⇔ x = -2 (thỏa mãn đkxđ)

Vậy phương trình có tập nghiệm S = {-2}

c) Điều kiện xác định: x ≠ 0.

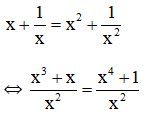
⇔ x³ + x = x⁴ + 1

⇔ x⁴ + 1 – x – x³ = 0

⇔ (x⁴ – x³) + (1 – x) = 0

⇔ x³(x – 1) – (x – 1) = 0

⇔ (x³ – 1)(x – 1) = 0

⇔ (x – 1)(x² + x + 1)(x – 1) = 0

⇔ x – 1 = 0 (vì x² + x + 1 = (x + $\frac{1}{2}$)2 + $\frac{3}{4}$ > 0 với mọi x).

⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {1}.

d) Điều kiện xác định: x ≠ 0 và x ≠ -1.

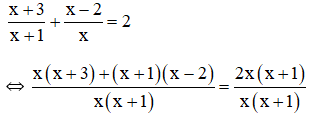
⇔ x(x + 3) + (x + 1)(x – 2) = 2.x(x + 1)

⇔ x(x + 3) + (x + 1)(x – 2) – 2x(x + 1) = 0

⇔ x² + 3x + x² + x – 2x – 2 – (2x² + 2x) = 0

⇔ x² + x² – 2x² + 3x + x – 2x – 2x – 2 = 0

⇔ 0x – 2 = 0

Bài 9 Giá trị x = 1 có phải là nghiệm của phương trình hay không ? Vì sao ?

Lời giải

Giá trị x = 1 không phải là nghiệm của phương trình.

Vì tại x = 1 thì 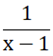  có mẫu bằng 0, không thỏa mãn

Bài 10 Tìm điều kiện xác định của mỗi phương trình sau:

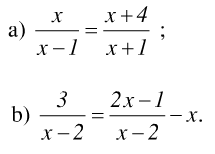
Lời giải

a) Phương trình  xác định :

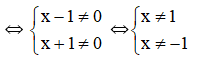
Vậy ĐKXĐ của phương trình là x ≠ ±1.

b) x – 2 ≠ 0 khi x ≠ 2

Vậy ĐKXĐ của phương trình là x ≠ 2.

III. Bài tập vận dụng

Bài 1 Giải các phương trình:

a. $\frac{2x-5}{x+5}=3$

b. $\frac{x^2-6}{x}=x+\frac{3}{2}$

c. $\frac{(x^2+2x)-(3x+6)}{x-3}=0$

d. $\frac{5}{3x+2}=2x-1$

Bài 2 Giải các phương trình:

a. $\frac{2x-1}{x-1}+1=\frac{1}{x-1}$

b. $\frac{5x}{2x+2}+1=-\frac{6}{x+1}$

c. $x+\frac{1}{x}=x^2+\frac{1}{x^2}$

d. $\frac{x+3}{x+1}+\frac{x-2}{x}=2$

Bài 3 Bạn Sơn giải phương trình $\frac{x^2-5x}{x-5}=5(1)$như sau:

$(1)\iff x^2-5x=5(x-5)$

$\iff x^2-5x=5x-25)$

$\iff x^2-10x+25=0)$

$\iff (x-5{)}^2=0)$

$\iff x=5)$

Bài 4 Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức $x-5$ có chứa ẩn. Hà giải bằng cách rút gọn vế trái như sau:

$(1)\iff \frac{x(x-5)}{x-5}=5\iff x=5$

Hãy cho biết ý kiến của em về hai lời giải trên.

Bài 5 Giải các phương trình:

a. $\frac{1}{x-2}+3=\frac{x-3}{2-x}$

b. $2x-\frac{2x^2}{x+3}=\frac{4x}{x+3}+\frac{2}{7}$

c. $\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{x^2-1}$

d. $\frac{3x-2}{x+7}=\frac{6x+1}{2x-3}$

Bài 6 Giải các phương trình:

a) $\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}$

b) $\frac{3}{\left(x-1\right)\left(x-2\right)}+\frac{2}{\left(x-3\right)\left(x-1\right)}=\frac{1}{\left(x-2\right)\left(x-3\right)}$

c) $1+\frac{1}{x+2}=\frac{12}{8+x^3}$

d) $\frac{13}{\left(x-3\right)\left(2x+7\right)}+\frac{1}{2x+7}=\frac{6}{\left(x-3\right)\left(x+3\right)}$

Bài 7 Giải các phương trình:

a) $\frac{1}{x}+2=\left(\frac{1}{x}+2\right)\left(x^2+1\right)$

b) ${\left(x+1+\frac{1}{x}\right)}^2={\left(x-1-\frac{1}{x}\right)}^2$

Bài 8 Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2:

a) $\frac{3a-1}{3a+1}+\frac{a-3}{a+3}$

b) $\frac{10}{3}-\frac{3a-1}{4a+12}-\frac{7a+2}{6a+18}$

Bài 9 Giải các phương trình:

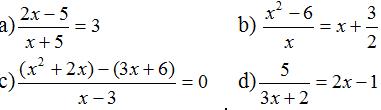
Bài 10 Giá trị x = 1 có phải là nghiệm của phương trình hay không? Vì sao?

Bài 11 Tìm điều kiện xác định của mỗi phương trình sau:

 

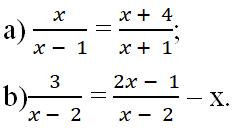
B. Lý thuyết Phương trình chứa ẩn ở mẫu

1. Lưu ý

Khi giải phương trình chứa ẩn ở mẫu, ta cần đặc biệt chú ý đến điều kiện xác định (ĐKXĐ) là tất cả các mẫu thức phải khác 0.

2. Cách giải phương trình chứa ẩn ở mẫu

Bước 1. Tìm ĐKXĐ của phương trình.

Bước 2. Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3. Giải phương trình vừa nhận được.

Bước 4. Kiểm tra và kết luận.