50 Bài tập Diện tích đa giác (có đáp án)- Toán 8

Bài tập Toán 8 Chương 2 Bài 6: Diện tích đa giác

A. Bài tập Diện tích đa giác

I. Bài tập tự luận

Bài 1.

Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình ABCDE (h.152).

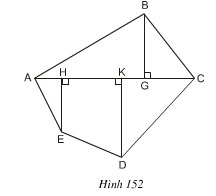
bai-37

Giải:

Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.

Thực hiện phép đo chính xác đến mm ta được:

BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm

KC = 22mm, EH = 16mm, KD = 23mm

Nên S_ABC= 1/2.BG. AC = 1/2. 19.48 = 456 (mm²)

S_AHE= 1/2 AH. HE = 1/2. 8.16 = 64 (mm²)

S_DKC= 1/2 KC.KD = 1/2. 22.23 = 253(mm²)

S_HKDE = (HE + KD).HK / 2 = (16 + 23).18 / 2= 351 (mm²)

Do đó

S_ABCDE = S_ABC + S_AHE + S_DKC+ S_HKDE = 456 + 64 + 253+ 351

Vậy S_ABCDE = 1124(mm²)

Bài 2:

Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình 153. Hãy tính diện tích phần con đường EBGF (EF//BG) và diện tích phần còn lại của đám đất.

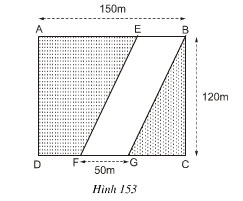
bai-38

Lời giải:

Con đường hình bình hành EBGF có diện tích

S_EBGF = 50.120 = 6000 m²

Đám đất hình chữ nhật ABCD có diện tích

S_ABCD = 150.120 = 18000 m²

Diện tích phần còn lại của đám đất:

S = S_ABCD – S_EBGF = 18000 – 6000 = 12000 m²

Bài 3. Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình 155 (cạnh của mỗi hình vuông là 1cm, tỉ lệ1/10000).

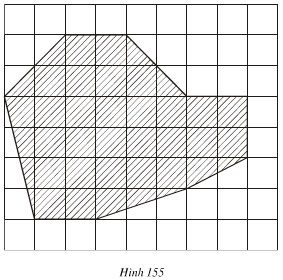
bai-40

Lời giải:

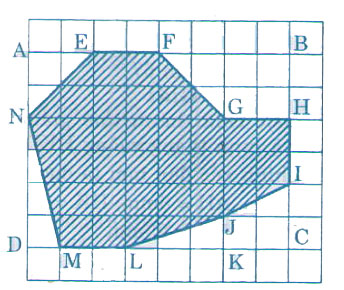
dap-an-bai-40

Diện tích phần gạch sọc trên hình gồm Diện tích hình chữ nhật ABCD trừ đi diện tích các hình tam giác AEN, JKL, DMN và các hình thang BFGH, CIJK. Ta có:

S.hình chữ nhật ABCD là 6 x 8 ô vuông

S.ΔAEN là 2 ô vuông

S.ΔJKL là 1,5 ô vuông

S.ΔDMN là 2 ô vuông

S.hình thang BFGH là 6 ô vuông

S.hình thang CIJK là 3 ô vuông

Do đó tổng diện tích của các hình phải trừ đi là:

2 + 1 + 2 +6 + 3 = 14,5 ô vuông

Nên diệntích phần gạch sọc trên hình là:

6 x 8 – 14,5 = 33,5 ô vuông

Do tỉ lệ xích 1/10000 là nên diện tích thực tế là:

33,5 x 10000 = 335000 cm² = 33,5 m²

Bài 4. Thực hiện phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE có AE // BC (như hình vẽ).

Lời giải:

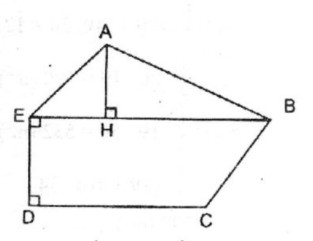
Chia đa giác ABCDE thành ΔABE và hình thang vuông BEDC.

Kẻ AH ⊥ BE .

Dùng thước chia khoảng đo độ dài: BE, DE, CD, AH.

Ta có: S_ABCDE = S_ABE + S_BEDC

Bài 5. Theo bản đồ ghi hình bên tỉ lệ 1:100 , hãy tính điện tích hồ nước phần gạch đậm.

Lời giải:

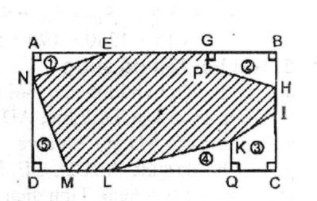
Giả sử hình chữ nhật là ABCD.

Trên AB, 2 giao điểm là E và G.

Trên BC hai giao điểm là I và H.

Trên CD hai giao điểm là L và M. Giao điểm trên AD là N. Hình thang tại đỉnh B có giao điểm là P, điểm trên đường gấp khúc IL là K.

Kẻ KQ ⊥ CD, gọi điện tích phẩn gạch đậm là S.

Ta có: S = S_ABC– S_ANE– S_BHPG– S_ICQK – S_DMN

Dùng thước chia khoảng đo các đoạn (mm):

AB, AD, AE, AN, PG, GB, BH, IC, CQ, QK, LQ, DM

Sau khi thực hiện phép tính, ta lấy kết quả nhân với 100.

Bài 6. Theo kích thước đã cho trên hình. Tính diện tích phân gạch đậm (đơn vị là m²)

Lời giải:

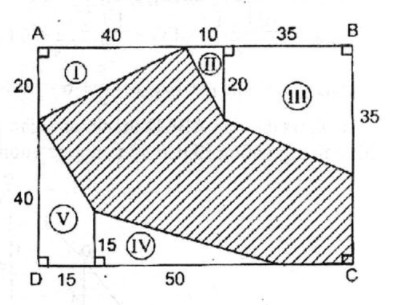
S_ABCD = AD.AB = (20 + 40).(40 + 10 + 35) = 5100 (m²)

S_I= 1/2 .40.20 = 400 (m²)

S_II = 1/2 .10.20 = 100 (m²)

S_III = 1/2 (20 + 35).35 = 962,5 (m²)

S_IV = 1/2 .15.50 = 375 (m²)

S_V = 1/2 (15 + 40).15 = 412,5 (m²)

Diện tích phần gạch đậm:

S = 5100 – (400 + 100 + 962,5 + 375 + 412,5) = 2850 (m²)

Bài 7. Tính diện tích mảnh đất theo kích thước trong hình (đơn vị m²)

Lời giải:

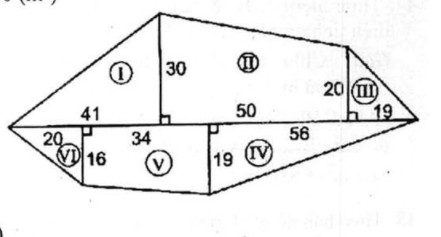
S_I= 1/2 .41.30 = 615 (m²)

S_II = 1/2 (30 + 20).50 = 1250 (m²)

S_III = 1/2 .20.19 = 190 (m²)

S_IV = 1/2 .19.56 = 532 (m²)

S_V = 1/2 (19+16).34 = 595 (m²)

S_VI = 1/2 .16.20 = 160 (m²)

S = S_I + S_II + S_III + S_IV + S_V + S_VI (m²)

= (615 + 1250 + 190 + 532 + 595 + 160) = 3342 (m²).

II. Bài tập vận dụng

Bài 1: Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3cm.

a) Tính diện tích hình bình hành ABCD.

b) Gọi M là trung điểm của AB. Tính diện tích tam giác ADM.

c) DM cắt AC tại N. Chứng minh DN = 2MN.

d) Tính diện tích tam giác AMN.

Bài 2: Cho tam giác ABC có diện tích $30 c m^{2}$ . Các điểm D, E theo thứ tự lấy trên cạnh AC, AB sao cho AD = DC; $A E = \frac{1}{2} E B$ . Gọi K là giao điểm của BD và CE. Tính diện tích tứ giác ADKE.

Bài 3: Tính diện tích tứ giác ABCD biết $\hat{C} = 60 °$ , CA là tia phân giác của góc $\hat{C}$ và CA = 4cm, CB = 3cm, CD = 5cm.

Bài 4: Cho tứ giác ABCD, gọi E là trung điểm của AB, gọi F là trung điểm của CD, gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE. Chứng minh:

a) $S_{E D C} = S_{A D F} + S_{B C F}$

b) $S_{E I F K} = S_{A I D} + S_{B K C}$

Bài 5: Cho tứ giác ABCD. Hãy dựng tam giác ABE $(E \in A D)$ có diện tích bằng diện tích tứ giác ABCD.

Bài 6: Cho tứ giác ABCD có diện tích là S. M là trung điểm của AC. Chứng minh: $S_{A B M D} = \frac{1}{2} S$ .

Bài 7: Cho tam giác ABC cân tại A, có diện tích S. Gọi O là trung điểm của đường cao AH. Gọi D là giao điểm của BO với cạnh AC và E là giao điểm của CO với cạnh AB. Tính diện tích tứ giác ADOE theo S.

Bài 8: Cho tam giác ABC, điểm D thuộc cạnh AC (AD < DC). Hãy kẻ đường thẳng đi qua D và chia tam giác ABC thành hai phần có diện tích bằng nhau.

Bài 9: Cho tứ giác ABCD. Hãy kẻ đường thẳng đi qua A và chia tứ giác ABCD thành hai phần có diện tích bằng nhau.

Bài 10: Cho G là trọng tâm tam giác ABC. Gọi M là giao điểm của BG và AC. Chứng minh:

a) $S_{G B C} = \frac{2}{3} S_{M B C}$

b) $S_{G B C} = S_{G A C} = S_{G A B}$

B. Lý thuyết Diện tích đa giác

1. Lý thuyết

Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương có các tính chất sau:

– Hai tam giác bằng nhau thì có diện tích bằng nhau.

– Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

– Hình vuông cạnh có độ dài bằng 1 thì có diện tích là 1.

2. Các công thức tính diện tích đa giác

– Diện tích hình chữ nhật bằng tích hai kích thước của nó $S = a . b$ (a,b là kích thước hình chữ nhật).

– Diện tích hình vuông bằng bình phương cạnh của nó $S = a^{2}$ (a là độ dài cạnh hình vuông).

– Diện tích hình vuông có đường chéo dài bằng d là $\frac{1}{2} d^{2}$ .

– Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông $S = \frac{1}{2} a . b$ (a,b là độ dài hai cạnh góc vuông).

– Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó $S = \frac{1}{2} a . h$ (a,h là độ dài cạnh và đường cao tương ứng).

– Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao:

$S = \frac{1}{2} (a + b) . h$ (a, b là độ dài hai đáy, h là độ dài đường cao).

– Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó: $S = a . h$ (a, h là độ dài một cạnh và đường cao tương ứng).

– Diện tích tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo.

$S = \frac{1}{2} . d_{1} . d_{2}$ ( $d_{1}$ ; $d_{2}$ là độ dài hai đường chéo tương ứng).

– Diện tích hình thoi bằng nửa tích hai đường chéo $S = \frac{1}{2} . d_{1} . d_{2}$ ( $d_{1}$ ; $d_{2}$ là độ dài hai đường chéo tương ứng).

3. Bổ sung

– Hai tam giác có chung một cạnh (hoặc một cặp cạnh bằng nhau) thì tỉ số diện tích bằng tỉ số hai đường cao ứng với cạnh đó.

– Hai tam giác có chung một đường cao (hoặc một cặp đường cao bằng nhau) thì tỉ số diện tích bằng tỉ số hai cạnh ứng với đường cao đó.

– ABCD là hình thang $(A B // C D)$ . Hai đường chéo AC và BD cắt nhau tại O thì $S_{A O D} = S_{B O C}$ .

– Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

– Hai hình chữ nhật có cùng chiều cao thì tỉ số diện tích bằng tỉ số hai đáy.

– Tam giác đều cạnh a có diện tích là $\frac{a^{2} \sqrt{3}}{4}$ .

Bài liên quan:

Leave a Comment Hủy