Giải SGK Toán 8 Bài 4: Diện tích hình thang

Giải bài tập Toán lớp 8 Bài 4: Diện tích hình thang

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 123 Toán 8 Tập 1:Hãy chia hình thang ABCD thành hai tam giác rồi tính diện tích hình thang theo hai đáy và đường cao (h.136).

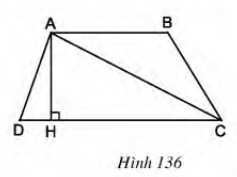
Lời giải

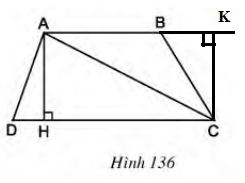
Kẻ CK vuông góc với AB

Tứ giác AHCK có $\widehat{AHC}=\widehat{HAK}=\widehat{AKC}={90}^0$

Suy ra tứ giác AHCK là hình chữ nhật nên AH = CK

S_ADC = $\frac{1}{2}$ AH.DC

S_ABC = $\frac{1}{2}$ CK.AB = $\frac{1}{2}$.AH.AB

S_ABCD = S_ABC + S_ADC 

= $\frac{1}{2}$ AH.AB + $\frac{1}{2}$ AH.DC

= $\frac{1}{2}$ AH.(AB + DC)

Câu hỏi 2 trang 124 Toán 8 Tập 1:Hãy dựa vào công thức tính diện tích hình thang để tính diện tích hình bình hành.

Lời giải

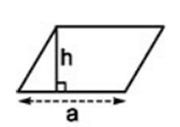
Hình bình hành là hình thang có hai đáy bằng nhau

⇒ Hình bình hành có cạnh đáy a và chiều cao h là:

S = $\frac{1}{2}$h(a + a) =  $\frac{1}{2}$h.2a = a.h.

Bài tập (123; 124)

Bài 26 trang 123 Toán 8 Tập 1:Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828m².

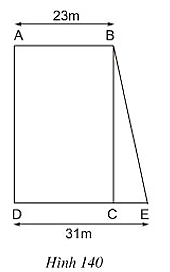
Lời giải

Ta có: Diện tích hình chữ nhật ABCD là: AB.AD = 828m²

Mà AB = 23m ⇒ AD = 828:23 = 36m.

Diện tích hình thang ABED là:

$\begin{array}{l}{S}_{ABED}=\frac{1}{2}\left(AB+ED\right).AD\\ S_{ABED}=\frac{1}{2}\left(23+31\right).36\\ S_{ABED}=972\left(m^2\right)\end{array}$

Vậy diện tích hình thang ABED là 972 m².

Bài 27 trang 123 Toán 8 Tập 1:Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.

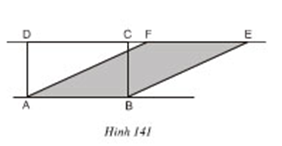
Lời giải:

Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.

Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước:

– Lấy một cạnh của hình bình hành ABEF làm một cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.

– Vẽ đường thẳng EF.

– Từ A và B vẽ các đường thẳng vuông góc với đường thẳng EF chúng cắt đường thẳng EF lần lượt tại D, C. Vẽ các đoạn thẳng AD, BC.

ABCD là hình chữ nhật có cùng diện tích với hình bình hành ABEF đã cho.

Bài 28 trang 124 Toán 8 Tập 1:Xem hình 142 (IG // FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE.

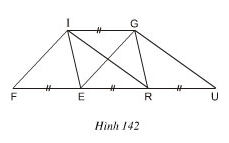
Lời giải:

+ Nhận thấy các hình IGRE và IGUR là hình bình hành.

Gọi h là chiều cao từ I đến cạnh FE, đồng thời là chiều cao từ I đến FU.

⇒ S_IGRE = h.RE

và S_IGUR = h.RU; S_FIGE = h.FE.

Mà FE = RE = RU

⇒ S_FIGE = S_IGRE = S_IGUR.

Ta lại có

S_FIGE = h.FE = $\frac{1}{2}h.2FE=\frac{1}{2}.h.FR$ = S_FIR

Tương tự:

S_FIGE = h.FE = $\frac{1}{2}h.2FE=\frac{1}{2}.h.EU$ = S_GEU

Vậy S_FIGE = S_IGRE = S_IGUR = S_IFR = S_GEU.

Bài 29 trang 124 Toán 8 Tập 1:Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?

Lời giải:

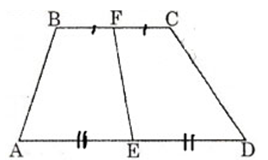
+) Vẽ hình thang ABCD như hình trên. Gọi E, F lần lượt là trung điểm của hai đáy AD BC.

Gọi h là chiều cao của hình thang ABCD. Khi đó h cũng là chiều cao của hình thang BFEA và hình thang FCDE.

+) Diện tích hình thang BFEA là:

$S_{BFEA}=\frac{\left(BF+AE\right)h}{2}$

+) Diện tích hình thang FCDE là:

$S_{FCDE}=\frac{\left(FC+DE\right)h}{2}$

+) Ta lại có: BF = FC (vì F là trung điểm của BC) (3)

AE = DE (vì E là trung điểm của AD) (4)

+) Từ (1); (2); (3) và (4) suy ra: S_BFEA = S_FCDE.

Bài 30 trang 124 Toán 8 Tập 1:Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.

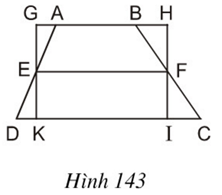
Lời giải

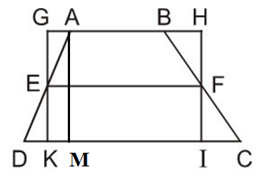
Kẻ đường cao AM của hình thang ABCD

Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.

Xét ΔAEG và ΔDEK, có:

$\widehat{AGE}=\widehat{DKE}={90}^0$

AE = ED (E là trung điểm của AD)

$\widehat{AEG}=\widehat{DEK}$ (hai góc đối đỉnh)

Suy ra: ΔAEG = ΔDEK (cạnh huyền – góc nhọn)

$\Rightarrow S_{\Delta AEG}=S_{\Delta DEK}$

Chứng minh tương tự: ΔBFH = ΔCFI

$\Rightarrow S_{\Delta BFH}=S_{\Delta CFI}$

Do đó S_ABCD = S_AEKIFB + S_DEK + S_CFI 

= S_AEKIFB + S_AEG + S_BFH = S_GHIK

Nên S_ABCD = S_GHIK

Mà S_GHIK = GH.GK= EF. AM ( vì GH = EF, GK = AM)

Nên S_ABCD = EF. AM

Ta lại có: $FE=\frac{AB+CD}{2}$

$\Rightarrow S_{ABCD}=\frac{AB+CD}{2}.AM$.

Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp chứng minh khác.

Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.

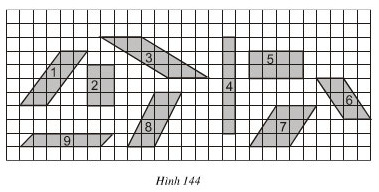
Bài 31 trang 124 Toán 8 Tập 1:Xem hình 144. Hãy chỉ ra các hình có cùng diện tích (lấy ô vuông làm đơn vị diện tích).

Lời giải:

Các hình 2, 6, 9 có cùng diện tích là 6 ô vuông.

Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.

Các hình 3, 7 có cùng diện tích là 9 ô vuông.

Hình 4 có diện tích là 7 ô vuông nên không có cùng diện tích với một trong các hình đã cho.