50 Bài tập Hình vuông (có đáp án)- Toán 8

Bài tập Toán 8 Chương 1 Bài 12: Hình vuông

A. Bài tập Hình vuông

I. Bài tập trắc nghiệm

Bài 1: Hãy khoanh tròn vào phương án đúng nhất trong các phương án sau ?

A. Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.

B. Hình vuông là tứ giác có 4 góc bằng nhau.

C. Hình vuông là tứ giác có 4 cạnh bằng nhau.

D. Hình vuông là tứ giác có hai cạnh kề bằng nhau.

Lời giải:

+ Tứ giác có 4 góc vuông là hình chữ nhật

Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.

⇒ Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.

Chọn đáp án A.

Bài 2: Hãy chọn đáp án sai trong các phương án sau đây ?

A. Trong hình vuông có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

B. Trong hình vuông có hai đường chéo không vuông góc với nhau.

C. Trong hình vuông thì hai đường chéo đồng thời là hai trục đối xứng của hình vuông.

D. Trong hình vuông có hai đường chéo vuông góc với nhau và bằng nhau.

Lời giải:

+ Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường

+ Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.

→ Đáp án B sai.

Chọn đáp án B.

Bài 3: Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?

A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

B. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

C. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

D. Hình bình hành có hai đường chéo bằng nhau là hình vuông.

Lời giải:

Dấu hiệu nhận biết hình vuông:

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

→ Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.

→ Đáp án D sai.

Chọn đáp án D.

Bài 4: Tìm câu nói đúng khi nói về hình vuông?

A. Hình vuông vừa là hình chữ nhật, vừa là hình thoi.

B. Hình thoi có một góc vuông là hình vuông.

C. Hình thoi có hai đường chéo bằng nhau là hình vuông.

D. Các phương án đều đúng.

Lời giải:

Dấu hiệu nhận biết hình vuông:

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

⇒ Hình vuông vừa là hình chữ nhật, cũng vừa là hình thoi.

⇒ Cả 3 phương án đều đúng.

Chọn đáp án D.

Bài 5: Một hình vuông có độ dài cạnh bằng 4cm thì độ dài đường chéo của hình vuông là ?

A. 8cm   

B. $\sqrt{32}$ cm

C. 5cm   

D. 4cm

Lời giải:

Hình vuông có độ dài cạnh là a ( cm )

Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là $a\sqrt{2}$ ( cm )

Do đó với a = 4 thì độ dài đường chéo là $4\sqrt{2}$ = $\sqrt{32}$ ( cm )

Chọn đáp án B.

Bài 6: Hình bình hành có 1 góc vuông là:

A. Hình thoi

B. Hình chữ nhật

C. Hình vuông

D. Hình thang cân.

Lời giải:

Hình bình hành có 1 góc vuông là hình chữ nhật

Chọn đáp án B

Bài 7: Cho hình vuông ABCD có AC = $10\sqrt{2}$cm . Tính diện tích hình vuông?

A. 200 cm²    

B. 100 cm²

C. 400 cm²    

D. 50cm²

Lời giải:

Gọi độ dài cạnh hình vuông là a.

Suy ra: AB = BC = CD = D = a

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:

Do đó, diện tích hình vuông đã cho là: S = a² = 100 cm²

Chọn đáp án B

Bài 8: Cho hình vuông ABCD có O là giao điểm hai đường chéo. Hình vuông có diện tích 400cm². Tính OA?

A. 10cm    

B. 20cm

C. $10\sqrt{2}$ cm    

D. $20\sqrt{2}$cm

Lời giải:

Diện tích hình vuông là: S = AB² = 400 nên AB = 20 cm

Áp dụng định lí Pyta go vào tam giác vuông ABC ta có:

AC² = AB² + BC² = 20² + 20² = 800

Suy ra: AC = $20\sqrt{2}$cm

Vì ABCD là hình vuông có O là giao điểm của hai đường chéo nên O là trung điểm của AC

Suy ra:

Chọn đáp án C

Bài 9: Cho tam giác ABC vuông cân tại A có M; N và H lần lượt là trung điểm của AB; AC và BC. Hỏi tứ giác AMHN là hình gì ? Chọn câu trả lời đúng nhất

A. Hình vuông

B. Hình chữ nhật

C. Hình thoi

D. Hình thang vuông

Lời giải:

* Vì N và H lần lượt là trung điểm của AC và BC nên NH là đường trung bình của tam giác

Suy ra: NH// AB và

* Chứng minh tương tự, có MH là đường trung bình của tam giác ABC nên:

MH// AN và

* Tứ giác AMHN có 2 các cạnh đối song song với nhau nên là hình bình hành

Lại có : $\widehat{BAC}$ = 90^o nên tứ giác AMHN là hình chữ nhât.

* Theo giả thiết, tam giác ABC là tam giác vuông cân tại A nên AC = AB (3)

Từ (1); (2) và (3) suy ra: NH = MH.

Hình chữ nhật AMHN có hai cạnh liền kề NH và MH bằng nhau nên là hình vuông

Chọn đáp án A

Bài 10: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q theo thứ tự là trung điểm của AB; BC; CD và DA. Hỏi tứ giác MNPQ là hình gì

A. Hình bình hành

B. Hình thoi

C. Hình chữ nhật

D. Hình vuông

Lời giải:

* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác .

Suy ra: MN// AC và

* Xét tam giác ACD có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác

Suy ra: PQ // AC và

Từ (1) và (2) suy ra: MN// PQ và MN = PQ

Do đó, tứ giác MNPQ là hình bình hành.

* Ta có

Hình bình hành MNPQ có 1 góc vuông nên là hình chữ nhật

Chọn đáp án C

Bài 11: Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:

A. 4cm

B. 7 cm           

C. 14 cm         

D. 8 cm

Lời giải:

Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông bằng 4a. (a là độ dài một cạnh)

Từ giả thiết ta có 4a = 28 ⇔ a = 7cm.

Vậy cạnh hình vuông là a = 7cm

Đáp án cần chọn là: B

Bài 12: Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:

A. 10cm         

B. 15 cm         

C. 5 cm           

D. 8 cm

Lời giải:

Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông bằng 4a. (a là độ dài một cạnh)

Từ giả thiết ta có 4a = 32 ⇔ a = 8cm.

Vậy cạnh hình vuông là a = 8cm

Đáp án cần chọn là: D

Bài 13: Cho hình vuông có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông là:

A. 32              

B. 16              

C. 24              

D. 18

Lời giải:

Gọi hình vuông ABCD có chu vi là 16cm. Khi đó 4.AB = 16cm

⇒ AB = 4cm = AB = CD = DA

Xét tam giác ABC vuông tại B, theo định lý Pytago ta có

AB² + BC² = AC² ⇒ AC² = 4² + 4² ⇔ AC² = 32

Vậy bình phương độ dài một đường chéo là: 32

Đáp án cần chọn là: A

Bài 14: Cho hình vuông có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông là:

A. 32              

B. 50              

C. 25              

D. 30

Lời giải:

Gọi hình vuông ABCD có chu vi là 20cm. Khi đó 4.AB = 20cm

⇒ AB = 5cm = AB = CD = DA

Xét tam giác ABC vuông tại B, theo định lý Pytago ta có

AB² + BC² = AC² ⇒ AC² = 5² + 5² ⇔ AC² = 50

Vậy bình phương độ dài một đường chéo là: 50

Đáp án cần chọn là: B

Bài 15: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.

A. BD ⊥ AC; BD = AC                     

B. BD ⊥ AC

C. BD = AC                                       

D. AC = BD và AB // CD

Lời giải:

Ta có EH; EF lần lượt là đường trung bình của tam giác ABD; BAC nên  (1)

Hình bình hành EFGH là hình vuông khi và chỉ khi  (2)

Từ (1); (2) ⇒  thì hình bình hành EFGH là hình vuông

Đáp án cần chọn là: A

II. Bài tập tự luận có giải

Bài 1: Đường chéo của hình vuông có những tính chất gì ?

Lời giải

Hình vuông có tất cả các hình chữ nhật và hình thoi

⇒ Hai đường chéo của hình vuông có tính chất:

Hai đường chéo bằng nhau

Hai đường chéo cắt nhau tại trung điểm mỗi đường

Hai đường chéo vuông góc với nhau

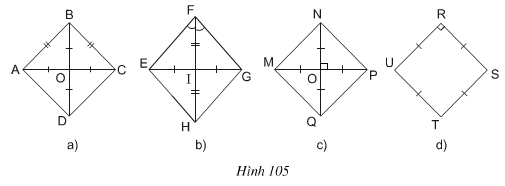
Bài  2 Tìm các hình vuông trên hình 105.

Lời giải

– ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABCD là hình bình hành

Hình bình hành ABCD có hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật

Hình chữ nhật ABCD có AB = BC ⇒ ABCD là hình vuông

– MNPQ có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ MNPQ là hình bình hành

Hình bình hành MNPQ có hai đường chéo bằng nhau ⇒ MNPQ là hình chữ nhật

Hình chữ nhật MNPQ có MP ⊥ NQ tại O ⇒ MNPQ là hình vuông

– RSTU có 4 cạnh bằng nhau ⇒ RSTU là hình thoi

Hình thoi RSTU có một góc vuông ⇒ RSTU là hình vuông

Bài 3 a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, $\sqrt{18}$ cm, 5cm hay 4cm?

b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng:

Lời giải:

a)

Gọi đường chéo của hình vuông có độ dài là a.

Áp dụng định lí Pi-ta-go ta có:

a² = 3² + 3² = 18 suy ra a = $\sqrt{18}=3\sqrt{2}$

Vậy đường chéo của hình vuông đó bằng $3\sqrt{2}$ (cm)

b)

Gọi cạnh của hình vuông là a.

Áp dụng định lí Pi-ta-go ta có:

a² + a² = 2² ⇒ 2a² = 4

⇒ a² = 2 ⇒ a = $\sqrt{2}$

Vậy cạnh của hình vuông đó bằng $\sqrt{2}$ (dm).

Bài 4 Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Lời giải:

+ Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.

+ Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.

+ Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.

Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.

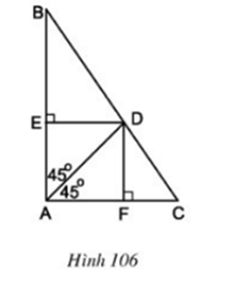
Bài 5 Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

Lời giải:

Cách 1:

Tứ giác AEDF có EA // DF (cùng vuông góc AF)

DE // FA (cùng vuông góc AE)

⇒ AEDF là hình bình hành (theo định nghĩa)

Hình bình hành AEDF có đường chéo AD là phân giác của góc A

⇒AEDF là hình thoi.

Hình thoi AEDF có Â = 90º

⇒ AEDF là hình vuông.

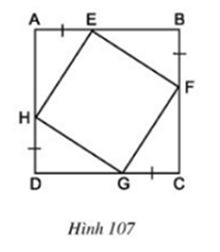
Bài 6 Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Lời giải:

* Do ABCD là hình vuông nên AB = BC = CD = DA.

Theo giả thiết ta có: AE = BF = CG = DH nên ta có:

AB – AE = BC – BF = CD – CG = DA – DH

⇔ BE = CF= DG = HA

* Xét các tam giác vuông AEH, BFE, CGF, DHG có:

AE= BF = CG = DH (giả thiết)

HA= BE = CF = DG (chứng minh trên)

⇒ ΔAEH = ΔBFE = ΔCGF = ΔDHG ( c.g.c)

Suy ra: HE = EF = FG = GH (các cạnh tương ứng)

* Tứ giác EFGH là hình thoi có 1 góc bằng 90^o nên EFGH là hình vuông.

Bài 7 Các câu sau đúng hay sai?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Lời giải:

– Các câu a và d sai.

– Các câu b, c, e đúng.

Bài 8 Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Lời giải:

a) Tứ giác AEDF là hình bình hành.

Vì có DE // AF, DF // AE (gt) (theo định nghĩa)

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).

d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Bài 9 Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Lời giải:

a) E, F là trung điểm AB, CD ⇒ AE = EB = $\frac{AB}{2}$, DF = FC = $\frac{CD}{2}$.

Ta có: AB = CD = 2AD = 2BC

⇒ AE = EB = BC = CF = FD = DA.

+ Tứ giác ADFE có AE // DF, AE = DF

⇒ ADFE là hình bình hành.

Hình bình hành ADFE có Â = 90º

⇒ ADFE là hình chữ nhật.

Hình chữ nhật ADFE là hình chữ nhật có AE= AD

⇒ ADFE là hình vuông.

b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành

Do đó DE // BF

Tương tự: AF // EC

Suy ra EMFN là hình bình hành

Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.

Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.

Lại có ME = MF nên EMFN là hình vuông.

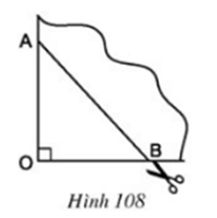
Bài 10 Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?

Lời giải:

– Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.

– Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

III. Bài tập vận dụng

Bài 1 Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của  BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác MENF là hình gì? Vì sao?

Bài 2 Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ. Chứng minh rằng tứ giác MNPQ là hình vuông.

Bài 3 Cho $\mathrm{\Delta }$ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB, AC lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?

Bài 4 Cho một hình chữ nhật có hai cạnh kể không bằng nhau. Chứng minh rằng các tia phân giác của các góc của hình chữ nhật đó cắt nhau tạo thành một hình vuông.

Bài 5 Cho hình vuông ABCD. Trên tia AD lấy điểm E, trên tia đối của tia AD lấy điểm F, trên tia đối của tia BA lấy điểm I sao cho DE = AF = BI. Vẽ hình vuông AFGH, H thuộc cạnh AB. Chứng minh rằng tứ giác EGIC là hình vuông.

Bài 6 Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm,    $\sqrt{18}$cm, 5cm hay 4cm?

b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng:

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Bài 7 Các câu sau đúng hay sai?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Bài 8 Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Bài 9 Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Bài 10 Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?

Bài 11 Đường chéo của hình vuông có những tính chất gì ?

Bài 12 Tìm các hình vuông trên hình 105

Bài 13 Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN. Chứng minh rằng AM = BN và AM  BN.

Bài 14 Cho ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

Bài 15 Cho hình vuông ABCD cạnh a. Gọi E là một điểm nằm giữa C và D. Tia phân giác của $\widehat{DAE}$ cắt CD ở F. Kẻ FH $\perp$ AE (H $\in$ AE). FH cắt BC ở K.

a) Tính độ dài AH.

b) Tính số đo $\widehat{FAK}$

Bài 16 Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của BC, CD và I là giao điểm của AN, DM. Chứng minh rằng:

a) AN $\perp$ DM

b) AB = BI

Bài 17 Cho một hình vuông cạnh dài 1m. Vẽ hình vuông thứ hai nhận đường chéo của hình vuông đã cho làm cạnh. Tính độ dài đường chéo của hình vuông này.

B. Lý thuyết Hình vuông

1. Định nghĩa

Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Tổng quát: ABCD là hình vuông ⇔

Nhận xét:

+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

+ Hình vuông là hình thoi có bốn góc vuông.

+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.

2. Tính chất

Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

3. Dấu hiệu nhận biết hình vuông

Note keypoint

Skip

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

Hướng dẫn:

+ Xét tứ giác AEDF có Aˆ = Eˆ = Fˆ = 90⁰

⇒ AEDF là hình chữ nhật .       ( 1 )

Theo giả thiết ta có AD là đường phân giác của góc Aˆ

⇒ EADˆ = DAFˆ = 45⁰.

+ Xét Δ AED có AEDˆ = 90⁰; DAEˆ = 45⁰ ⇒ EDAˆ = 45⁰

⇒ Δ AED vuông cân tại E nên AE = ED       ( 2 )

Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)