50 Bài tập Quy đồng mẫu thức nhiều phân thức (có đáp án)- Toán 8

Bài tập Toán 8 Chương 2 Bài 4: Quy đồng mẫu thức nhiều phân thức

A. Bài tập Quy đồng mẫu thức nhiều phân thức

I. Bài tập trắc nghiệm

Bài 1: Hai phân thức $\frac{1}{\left(4x^{2}y\right)}$ và $\frac{5}{\left(6x{y}^3\right)}$ có mẫu thức chung đơn giản nhất là?

A. 8x²y³z

B. 12x³y³z

C. 24x²y³z

D. 12x²y³z

Lời giải:

Ta có ⇒ Mẫu thức chung đơn giản nhất là: 12x²y³z

Chọn đáp án D.

Bài 2: Hai phân thức $\frac{5}{\left(2x+6\right)}$ và $\frac{3}{\left(x^2–9\right)}$ có mẫu thức chung đơn giản nhất là ?

A. x² – 9.

B. 2(x² – 9 ).

C. x² + 9.

D. x – 3

Lời giải:

Ta có: ⇒ MTC = 2( x – 3 )( x + 3 )

= 2( x² – 9 )

Chọn đáp án B.

Bài 3: Hai phân thức $\frac{(x + 1)}{(x^2 + 2x – 3)}$ và $\frac{(– 2x)}{(x^2 + 7x + 10)}$ có mẫu thức chung là ?

A. x³ + 6x² + 3x – 10

B. x³ – 6x² + 3x – 10

C. x³ + 6x² – 3x – 10

D. Đáp án khác

Lời giải:

Chọn đáp án D.

Bài 4: Tìm mẫu thức chung của hai phân thức sau:

A. xy²(x + y)    

B. xy²

C. xy²(x + 1)    

D. xy(x + y + 1)

Lời giải:

Ta có: x² + xy = x.(x + y)

Suy ra, mẫu thức chung của 2 phân thức đã cho là: x.y².(x + y)

Chọn đáp án A

Bài 5: Quy đồng mẫu thức hai phân thức:

Lời giải:

Ta có: 2x – 2xy = 2x.(1 – y)

Do đó, mẫu thức chung của hai phân thức đã cho là: 2x.(1 – y)

Suy ra, nhân tử phụ của phân thức thứ nhất là x. (1- y) nên:

Nhân tử phụ của phân thức thứ hai là 1 nên:

Chọn đáp án A

Bài 6: Tìm mẫu thức chung của hai phân thức:

A. xy(x + y)    

B. x(x + y)²

C. xy(x + y)²    

D. y(x + y)²

Lời giải:

Ta có: x²y + xy² = xy.(x + y)

Và x² + 2xy + y² = (x + y)²

Suy ra: Mẫu thức chung của hai phân thức đã cho là: xy.(x + y)²

Chọn đáp án C

Bài 7: Cho hai phân thức:

Tìm nhân tử phụ của mẫu thức x² – 4x²y + 4xy² – y²

A. x(x – y).(x + y – 4xy)    

B. x

C. x – y    

D. Đáp án khác

Lời giải:

Ta có: x² – 4x²y + 4xy² – y² = (x² – y²) – (4x²y – 4xy²)

= (x + y).(x – y) – 4xy. (x – y) = (x – y).(x + y – 4xy)

Và x² – xy = x. (x – y)

Do đó, mẫu thức chung là: x(x – y).(x + y – 4xy)

Vậy nhân tử phụ của mẫu thức x² – 4x²y + 4xy² – y² là x.

Chọn đáp án B

Bài 8: Quy đồng mẫu thức của hai phân thức sau ta được:

Lời giải:

Ta có: x²y + 4xy + 4y = y(x² + 4x + 4) = y.(x + 2)²

Và x² + 2x = x.(x + 2)

Do đó mẫu thức chung của 2 phân thức đã cho là: xy(x + 2)²

Ta có: nhân tử phụ của mẫu thức x²y + 4xy + 4y là x; nhân tử phụ của x² + 2x là y(x + 2):

Chọn đáp án D

Bài 9: Quy đồng mẫu thức hai phân thức:

Lời giải:

Ta có: x²y + x² = x²(y + 1) và y + 1 = y + 1

Do đó, mẫu thức chung của hai phân thức là: x².(y + 1).

Nhân tử phụ của mẫu thức x²(y + 1) là 1 và nhân tử phụ của mẫu thức y + 1 là x²

Suy ra:

Chọn đáp án C

Bài 10: Cho hai phân thức sau. Tìm nhân tử phụ của mẫu thức x³ + 2x²y

Lời giải:

Ta có: x² + 2xy = x.(x + 2y) và (x³ + 2x²y) = x²(x + 2y)

Do đó mẫu thức chung là x² (x + 2y)

Suy ra, nhân tử phụ của mẫu thức x³ + 2x²y là 1

Chọn đáp án A

II. Bài tập tự luận

Bài 1: Quy đồng mẫu thức của các phân thức 

Lời giải

Ta có x² – 1 = (x – 1)(x + 1) và BCNN(2;3) = 6 nên các phân thức  có mẫu chung là 6(x – 1)(x + 1) = 6(x² – 1).

* Nên nhân tử phụ của  là 2(x + 1) ⇒

* Nhân tử phụ của  là 3(x – 1) ⇒ .

* Nhân tử phụ của  là 6 ⇒

Bài 2: Quy đồng mẫu thức các phân thức  ta được các phân thức lần lượt là?

Lời giải

Ta có: x³ + 1 = (x + 1)(x² – x + 1); 3x + 3 = 3(x + 1); 2x² – 2x + 2 = 2(x² – x + 1) và BCNN(2;3) = 6 nên các phân thức  có mẫu chung là 6(x + 1)(x² – x + 1) = 6(x³ + 1).

* Nên nhân tử phụ 

* Nhân tử phụ của  là 2(x² – x + 1)

* Nhân tử phụ của  là 3(x + 1)

Bài 3: Cho . Điền vào chỗ trống để được các phân thức có cùng mẫu.

Lời giải

Ta có mẫu thức chung của hai phân thức là 2x(x + 2) = 2x² + 4x

Do đó nhân cả tử và mẫu của phân thức  với 2x ta được:

Nhân cả tử và mẫu của phân thức  với (x + 2) ta được:

Vậy các đa thức cần điền lần lượt là 4x; x + 2.

Bài 4. Qui đồng mẫu thức các phân thức sau:

$\begin{array}{l}a.\frac{5}{2x+6},\frac{3}{x^2-9}\\ b.\frac{2x}{x^2-8x+16},\frac{x}{3x^2-12x}\end{array}$

Lời giải:

– Tìm mẫu thức chung.

– Áp dụng qui tắc qui đồng mẫu thức.

a) Tìm MTC:

2x + 6 = 2(x + 3)

x² – 9 = (x – 3)(x + 3)

MTC = 2(x – 3)(x + 3) = 2(x² – 9)

Nhân tử phụ:

2(x – 3)(x + 3) : 2(x + 3) = x – 3

2(x – 3)(x + 3) : (x² – 9) = 2

Qui đồng:

$\begin{array}{l}\frac{5}{2x+6}=\frac{5}{2(x+3)}=\frac{5(x-3)}{2(x-3)(x+3)}\\ \frac{3}{x^2-9}=\frac{3}{(x-3)(x+3)}=\frac{3.2}{2(x-3)(x+3)}=\frac{6}{2(x-3)(x+3)}\end{array}$

b) Tìm MTC:

x² – 8x + 16 = (x – 4)²

3x² – 12x = 3x(x – 4)

MTC = 3x(x – 4)²

Nhân tử phụ:

3x(x – 4)² : (x – 4)² = 3x

3x(x – 4)² : 3x(x – 4) = x – 4

Qui đồng:

$\begin{array}{l}\frac{2x}{x^2-8x+16}=\frac{2x}{{(x-4)}^2}=\frac{2x.3x}{3x{(x-4)}^2}=\frac{6x^2}{3x{(x-4)}^2}\\ \frac{x}{3x^2-12}=\frac{x}{3x(x-4)}=\frac{x(x-4)}{3x{(x-4)}^2}\end{array}$

Bài 5. Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):

$\begin{array}{l}a.\frac{4x^2-3x+5}{x^3-1},\frac{1-2x}{x^2+x+1},-2\\ b.\frac{10}{x+2},\frac{5}{2x-4},\frac{1}{6-3x}\end{array}$

Lời giải:

a) Tìm MTC: x³– 1 = (x – 1)(x²+ x + 1)

Nên MTC = (x – 1)(x² + x + 1)

Nhân tử phụ:

(x³ – 1) : (x³ – 1) = 1

(x – 1)(x² + x + 1) : (x² + x + 1) = x – 1

(x – 1)(x² + x + 1) : 1 = (x – 1)(x² + x + 1)

Qui đồng:

$\begin{array}{l}\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{(x-1)(x^2+x+1)}\\ \frac{1-2x}{x^2+x+1}=\frac{(x-1)(1-2x)}{(x-1)(x^2+x+1)}\\ -2=\frac{-2(x^3-1)}{(x-1)(x^2+x+1)}\end{array}$

b) Tìm MTC: x + 2

2x – 4 = 2(x – 2)

6 – 3x = 3(2 – x)

MTC = 6(x – 2)(x + 2)

Nhân tử phụ:

6(x – 2)(x + 2) : (x + 2) = 6(x – 2)

6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)

6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)

Qui đồng:

$\begin{array}{l}\frac{10}{x+2}=\frac{\mathrm{10.6.}(x-2)}{6(x-2)(x+2)}=\frac{60(x-2)}{6(x-2)(x+2)}\\ \frac{5}{2x-4}=\frac{5}{x(x-2)}=\frac{5.3(x+2)}{2(x-2).3(x+2)}\\ \frac{1}{6-3x}=\frac{1}{-3(x-2)}=\frac{-2(x+2)}{-3(x-2).(-2(x+2))}\end{array}$

Bài 6: Cho hai phân thức: $\frac{5x^2}{x^3-6x^2},\frac{3x^2+18x}{x^2-36}$

Khi qui đồng mẫu thức, bạn Tuấn đã chọn MTC = x²(x – 6)(x + 6), còn bạn Lan bảo rằng: “Quá đơn giản! MTC = x – 6”. Đố em biết bạn nào đúng?

Lời giải:

– Cách làm của bạn Tuấn:

x³ – 6x² = x²(x – 6)

x² – 36 = x² – 6² = (x – 6)(x + 6)

MTC = x²(x – 6)(x + 6) => Nên bạn Tuấn làm đúng.

– Cách làm của bạn Lan:

$\begin{array}{l}\frac{5{\mathrm{x}}^2}{x^3-6{\mathrm{x}}^2}=\frac{5{\mathrm{x}}^2}{x^2\left(x-6\right)}=\frac{5}{x-6}\\ \frac{3{\mathrm{x}}^2+18\mathrm{x}}{x^2-36}=\frac{3\mathrm{x}\left(x+6\right)}{\left(x-6\right)\left(x+6\right)}=\frac{3\mathrm{x}}{x-6}\end{array}$

MTC = x – 6 => Nên bạn Lan làm đúng.

Vậy cả hai bạn đều làm đúng. Bạn Tuấn đã tìm MTC theo đúng qui tắc. Bạn Lan thì rút gọn các phân thức trước khi tìm MTC.

Bài 7. Quy đồng mẫu thức hai phân thức:

$\begin{array}{l}a.\frac{3x}{2x+4}\mathrm{\&}\frac{x+3}{x^2-4}\\ b.\frac{x+5}{x^2+4x+4}\mathrm{\&}\frac{x}{3x+6}\end{array}$

Lời giải:

a) Ta có:

2x + 4 = 2(x + 2)

x² – 4 = (x + 2)(x – 2)

MTC : 2(x+2)(x-2)

Nhân tử phụ của MT 2x + 4 là: x – 2

Nhân tử phụ của MT x2 – 4 là: 2

$\begin{array}{l}\frac{3x}{2x+4}=\frac{3x\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}=\frac{3x\left(x-2\right)}{2\left(x^2-4\right)}\\ \frac{x+3}{x^2-4}=\frac{\left(x+3\right).2}{\left(x-2\right)\left(x+2\right).2}=\frac{2\left(x+3\right)}{2\left(x^2-4\right)}\end{array}$

b) Ta có:

x² + 4x + 4 = (x + 2)²

3x + 6 = 3(x + 2)

MTC : 3(x+2)²

Nhân tử phụ của MT x² + 4x + 4 là: 3

Nhân tử phụ của MT 3x + 6 là: x + 2

$\begin{array}{l}\frac{x+5}{x^2+4x+4}=\frac{\left(x+5\right).3}{{\left(x+2\right)}^2.3}=\frac{3\left(x+5\right)}{3{\left(x+2\right)}^2}\\ \frac{x}{3x+6}=\frac{x.\left(x+2\right)}{3\left(x+2\right).\left(x+2\right)}=\frac{x\left(x+2\right)}{3{\left(x+2\right)}^2}\end{array}$

Bài 8. Quy đồng mẫu thức các phân thức sau:

$\begin{array}{l}a.\frac{1}{x+2},\frac{8}{2x-x^2}\\ b.x^2+1,\frac{x^4}{x^2-1}\\ c.\frac{x^3}{x^3-3x^{2}y+3x{y}^2-y^3},\frac{x}{y^2-xy}\end{array}$

Giải:

a) Ta có:

x² – 2x = x(x – 2)

MTC:  x(x + 2)(x – 2)

Nhân tử phụ của MT x + 2 là: 2(x – 2)

Nhân tử phụ của MT x² – 2x là: x + 2

QĐ:

$\begin{array}{l}\frac{1}{x+2}=\frac{1}{2+x}=\frac{x\left(2-x\right)}{x\left(2-x\right)\left(2+x\right)}=\frac{2x-x^2}{x(2-x)(2+x)}\\ \frac{8}{2x-x^2}=\frac{8.(2+x)}{x(2-x)(2+x)}=\frac{16+8x}{x(2-x)(2+x)}\end{array}$

b) Ta có:

x² + 1 có mẫu là 1

MTC: x² – 1

Nhân tử phụ của MT 1 là: x² – 1

Nhân tử phụ của MT x² – 1 là: 1

QĐ:

$\begin{array}{l}{x}^2+1=\frac{x^2+1}{1}=\frac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\frac{x^4-1}{x^2-1}\\ \frac{x^4}{x^2-1}\end{array}$

c) Ta có:

x³ – 3x²y + 3xy² – y³ = (x – y)³

y² – xy = y (y – x)= – y (x – y)

MTC: y (x – y)³

QĐ:

$\begin{array}{l}\frac{x^3}{x^3-3x^{2}y+3x{y}^2}=\frac{x^3}{{\left(x-y\right)}^3}=\frac{x^{3}y}{y{\left(x-y\right)}^3}\\ \frac{x}{y^2-xy}=\frac{x}{y\left(y-x\right)}=\frac{x}{-y\left(x-y\right)}=\frac{-x}{y\left(x-y\right)}\end{array}$

Bài 9. Qui đồng mẫu thức các phân thức sau:

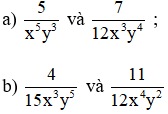
Lời giải

a) Chọn mẫu thức chung đơn giản nhất là 12x⁵y⁴

Nhân tử phụ:

12x⁵y⁴ : x⁵y³ = 12y

12x⁵y⁴ : 12x³y⁴ = x²

Qui đồng:

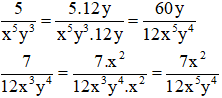
b) Chọn mẫu thức chung đơn giản nhất là 60x⁴y⁵

Nhân tử phụ:

60x⁴y⁵ : 15x³y⁵ = 4x

60x⁴y⁵ : 12x⁴y² = 5y³

Qui đồng:

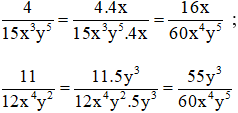
Bài 10: Qui đồng mẫu thức các phân thức sau:

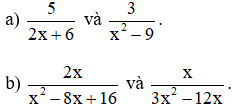
Lời giải:

a) + Phân tích các mẫu thức thành nhân tử để tìm mẫu thức chung

   2x + 6 = 2.(x + 3)

   x² – 9 = (x – 3)(x + 3)

⇒ Mẫu thức chung là 2(x + 3)(x – 3)

Nhân tử phụ thứ nhất: x- 3

Nhân tử phụ thứ hai: 2

+ Quy đồng :

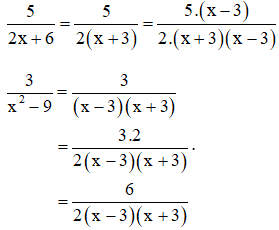
b) * Phân tích các mẫu thức thành nhân tử:

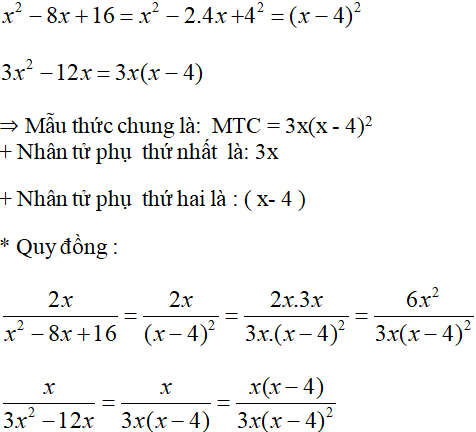
III. Bài tập vận dụng

Bài 1: Quy đồng mẫu thức các phân thức sau:

a) $\frac{5}{x^5{y}^3}$; $\frac{7}{12x^3{y}^4}$

b) $\frac{4}{15x^3{y}^5}$; $\frac{11}{12x^4{y}^2}$

Bài 2: Quy đồng mẫu thức các phân thức:

a) $\frac{3x}{2x+4}$ và $\frac{x+3}{x^2-4}$

b) $\frac{x+5}{x^2+4x+4}$ và $\frac{x}{3x+6}$

Bài 3: Quy đồng mẫu thức các phân thức sau:

a) $\frac{x+2}{x-1}$ và $\frac{x+3}{x+1}$

b) $\frac{2}{x-1}$ và $\frac{x+2}{x^2-1}$

Bài 4: Quy đồng mẫu thức các phân thức sau:

c) $\frac{3}{x-2}$ và $\frac{5}{2x-x^2}$

d) $\frac{x+1}{x-1}$ và $\frac{2x+5}{x^3-1}$

Bài 5:

a) Xác định a, b, c để $\frac{9x^2-16x+4}{x^3-3x^2+2x}=\frac{a}{x}+\frac{b}{x-1}+\frac{c}{x-2}$

b) Áp dụng viết phân thức $\frac{10x-4}{x^3-4x}$ dưới dạng tổng của ba phân thức có tử số là hằng số, mẫu theo thứ tự bằng x, x-2 và x+2

Bài 6

Quy đồng mẫu thức các phân thức sau:

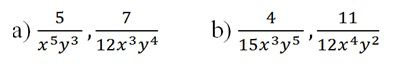
Bài 7 Quy đồng mẫu thức các phân thức sau:

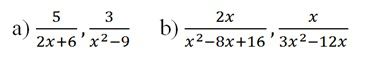
Bài 8: Quy đồng mẫu thức các phân thức sau:

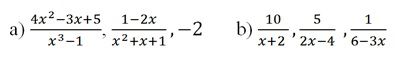
Bài 9: Cho hai phân thức

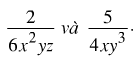
Có thể chọn mẫu thức chung là 12x² y³z hoặc 24x³ y⁴z hay không? Nếu được thì mẫu thức chung nào đơn giản hơn?

Bài 10: Quy đồng mẫu thức hai phân thức:

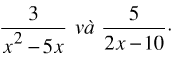
B. Lý thuyết Quy đồng mẫu thức nhiều phân thức

1. Khái niệm

Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.

Ta thường kí hiệu “mẫu thức chung” bởi MTC.

2. Tìm mẫu thức chung

Khi quy đồng mẫu thức nhiều phân thức, muốn tìm mẫu thức chung ta có thể làm như sau:

• Phân tích mẫu thức của các phân thức đã cho thành nhân tử;

• Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:

 +  Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số ở các mẫu thức của các phân thức đã cho. (Nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử bằng số của mẫu thức chung là BCNN của chúng).

 + Với mỗi luỹ thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn luỹ thừa với số mũ cao nhất.

Ví dụ 1. Tìm mẫu thức chung của hai phân thức $\frac{2}{3x^2-6x+3}$ và $\frac{3}{7x^2-7x}$.

Hướng dẫn giải:

+ Phân tích các mẫu thức thành nhân tử:

3x² – 6x + 3 = 3(x² – 2x + 1) = 3(x – 1)²

7x² – 7x = 7x(x – 1)

+ Chọn mẫu thức chung:

Mẫu thức chung của số nguyên là BCNN(3, 7) = 21.

Mẫu thức chung của lũy thừa x là x.

Mẫu thức chung của lũy thừa (x – 1) là (x – 1)².

Do đó: MTC = 21x(x – 1)².

Vậy mẫu thức chung của hai phân thức đã cho là 21x(x – 1)².

3. Quy đồng mẫu thức

Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

– Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;

– Tìm nhân tử phụ của mỗi mẫu thức;

– Nhân tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Ví dụ 2. Quy đồng mẫu thức hai phân thức: $\frac{2}{3x^2-6x+3}$ và $\frac{3}{7x^2-7x}$.

Hướng dẫn giải:

Ở ví dụ 1 trên ta đã tìm được mẫu thức chung của hai phân thức $\frac{2}{3x^2-6x+3}$ và $\frac{3}{7x^2-7x}$ là 21x(x – 1)².

+ Vì 21x(x – 1)² = 7x . 3(x² – 2x + 1) = 7x . (3x² – 6x + 3) nên nhân tử phụ của mẫu thức thứ nhất là 7x, ta nhân cả tử và mẫu của phân thức thứ nhất với nhân tử phụ 7x, ta được:

$\frac{2}{3x^2-6x+3}$$=\frac{2.7x}{\left(3x^2-6x+3\right).7x}$$=\frac{14x}{21x{\left(x-1\right)}^2}$

+ Vì 21x(x – 1)² = 3. 7x.(x – 1) . (x – 1) = 3(x – 1) . (7x² – 7x) nên nhân tử phụ của mẫu thức thứ hai là 3(x – 1), ta nhân cả tử và mẫu của phân thức thứ hai với nhân tử phụ 3(x – 1), ta được:

$\frac{3}{7x^2-7x}=\frac{3.3\left(x-1\right)}{\left(7x^2-7x\right).3\left(x-1\right)}=\frac{9\left(x-1\right)}{7x\left(x-1\right).3\left(x-1\right)}=\frac{9\left(x-1\right)}{21x{\left(x-1\right)}^2}$

Xem thêm