50 Bài tập Phân thức đại số (có đáp án)- Toán 8

Bài tập Toán 11 Chương 2 Bài 1: Phân thức đại số

A. Bài tập Phân thức đại số

I. Bài tập trắc nghiệm

Bài 1: Điều kiện xác định của phân thức$\frac{\left(x^2–4\right)}{\left(9x^2–16\right)}$ là ?

A. x = ± $\frac{4}{3}$.

B. x ≠ ± $\frac{4}{3}$.

C. – 43 < x < $\frac{4}{3}$.

D. x > $\frac{4}{3}$.

Lời giải:

Ta có điều kiện xác định của phân thức $\frac{\left(x^2–4\right)}{\left(9x^2–16\right)}$ là 9x² – 16 ≠ 0

⇔ 9x² ≠ 16 ⇔ x² ≠ $\frac{16}{9}$ ⇔ x ≠ ± $\frac{4}{3}$.

Chọn đáp án B.

Bài 2: Giá trị của x để phân thức  bằng 0 ?

A. x = ± 4.   

B. x ≠ 1.

C. x = -4.   

 

D. x = – 1.

Lời giải:

Để phân thức  bằng 0 ⇔

Chọn đáp án C.

Bài 3: Cặp phân thức nào không bằng nhau ?

Lời giải:

+ Ta có 

⇒ 16xy.3 = 24x.2y ⇔ $\frac{16xy}{24x}$ = $\frac{2y}{3}$.+ Ta có

⇒ 3.16xy = 2y.24x ⇔ $\frac{3}{24x}$ = $\frac{2y}{16xy}$.

+ Ta có

⇒ – 16xy.3 = – 2y.24x ⇔ $\frac{–16xy}{24x}$ = ( – 2y)3.

+ Ta có

⇒ – x2y.3y không bằng xy.3xy.

⇒ $\frac{–x2y}{3xy}$ không bằng $\frac{xy}{3y}$.

Chọn đáp án D.

Bài 4: Tìm biểu thức A sao cho : 

A. – 2x²y.   

B. x²y⁴.

C. – 2xy⁴.   

D. – x³y.

Lời giải:

Ta có:  ⇔ x2y3.( – 2xy2 ) = x2y.A

⇒ A= = – 2xy4.

Chọn đáp án C.

Bài 5: Biểu thức nào sau đây không phải là phân thức đại số ?

A. $\frac{1}{\left(x^2+1\right)}$

B. $\frac{\left(x+1\right)}{2}$

C. x² – 5

D. $\frac{\left(x+1\right)}{0}$

Lời giải:

Nhớ lại định nghĩa: Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng A/B, trong đó A, B là những đa thức và B khác đa thức 0.

+ $\frac{1}{\left(x^2+1\right)}$ có A = 1; B = x² + 1 ≠ 0 ⇒ $\frac{1}{\left(x^2+1\right)}$ là phân thức đại số.

+ $\frac{x+1}{2}$ có A = x + 1; B = 2 ≠ 0 ⇒ $\frac{x+1}{2}$ là phân thức đại số.

+ x² – 5 có A = x² – 5; B = 1 ⇒ x² – 5 là phân thức đại số.

+ $\frac{x+1}{0}$ có A = x + 1;B = 0 ⇒ $\frac{x+1}{0}$ không phải là phân thức đại số .

Chọn đáp án D.

Bài 6: Trong các phân thức sau phân thức nào bằng phân thức 

Lời giải:

Chọn đáp án A

Bài 7: Trong các phân thức sau , phân thức nào bằng phân thức 

Lời giải:

Chọn đáp án B

Bài 8: Tìm a để 

A. a = -2x     B. a =-x

C. a = -y     D. a = -1

Lời giải:

Chọn đáp án D

Bài 9: Tìm A để:

Lời giải:

Chọn đáp án C

Bài 10: Tìm A để: 

Lời giải:

Chọn đáp án A

Bài 11: Phân thức  có giá trị bằng 1 khi x bằng?

A. 1

B. 2

C. 3

D. -1

Lời giải

+ Điều kiện: 2x ≠ 0 ⇔ x ≠ 0.

+ Ta có  = 1 ⇒ x² + 1 = 2x ⇔ x² – 2x + 1 = 0

⇔ (x – 1)² = 0 ⇔ x – 1 = 0 ⇔ x = 1 (thỏa mãn)

Vậy x = 1.

Đáp án cần chọn là: A

Bài 12: Tìm x để phân thức ?

Lời giải

Đáp án cần chọn là: A

Bài 13: Có bao nhiêu giá trị của x để phân thức  có giá trị bằng 0?

A. 0

B. 2

C. 3

D. 1

Lời giải

+ Vì 11 ≠ 0 (luôn đúng) nên phân thức  luôn có nghĩa.

Vậy có hai giá trị của x thỏa mãn yêu cầu đề bài: x = 3; x = -3.

Đáp án cần chọn là: B

Bài 14: Giá trị của x để phân thức  có giá trị bằng 0 là?

A. x = 1             

B. x = -1

C. x = -1; x = 1  

D. x = 0

Lời giải

Vậy x = -1.

Đáp án cần chọn là: B

Bài 15: Phân thức nào dưới đây bằng với phân thức ?

Lời giải

Với (x, y ≠ 0) ta có 

Đáp án cần chọn là: D

II. Bài tập tự luận

Bài 1: Lập các cặp phân số bằng nhau từ 4 trong 6 số sau: -5; -3; -2; 6; 10; 15

Lời giải:

Học sinh sử dụng định nghĩa, tính chất hai phân thức bằng nhau để làm bài

Bài 2: Dùng định nghĩa hai phân thức bằng nhau, chứng minh các đẳng thức:

Lời giải:

a. 

Ta có:

b. 

Ta có:

Bài 3: Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức đa thức P trong các đẳng thức sau:

Lời giải:

a. Ta có: 

Thực hiện phép chia biểu đa thức cho đa thức ta được kết quả: 

b. Ta có: 

Bài 4: Tìm các số tự nhiên x, y biết rằng x, y là các số nguyên tố cùng nhau

Lời giải:

Ta có:

Do , x, y là số tự nhiên nên x = 5, y = 1

Bài 5. Cho ba đa thức : x² – 4x, x² + 4, x² + 4x. Hãy chọn đa thức thích hợp trong ba đa thức đó rồi điền vào chỗ trống trong đẳng thức dưới đây: $\frac{...}{\left(x^2–16\right)}=\frac{x}{x–4}$ 

Ta có: (…)(x – 4) = x(x² – 16) = x(x – 4)(x + 4) = (x² + 4x)(x -4)

Vậy phải điền vào chỗ trống đa thức x(x + 4) hay x² + 4x.

Bài 6. Ba phân thức sau có bằng nhau không?

$\frac{\left(x^2–2x+3\right)}{\left(x^2+x\right)}$ ;     $\frac{x–3}{x}$;      $\frac{\left(x^2–4x+3\right)}{\left(x^2–x\right)}$

Giải: 

Ta có: (x² – 2x – 3)x = x³ – 2x² – 3x

( x² + x)(x – 3) = x³ – 3x² + x² – 3x = x³ – 2x² – 3x

nên (x² – 2x – 3)x = ( x² + x)(x – 3)

do đó: $\frac{\left(x^2 – 2x – 3\right)}{(x^2+x)}$ = $\frac{\left(x–3\right)}{x}$

(x – 3)(x² – x) = x³ – x² + 3x² + 3x = x³ – 4x² + 3x

x(x²  – 4x + 3) = x³ – 4x² + 3x

nên (x – 3)(x² – x) = x(x²  – 4x + 3)

do đó  $\frac{\left(x–3\right)}{x}$ = $\frac{(x^2– 4x + 3)}{\left(x^2–x\right)}$

Vậy: $\frac{(x^2 – 2x – 3)}{\left(x^2+x\right)}$ = $\frac{\left(x–3\right)}{x}$ = $\frac{(x^2 – 4x + 3)}{(x^2 – x)}$

Bài 7: Rút gọn phân thức

a) $\frac{6x^5{y}^3}{3x^2{y}^2}$                                               b) $\frac{4x{y}^3{\left(x-y\right)}^2}{x^3-x^{2}y}$ 

c) $\frac{2x^2+xy-y^2}{x^2-x+xy-y}$                                    d) $\frac{x^3-y^3}{x^3+x^{2}y+x{y}^2}$ 

Giải

a) Ta có:  $\frac{6x^5{y}^3}{3x^2{y}^2}=\frac{\left(2x^{3}y\right)3x^2{y}^2}{3x^2{y}^2}=2x^{3}y$

b) Ta có:  $\frac{4x{y}^3{\left(x-y\right)}^2}{x^3-x^{2}y}=\frac{4y^3\left(x-y\right)x\left(x-y\right)}{xx\left(x-y\right)}=\frac{4y^3\left(x-y\right)}{x}$

c) Ta có: $\frac{2x^2+xy-y^2}{x^2-x+xy-y}=\frac{2x^2-xy+2xy-y^2}{x^2-x+xy-y}$

$=\frac{x\left(2x-y\right)+y\left(2x-y\right)}{x\left(x-1\right)+y\left(x-1\right)}=\frac{\left(2x-y\right)\left(x+y\right)}{\left(x-1\right)\left(x+y\right)}=\frac{2x-y}{x-1}$

d) Ta có:  $\frac{x^3-y^3}{x^3+x^{2}y+x{y}^2}=\frac{\left(x-y\right)\left(x^2+xy+y^2\right)}{x\left(x^2+xy+y^2\right)}=\frac{x-y}{x}$

Bài 8: Rút gọn phân thức

a) $\frac{x-y}{y^2-x^2}$                                              b) $\frac{4x^3\left(4-x^2\right)}{x^3-2x^2}$ 

c) $\frac{2x^2-5x+2}{-x^2+3x-2}$                                       d) $\frac{2x^2-8x+8}{x^3-8}$ 

Giải

a) Ta có: $\frac{x-y}{y^2-x^2}=\frac{-\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}=\frac{-1}{y+x}$

b) Ta có: $\frac{4x^3\left(4-x^2\right)}{x^3-2x^2}=\frac{4x^3\left(2-x\right)\left(2+x\right)}{x^2\left(x-2\right)}$

$=\frac{-4x^3\left(x-2\right)\left(2+x\right)}{x^2\left(x-2\right)}=-4x\left(2+x\right)$

c) Ta có: $\frac{2x^2-5x+2}{-x^2+3x-2}=\frac{2x^2-4x-x+2}{2x-x^2-2+x}=\frac{2x\left(x-2\right)-\left(x-2\right)}{x\left(2-x\right)-\left(2-x\right)}$ $=\frac{\left(2x-1\right)\left(x-2\right)}{\left(x-1\right)\left(2-x\right)}=\frac{2x-1}{-\left(x-1\right)}=\frac{2x-1}{1-x}$

d) Ta có: $\frac{2x^2-8x+8}{x^3-8}=\frac{2\left(x^2-4x+4\right)}{x^3-2^3}$

 $=\frac{2{\left(x-2\right)}^2}{\left(x-2\right)\left(x^2+2x+4\right)}=\frac{2\left(x-2\right)}{\left(x^2+2x+4\right)}$

Bài 9

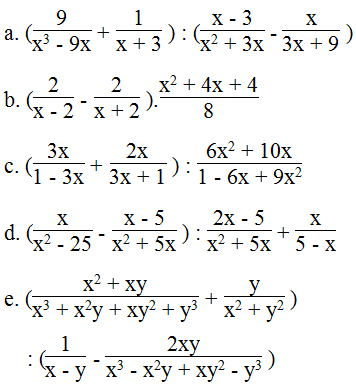
Lời giải:

a.

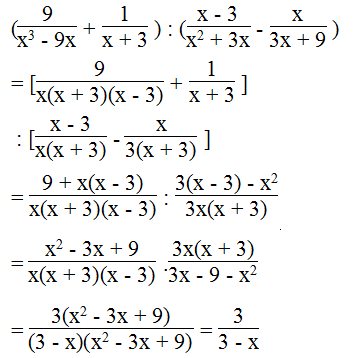
b.

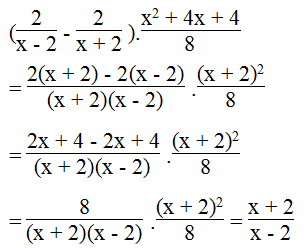
c.

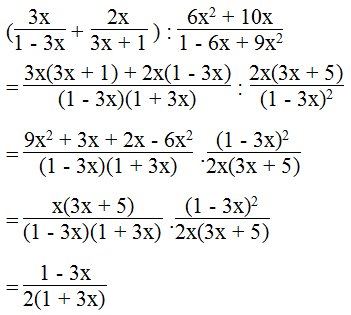
d.

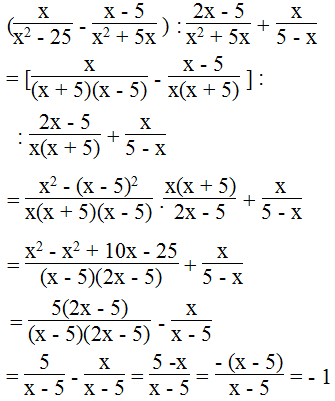
e.

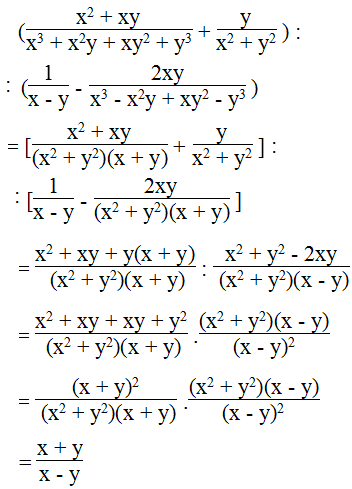
Bài 10

Chứng minh đẳng thức:

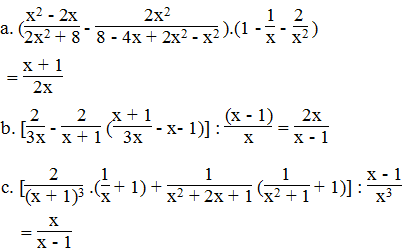
Lời giải:

a. Ta có:

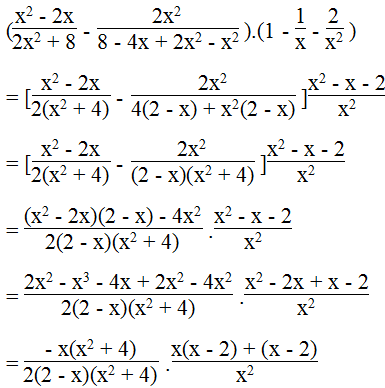
Vế trái bằng vế phải nên đẳng thức được chứng minh.

b. Ta có:

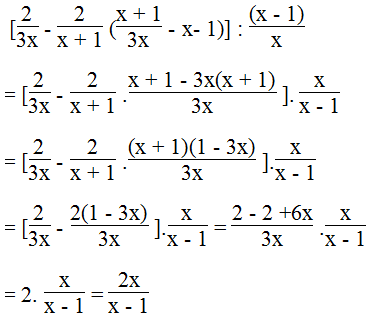
Vế trái bằng vế phải nên đẳng thức được chứng minh.

c. Ta có:

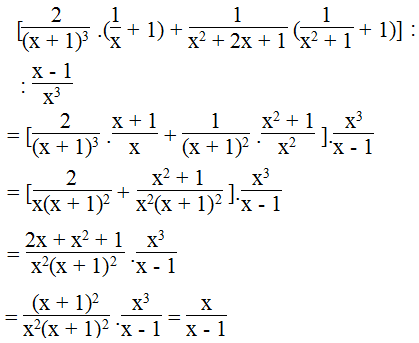
Vế trái bằng vế phải nên đẳng thức được chứng minh.

III. Bài tập vận dụng

1. Thực hiện các phép tính sau :

a)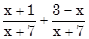                                                     

b)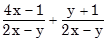 

c)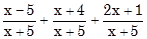                                       

d) .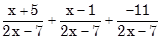

2. Thực hiện các phép tính sau :

a)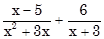                                                

b) x + 2 + .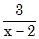

3. Thực hiện các phép tính sau :

a)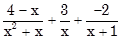                                             

b) .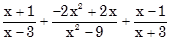

4. Thực hiện các phép tính :

a)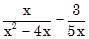                                                     

b) .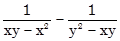

5. Tìm x :

a) x + 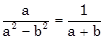 (a, b là hằng số)

b) x – 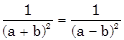 (a, b là hằng số).

6. Thực hiện phép tính :

a)  +  +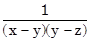 

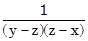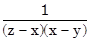
b)  +  +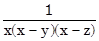 

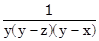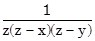
c)  +  + .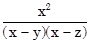

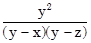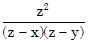7. Thực hiện phép tính :

a)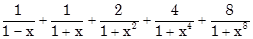 

b)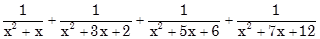 

c) .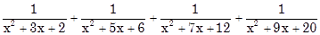

8. a) Cho biết 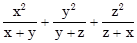 = 2009

Tính .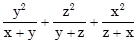

b) Cho x, y, z là ba số thoả mãn xyz = 2. Tính giá trị của biểu thức :

 +  + 

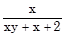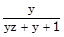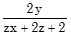
9. Tìm a, b biết :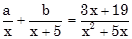 

10. Cho 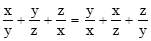. Chứng minh rằng trong ba số x, y, z tồn tại hai số bằng nhau.

B. Lý thuyết Phân thức đại số

1. Định nghĩa

Một phân thức đại số (hay nói gọn là phân thức) là một biểu thức có dạng $\frac{A}{B}$,

trong đó A, B là những đa thức và B khác đa thức 0.

Trong đó:

+ A được gọi là tử thức (hay gọi là tử).

+ B được gọi là mẫu thức (hay gọi là mẫu).

Chú ý:

+ Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.

+ Số 0, số 1 cũng là một phân thức đại số.

Ví dụ. Ta có các phân thức đại số

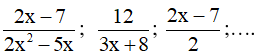
2. Hai phân thức bằng nhau

Hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$ gọi là bằng nhau nếu A . D = B . C. Ta viết:

$\frac{A}{B}=\frac{C}{D}$ nếu A . D = B . C.

Ví dụ.

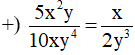 vì 5x²y . 2y³ = 10xy⁴ . x  (do cùng bằng 10 x²y⁴).

vì x . (2x + 4) = 2 . (x² + 2x) (do cùng bằng 2x² + 4x).

Xem thêm