Lý thuyết Toán lớp 11 Bài 1: Dãy số
A. Lý thuyết Dãy số
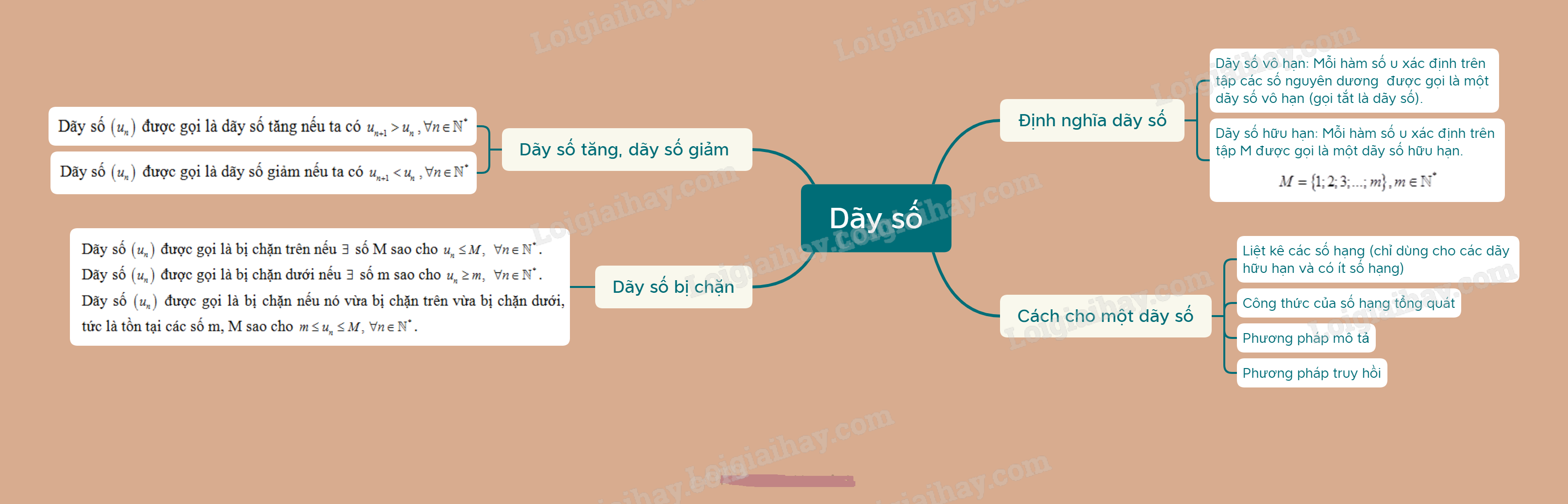
1. Định nghĩa dãy số
– Hàm số u xác định trên tập các số nguyên dương được gọi là một dãy số vô hạn (gọi tắt là dãy số), nghĩa là
Dãy số trên được kí hiệu là .
– Dãy số được viết dưới dạng khai triển
– Số là số hạng đầu; là số hạng thứ n và gọi là số hạng tổng quát của dãy số.
*Chú ý: Nếu thì được gọi là dãy số không đổi.
Mỗi hàm số u xác định trên tập được gọi là một dãy số hữu hạn.Dạng khai triển của dãy số hữu hạn là .
Trong đó, số gọi là số hạng đầu, là số hạng cuối.
2. Cách cho một dãy số
Một dãy số có thể cho bằng:
– Liệt kê các số hạng (với các dãy hữu hạn).
– Công thức của số hạng tổng quát .
– Phương pháp truy hồi:
+) Cho số hạng thứ nhất (hoặc một vài số hạng đầu tiên)
+) Cho một công thức tính theo (hoặc theo vài số hạng đứng ngay trước nó).
– Phương pháp mô tả.
3. Dãy số tăng, dãy số giảm
Dãy số được gọi là dãy số tăng nếu ta có .
Dãy số được gọi là dãy số giảm nếu ta có .
4. Dãy số bị chặn
Dãy số được gọi là bị chặn trên nếu số M sao cho .
Dãy số được gọi là bị chặn dưới nếu số m sao cho .
Dãy số được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho .
B. Bài tập Dãy số
Đang cập nhật …
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 5: Phương trình lượng giác cơ bản
Lý thuyết Bài 1: Dãy số
Lý thuyết Bài 2: Cấp số cộng
Lý thuyết Bài 3: Cấp số nhân
Lý thuyết Bài 1: Giới hạn của dãy số
Lý thuyết Bài 2: Giới hạn của hàm số
Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác
Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Lý thuyết Chương 3: Giới hạn. Hàm số liên tục
==== ~~~~~~ ====