Hình nào trong các hình dưới đây chứa đồ vật có dạng hình thoi?

Câu hỏi:

Hình nào trong các hình dưới đây chứa đồ vật có dạng hình thoi?

Trả lời:

Hướng dẫn giải:
Hình 1 có các giá treo đồ có dạng hình thoi.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Hình thoi (mới 2023 + bài tập) – Toán 8
   Lý thuyết Hình thoi

   A. Lý thuyết

   1. Định nghĩa

   Hình thoi là tứ giác có bốn cạnh bằng nhau.

   Hình thoi cũng là một hình bình hành.

   

   Tổng quát: ABCD là hình thoi \Leftrightarrow AB = BC = CD = DA

   2. Tính chất

   Hình thoi có tất cả các tính chất của hình bình hành.

   Định lí: Trong hình thoi:

   + Hai đường chéo vuông góc với nhau.

   + Hai đường chéo là các đường phân giác các góc của hình thoi.

   3. Dấu hiệu nhận biết hình thoi

   + Tứ giác có bốn cạnh bằng nhau là hình thoi.

   + Hình bình hành có hai cạnh kề bằng nhau là hình thoi

   + Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

   + Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

   Ví dụ: Cho hình chữ nhật ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD. Chứng minh tứ giác MNPQ là hình thoi.

   Hướng dẫn:

   

   M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD

   ⇒ AM = MB; BN = NC; CP = DP; AQ = DQ

   + Xét Δ ABD có

   ⇒ MQ là đường trung bình của Δ ABD.

   ⇒ QM = 1/2BD = 1/2AC       ( 1 )

   + Xét Δ ABC có

   ⇒ MN là đường trung bình của Δ ABC.

   ⇒ MN = 1/2BD = 1/2AC       ( 2 )

   + Xét Δ BCD có

   ⇒ NP là đường trung bình của Δ BCD.

   ⇒ NP = 1/2BD = 1/2AC       ( 3 )

   + Xét Δ ADC có

   ⇒ QP là đường trung bình của Δ ADC.

   ⇒ QP = 1/2BD = 1/2AC       ( 4 )

   Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.

   ⇒ MNPQ là hình thoi.

   B. Bài tập tự luyện

   Bài 1: Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đội cạnh đó. Tính các góc của hình thoi.

   Hướng dẫn:

   

   Gọi H là chân đường cao kẻ từ đỉnh A xuống cạnh CD, theo giả thiết ta có:

    ⇒ AH là đường trung trực của đoạn CD nên AC = AD       ( 1 )

   Áp dụng định nghĩa của hình thoi ABCD, ta có

   AD = AB = BC = CD       ( 2 )

   Từ ( 1 ) và ( 2 ) ta có AD = AC = CD ⇒ Δ ACD là tam giác đều

   ⇒ ADCˆ = 60⁰.

   Vì góc A và góc D là hai góc trong cùng phía của AB//CD nên chúng bù nha.

   Hay Aˆ + Dˆ = 180⁰ ⇒ Aˆ = 180⁰ – Dˆ = 180⁰ – 60⁰ = 120⁰.

   Áp dụng tính chất về góc của hình thoi ta có:

   Bài 2: Chứng minh rằng các đường cao của hình thoi bằng nhau.

   

   Hướng dẫn:

   Xét hình thoi ABCD, kẻ hai đường cao

   AH ⊥ BC, AK ⊥ CD.

   Ta cần chứng minh: AH = AK.

   Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:

    ⇒ Δ ABH = Δ ADH ( g – c – g )

   ⇒ AH = AK (cặp cạnh tương ứng bằng nhau)

   → (đpcm)
2. Giải SGK Toán 8 Bài 11: Hình thoi
   Giải bài tập Toán lớp 8 Bài 11: Hình thoi

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 104 Toán 8 Tập 1: Chứng minh rằng tứ giác ABCD trên Hình 100 cũng là một hình bình hành.

   

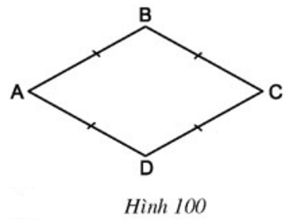
   Lời giải

   Tứ giác ABCD có các cặp cạnh đối bằng nhau

   ⇒ ABCD là hình bình hành

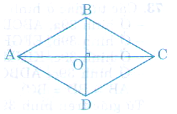
   Câu hỏi 2 trang 104 Toán 8 Tập 1: Cho hình thoi ABCD, hai đường chéo cắt nhau tại O (h.101).

   a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất gì?

   b) Hãy phát hiện thêm các tính chất khác của hai đường chéo AC và BD.

   

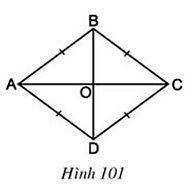
   Lời giải

   a) Vì hình thoi có tất cả các tính chất của hình bình hành nên theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất cắt nhau tại trung điểm mỗi đường

   b) Xét ΔAOB và ΔCOB

   AB = CB

   BO chung

   OA = OC (O là trung điểm AC )

   ⇒ ΔAOB = ΔCOB (c.c.c)

   ⇒ $\widehat{AOB}=\widehat{COB},\widehat{ABO}=\widehat{CBO}$ (các cặp góc tương ứng)

   Với $\widehat{AOB}=\widehat{COB}$

   Mà $\widehat{AOB}+\widehat{COB}=180°$

   $\Rightarrow \widehat{AOB}=\widehat{COB}=\frac{180°}{2}=90°\Rightarrow AC\perp BD$

   Nếu $\widehat{ABO}=\widehat{CBO}$

   $\Rightarrow$AC là phân giác của góc $\widehat{ABC}$

   Chứng minh tương tự, ta kết luận được:

   AC, BD là các đường phân giác của các góc của hình thoi và AC ⊥ BD tại O

   Câu hỏi 3 trang 105 Toán 8 Tập 1: Hãy chứng minh dấu hiệu nhận biết 3.

   Lời giải

   Dấu hiệu nhận biết 3: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi

   

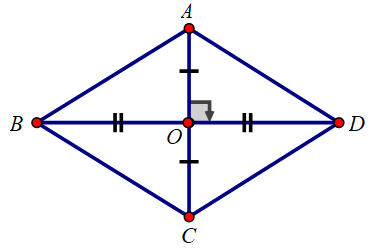
   ABCD là hình bình hành ⇒ O là trung điểm AC và O là trung điểm BD

   Xét $\Delta AOB$ và $\Delta AOD$ có:

   $\widehat{AOB}=\widehat{AOD}=90°$

   OA chung

   OB = OD (O là trung điểm BD)

   ⇒ ΔAOB = ΔAOD (hai cạnh góc vuông)

   ⇒ AB = AD (hai cạnh tương ứng)

   Hình bình hành ABCD ⇒ AB = CD và AD = BC

   Do đó AB = BC = CD = DA

   ⇒ ABCD là hình thoi.

   Bài tập (trang 105, 106)

   Bài 73 trang 105 Toán 8 Tập 1: Tìm các hình thoi trên hình 102.

   

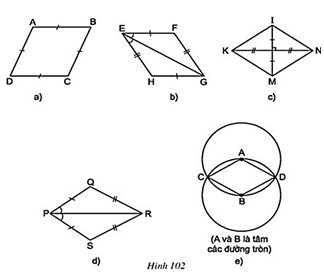
   Lời giải:

   Các tứ giác ở hình 102a, b, c, e là hình thoi.

   – Hình 102a:

   Tứ giác ABCD là hình thoi vì có AB = BC = CD = DA

   – Hình 102b:

   Xét tứ giác EFGH, ta có:

   EF = GH và EH = FG

   ⇒ EFGH là hình bình hành

   Lại có EG là tia phân giác của $\widehat{\text{HEF}}$

   ⇒ EFGH là hình thoi. (Dấu hiêu 4).

   – Hình 102c:

   Xét tứ giác KINM, ta có:

   Hai đường chéo IM, KN cắt nhau tại trung điểm mỗi đường.

   ⇒ IKMN là hình bình hành

   Lại có IM ⊥ KN

   ⇒ IKMN là hình thoi. (Dấu hiệu 3).

   – Hình 102e:

   Xét tứ giác ADBC là hình thoi vì:

   AC = AD = AB (C, B, D cùng thuộc đường tròn tâm A).

   BC = BA = BD (A, C, D cùng thuộc đường tròn tâm B)

   ⇒ AC = CB = BD = DA

   ⇒ ACBD là hình thoi.

   – Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.

   Bài 74 trang 106 Toán 8 Tập 1: Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

   A. 6cm;        

   B. $\sqrt{41}$ cm;        

   C. $\sqrt{164}$ cm;        

   D. 9 cm.

   Lời giải:

   

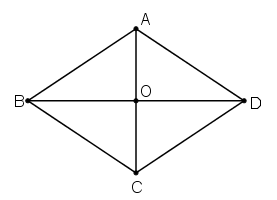
   Giả sử ta có hình thoi ABCD thỏa mãn yêu cầu bài toán, trong đó đường chéo AC = 8cm, BD = 10cm.

   Gọi ABCD O là giao điểm hai đường chéo

   ⇒ O là trung điểm của AC và BD.

   $\Rightarrow OA=OC=\frac{AC}{2}=\frac{8}{2}=4cm$

   $\Rightarrow OB=OD=\frac{BD}{2}=\frac{10}{2}=5cm$

   Xét vuông tại O, ta có:

   $A{B}^2=O{B}^2+O{A}^2$

   $=4^2+5^2=16+25=41$ (định lý Py – ta – go)

   $\Rightarrow AB=\sqrt{41}cm.$

   Vậy chọn đáp án là B.

   Bài 75 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.

   Lời giải:

   

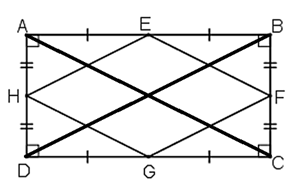
   +) Xét tam giác ABD có:

   E là trung điểm của AB

   H là trung điểm của AD

   ⇒ EH là đường trung bình của tam giác ADB

   $\Rightarrow EH=\frac{BD}{2}$(1)

   +) Xét tam giác ABC có:

   E là trung điểm của AB

   F là trung điểm của BC

   ⇒ EF là đường trung bình của tam giác ABC

   $\Rightarrow EF=\frac{AC}{2}$(2)

   +) Xét tam giác BCD có:

   F là trung điểm của BC

   G là trung điểm của DC

   ⇒ FG là đường trung bình của tam giác BCD

   $\Rightarrow FG=\frac{BD}{2}$(3)

   +) Xét tam giác CDA có:

   H là trung điểm của AD

   G là trung điểm của DC

   ⇒ HG là đường trung bình của tam giác CDA

   $\Rightarrow HG=\frac{AC}{2}$(4)

   Ta lại có ABCD là hình chữ nhật nên AC = BD (5)

   Từ (1), (2), (3), (4) và (5) suy ra EF = FG = GH= HE

   ⇒Tứ giác EFGH là hình thoi.

   Bài 76 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

   Lời giải:

   

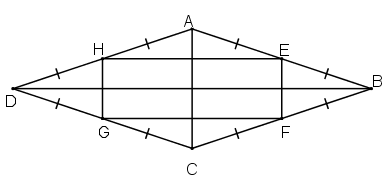
   +) Xét tam giác ABC có:

   E là trung điểm của AB

   F là trung điểm của BC

   ⇒ EF là đường trung bình của tam giác ABC

   $\Rightarrow EF//AC,EF=\frac{AC}{2}$(1)

   +) Xét tam giác CDA có:

   H là trung điểm của AD

   G là trung điểm của DC

   ⇒ HG là đường trung bình của tam giác CDA

   $\Rightarrow HG//AC,HG=\frac{AC}{2}$(2)

   Từ (1) và (2) suy ra EF // HG và EF = HG

   ⇒Tứ giác EFGH là hình bình hành

   Ta lại có:

   EF // AC

   BD ⊥ AC

   Suy ra BD ⊥ EF (3)

   Xét tam giác ABD có:

   E là trung điểm của AB

   H là trung điểm của AD

   ⇒ EH là đường trung bình của tam giác ADB

   $\Rightarrow EH//BD$ (4)

   Từ (3) và (4) suy ra: EF ⊥ EH

   $\Rightarrow \widehat{FEH}=90°$

   Hình bình hành EFGH có $\widehat{FEH}=90°$ nên là hình chữ nhật

   Bài 77 trang 106 Toán 8 Tập 1:Chứng minh rằng:

   a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

   b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

   Lời giải:

   

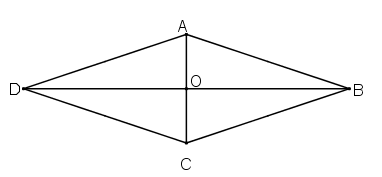
   a) Gọi O là giao điểm của hai đường chéo của hình thoi ABCD

   Vì ABCD là hình thoi nên ABCD là hình bình hành

   Mà tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.

   Suy ra O là tâm đối xứng của hình thoi ABCD.

   b)

   

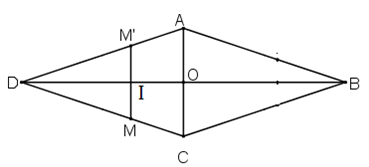
   Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.

   * Ta chứng minh: đường chéo BD là trục đối xứng của hình

   Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.

   Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi

   + Gọi I là giao điểm của MM’ và BD.

   Xét tam giác DIM và DIM’ có:

   $\widehat{DIM}=\widehat{DIM‘}=90°$

   DI chung

   IM= IM’ ( do M và M’ đối xứng với nhau qua BD)

   $\Rightarrow$∆DIM = ∆DIM’ ( c.g.c)

   $\Rightarrow \widehat{IDM}=\widehat{IDM‘}$ và DM = DM’

   Lại có: ABCD là hình thoi nên $\widehat{IDA}=\widehat{IDC}$ (DB là phân giác $\widehat{ADC}$) hay $\widehat{IDA}=\widehat{IDM}$

   Mà $\widehat{IDM}=\widehat{IDM‘}$

   $\Rightarrow \widehat{IDA}=\widehat{IDM‘}$

   Suy ra điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi

   Do đó BD là trục đối xứng của hình thoi.

   Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.

   Vậy hai đường chéo AC, BD là hai trục đối xứng của hình thoi.

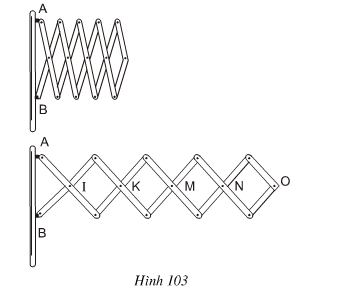
   Bài 78 trang 106 Toán 8 Tập 1: Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng?

   

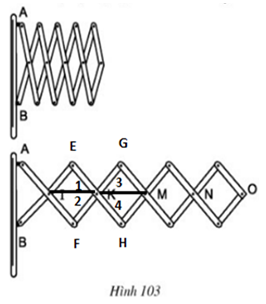
   Lời giải:

   Ta có hình vẽ minh họa như sau:

   

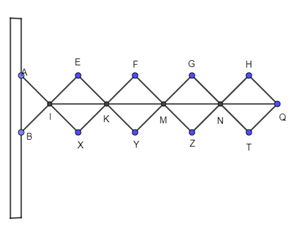
   Tứ giác IEKX là hình thoi nên KI là phân giác $\widehat{EKX}$

   Tứ giác KFMY là hình thoi nên KM là phân giác $\widehat{FKX}$

   Mà $\widehat{EKX}=\widehat{FKY}$ (hai góc đối đỉnh) 

   Suy ra KI trùng KM

   Suy ra K, I, M thẳng hàng (1).

   Tứ giác KFMY là hình thoi nên MK là phân giác $\widehat{FMY}$

   Tứ giác MGNZ là hình thoi nên MN là phân giác $\widehat{GMZ}$

   Mà $\widehat{GMZ}=\widehat{FMY}$ (hai góc đối đỉnh)

   Suy ra MK trùng MN

   Suy ra K, M, N thẳng hàng (2).

   Tứ giác MGNZ là hình thoi nên NM là phân giác $\widehat{GNZ}$

   Tứ giác HQTN là hình thoi nên NQ là phân giác $\widehat{HNT}$

   Mà $\widehat{GNZ}=\widehat{HNT}$ (hai góc đối đỉnh)

   Suy ra NM trùng NQ

   Suy ra Q, M, N thẳng hàng (3).

   Từ (1), (2) và (3) suy ra các điểm I, K, M, N, O cùng nằm trên một đường thẳng.
3. Dấu hiệu nhận biết hình thoi chi tiết, đầy đủ 2023
   Hình thoi là tứ giác có bốn cạnh bằng nhau, là hình bình hành đặc biệt với hai cạnh kề bằng và hai đường chéo vuông góc với nhau.

   Trong hình thoi:

   – Các góc đối nhau bằng nhau;

   – Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

   – Hai đường chéo là các đường phân giác của các góc của hình thoi;

   – Hình thoi có tất cả tính chất của hình bình hành.

   2. Dấu hiệu nhận biết hình thoi

   Để có thể giải các bài tập liên quan đến hình thoi cần nắm được Dấu hiệu nhận biết hình thoi như sau:

   – Tứ giác có bốn cạnh bằng nhau;

   – Hình bình hành có hai cạnh kề bằng nhau;

   – Hình bình hành có hai đường chéo vuông góc nhau;

   – Hình bình hành có một đường chéo là đường phân giác của một góc.

   3. Công thức tính diện tích hình thoi

   Dấu hiệu nhận biết hình thoi đã được giải đáp ở trên theo đó công thức tính diện tích hình thoi như sau: Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo.

   S= ½ (d₁ x d₂)

   4. Công thức tính chu vi hình thoi

   Chu vi của hình thoi bằng độ dài một cạnh nhân với 4:

   P = a x 4

   5. Các cách để chứng minh tứ giác là hình thoi

   Để chứng minh tứ giác là hình thoi cần nắm được Dấu hiệu nhận biết hình thoi và có thể áp dụng một trong số những cách chứng minh sau đây.

   – Chứng minh tứ giác có 2 đường chéo là đường trung trực của nhau:

   Ví dụ: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi.

   Theo bài ra, ta có:

   ΔABC cân tại A có trung tuyến AM

   => AM đồng thời là đường trung trực của BC

   => Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau.

   – Chứng minh tứ giác có bốn cạnh bằng nhau

   Ví dụ: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

   Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD

   => EH là đường trung bình của tam giác

   => EH = 1/2 BD (1)

   Chứng minh tương tự ta có: EF = ½ AC; FG = ½ BD; HG = ½ AC (2)

   Vì ABCD là hình chữ nhật nên AC = BD (3)

   Từ (1), (2) và (3), ta suy ra EH = EF = HG = GF

   => Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau. (đ.p.c.m)

   – Chứng minh tứ giác là hình bình hành có hai đường chéo vuông góc

   Ví dụ: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong của các tam giác AOB; BOC; COD và DOA là đỉnh của một hình thoi.

   Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.

   Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.

   Xét ΔBMO và ΔDPO có:

   Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)

   => ΔBMO = ΔDPO (g. c. g)

   => OM = OP và các điểm M, O, P thẳng hàng (6)

   Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (7)

   Từ (6) và (7) Suy ra: Tứ giác MNPQ là hình bình hành do các đường chéo cắt nhau tại trung điểm mỗi đường. (8)

   Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON. (9)

   Từ (8) và (9) suy ra: MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc. (đ.p.c.m)

   – Chứng minh tứ giác là hình bình hành có hai cạnh kề bằng nhau

   Ví dụ: Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: IMNK là hình thoi.

   Theo giả thiết ta có: M là trung điểm của BE và I là trung điểm của DE

   => MI là đường trung bình của ΔBDE

   => MI // BD và MI = 1/2 BD

   Chứng minh tương tự, ta có:

   NK // BD và NK= 1/2 BD

   Do có MI // NK và MI = NK nên tứ giác MINK là hình bình hành (4)

   Chứng minh tương tự, ta có: IN là đường trung bình của ΔCDE

   => IN = 1/2 CE mà CE = BD (gt) => IN = IM (5)

   Từ (4) và (5) suy ra Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau.

   6. Bài tập liên quan đến hình thoi

   Ví dụ 1 : Cho hình thoi ABCD có AB = BC = CD = DA = 5cm. Tính diện tích hình thoi.

   Hướng dẫn giải:

   Áp dụng công thức ta có chu vi hình thoi ABCD là:

   P = 4.5 = 20(cm)

   Ví dụ 2: Trong các hình sau, hình nào là hình thoi? Vì sao?

   

   Hướng dẫn:

   a) Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi

   b) Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành.

   Hình bình hành ABCD có đường chéo AC là đường phân giác góc  nên ABCD là hình thoi.

   c) Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi

   d) Ta có: B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD (1)

   A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD (2)

   Từ (1) và (2) suy ra, AC = AD = BC = BD

   Do đó, ABCD là hình thoi.

   e) Tứ giác ABCD có các cạnh đối diện không bằng nhau, do đó ABCD không là hình thoi.

   Ví dụ 3:

   Tìm các hình thoi trên hình 102.

   

   

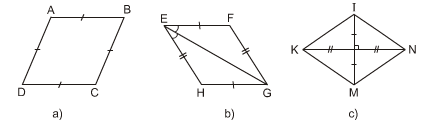
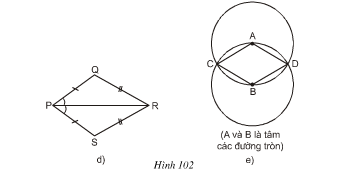
   Lời giải:

   Các tứ giác ở hình 102a, b, c, e là hình thoi.

   – Hình 102a: ABCD là hình thoi (theo định nghĩa)

   – Hình 102b: EFGH là hình thoi (theo dấu hiệu nhận biết 4)

   – Hình 102c: KINM là hình thoi (theo dấu hiệu nhận biết 3)

   – Hình 102e: ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)

   Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.

   Ví dụ 4: Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

   A. 6cm;       B. √41 cm ;        c) √164cm ;          d) 9cm

   Lời giải:

   Xét bài toán tổng quát:

   ABCD là hình_thoi, O là giao điểm hai đường chéo.

   Theo định lí Pitago ta có:

   

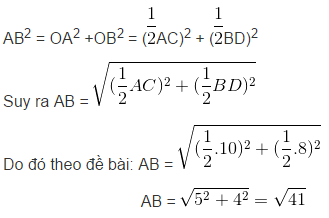
   Vậy B đúng

   Ví dụ 5:

   Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình_thoi.

   

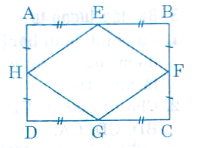
   Lời giải:

    Ta có: AE = BE = ½.AB

   DG = GC = ½.DC

   Mà AB = DC (ABCD là hình chữ nhật)

   => AE = BE = DG = GC.

   Chứng minh tương tự ta có AH = HD = FB = FC

   Xét ΔEAH và ΔGDH có:

   AE = DG; 

   AH = HD

   => ΔEAH = ΔGDH => HE = HG.

   Chứng minh tương tự ta có: EH = EF = GH = GF

   Vậy EFGH là hình thoi (theo định nghĩa)

   Ví dụ 6: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

   Lời giải:

    

   

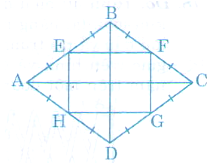
   Ta có: EB = EA, FB = FA (gt)

   Nên EF là đường trung bình của ΔABC.

   Do đó EF // AC

   HD = HA, GD = GC (gt) nên HG là đường trung bình của ΔADC.

   Do đó HG // AC

   Suy ra EF // HG (1)

   Chứng minh tương tự EH // FG (2)

   Từ (1) và (2) ta được EFGH là hình bình hành

   Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF

   EH // BD và EF ⊥ BD nên EF ⊥ EH

   Nên Hình bình hành EFGH có góc E = 90^o nên là hình chữ nhật

   Ví dụ 7:  Chứng minh rằng:

   a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.

   b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.

   Lời giải:

   a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.

   Hình thoi cũng là một hình bình hành nên giao điểm của hai đường chéo hình thoi là tâm đối xứng của hình.

   b) 

   

   – BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.

   – Mọi điểm trên BD đều đối xứng qua chính đường thẳng BD. (*)

   – Tâm O là tâm đối xứng mà O ∈ BD

   => BD là trục đối xứng của hình thoi. (**)

   – Tương tự AC cũng là là trục đối xứng của hình thoi.

   ((*) Điểm đối xứng của điểm B qua BD chính là điểm B.

   (**) Định nghĩa trục đối xứng: Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.)

   Ví dụ 8:  Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bàng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hìnhthoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng ?

   

    

   

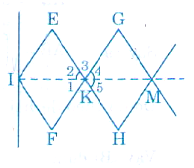
   Lời giải:

   Các tứ giác IEKF, KGMH là hình thoi nên KI là phân giác của góc EKF, KM là phân giác của góc GKH.

   Suy ra I, K, M thẳng hàng.

   Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.

   Lưu ý: Để chứng minh 3 điểm thẳng hàng, ta có thể chứng minh tổng 3 góc kề nhau bằng 180^o.

    
    

    

   7. Một số lưu ý khi làm về bài tập hình thoi

   Bài tập về hình thoi gồm những dạng bài tập như sau:

   – Chứng minh một hình là hình thoi.

   – Tính chu vi hình thoi.

   – Tính diện tích hình thoi.

   Những lưu ý khi làm bài tập về hình thoi cần biết đó là cần phải nắm vững các kiến thức về dấu hiệu, tính chất cũng như công thức tính chu vi và diện tích hình thoi. Từ đó có thể áp dụng vào việc giải các bài tập từ cơ bản đến nâng cao.

   Khi nhận biết những dấu hiệu như thế nào là hình thoi thì việc chứng minh trong toán hình sẽ trở nên đơn giản và dễ dàng hơn.
4. Giải SGK Toán 8 Bài 7: Hình bình hành
   Giải bài tập Toán lớp 8 Bài 7: Hình bình hành

   Trả lời câu hỏi giữa bài

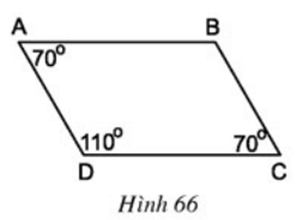
   Câu hỏi 1 trang 90 Toán 8 Tập 1: Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?

   

   Lời giải

   Ta sử dụng thước thẳng đo các cặp cạnh đối AB và CD; AD và BC ta thấy các cặp cạnh này song song và bằng nhau.

   Như vậy các cạnh đối của tứ giác ABCD song song và bằng nhau.

   (Nhận xét trang 70: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau).

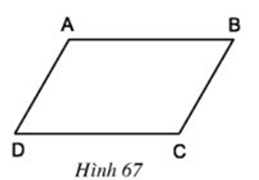
   Câu hỏi 2 trang 90 Toán 8 Tập 1: Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.

   

   Lời giải

   Sau khi quan sát, ta dự đoán hình bình hành ABCD có các tính chất sau:

   – Các cạnh đối bằng nhau

   – Các góc đối bằng nhau

   – Hai đường chéo cắt nhau tại trung điểm mỗi đường.

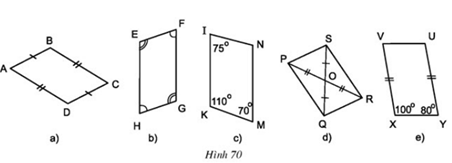
   Câu hỏi 3 trang 92 Toán 8 Tập 1: Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?

   

   Lời giải

   Hình 70a):

   Xét tứ giác ABCD, có:

   AB = DC

   AD = BC

   Suy ra tứ giác ABCD là hình bình hình (các cạnh đối bằng nhau).

   Hình 70b):

   Xét tứ giác EFGH, có:

   $\widehat{E}=\widehat{G}\widehat{H}=\widehat{F}$

   Suy ra EFGH là hình bình hành (các góc đối bằng nhau).

   Hình 70c):

   Xét tứ giác MNIK, có:

   $\widehat{K}+\widehat{M}={110}^0+{70}^0={180}^0\Rightarrow$MN//IK (hai góc trong cùng phía bù nhau)

   $\widehat{K}+\widehat{I}={110}^0+{75}^0={185}^0\Rightarrow$IN và KM không song song

   Suy ra MNIK là hình thang không phải hình bình hành.

   Hình 70d):

   Xét tứ giác PQRS, có:

   Hai đường chéo cắt nhau tại trung điểm mỗi đường nên tứ giác PQRS là hình bình hành.

   Hình 70e):

   Xét tứ giác XYUV, có:

   $\widehat{X}+\widehat{Y}={100}^0+{80}^0={180}^0$

   Mà hai góc ở vị trí trong cùng phía nên XY // UV

   Mặt khác XY = UV

   Nên tứ giác XYUV là hình bình hành.

   Bài tập (trang 92, 93)

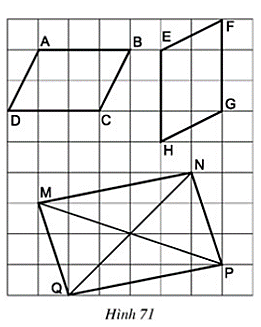
   Bài 43 trang 92 Toán 8 Tập 1: Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

   

   Lời giải: 

   Xét tứ giác ABCD, có:

   AB = CD ( = 3 ô)

   AB // CD

   Suy ra tứ giác ABCD là hình bình hành.

   Xét tứ giác EFGH, có:

   EH // FG

   EH = FG (= 3 ô)

   Suy ra tứ giác EFGH là hình bình hành

   Xét tứ giác MNPQ có:

   MN = PQ

   MQ = NP

   Suy ra tứ giác MNPQ là hình bình hành

   Bài 44 trang 92 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

   Lời giải:

   

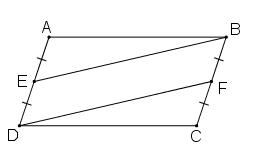
   Cách 1: Sử dụng phương pháp chứng minh hai tam giác bằng nhau:

   Vì ABCD là hình bình hành nên:

   AB = CD (hai cạnh đối bằng nhau)

   $\widehat{A}=\widehat{C}$(hai góc đối bằng nhau)

   AD = BC $\Rightarrow$ AE = ED = BF = CF (E là trung điểm của AD, F là trung điểm của BC).

   Xét $\Delta ABE$ và $\Delta CDF$, có:

   AB = CD (cmt)

   $\widehat{A}=\widehat{C}$ (cmt)

   AE = CF (cmt)

   ⇒ ΔAEB = ΔCFD (c.g.c)

   ⇒ EB = DF (hai cạnh tương ứng).

   Cách 2: Sử dụng phương pháp chứng minh tứ giác BEDF là hình bình hành

   Vì ABCD là hình bình hành

   ⇒ AD//BC hay DE // BF và AD = BC.

   Ta có: E là trung điểm của AD ⇒$DE=\frac{AB}{2}$

   F là trung điểm của BC ⇒$BF=\frac{BC}{2}$

   Mà AD = BC

   ⇒ DE = BF.

   Xét tứ giác BEDF có:

   DE // BF và DE = BF

   ⇒ BEDF là hình bình hành

   ⇒ BE = DF.

   Bài 45 trang 92 Toán 8 Tập 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

   a) Chứng minh rằng DE // BF

   b) Tứ giác DEBF là hình gì? Vì sao?

   Lời giải

   

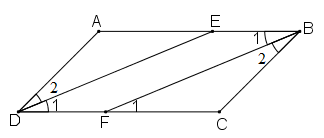
   a) Ta có: $\widehat{D_1}=\widehat{D_2}=\frac{1}{2}\widehat{ADC}$ (DE là phân giác của $\widehat{ADC}$)

   Ta lại có: $\widehat{B_1}=\widehat{B_2}=\frac{1}{2}\widehat{ABC}$(BF là phân giác của $\widehat{ABC}$)

   Mà $\widehat{ADC}=\widehat{ABC}$ (ABCD là hình bình hành)

   $\Rightarrow \widehat{D_1}=\widehat{B_1}$(1)

   Vì ABCD là hình bình hành ⇒ AB // CD ⇒ $\widehat{B_1}=\widehat{F_1}$ (Hai góc so le trong) (2)

   Từ (1) và (2) suy ra: $\Rightarrow \widehat{D_1}=\widehat{F_1}$

   Mà hai góc này ở vị trí đồng vị

   ⇒ DE // BF (đpcm)

   b) Xét tứ giác DEBF có:

   DE // BF (chứng minh ở câu a)

   BE // DF (vì AB // CD)

   ⇒ DEBF là hình bình hành.

   Bài 46 trang 92 Toán 8 Tập 1:Các câu sau đúng hay sai?

   a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

   b) Hình thang có hai cạnh bên song song là hình bình hành

   c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

   d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

   Lời giải

   a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

   b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

   c) Sai.

   Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.

   

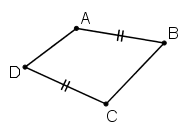
   d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

   

   Bài 47 trang 93 Toán 8 Tập 1: Cho hình 72. Trong đó ABCD là hình bình hành

   a) Chứng minh rằng AHCK là hình bình hành

   b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

   Lời giải

   

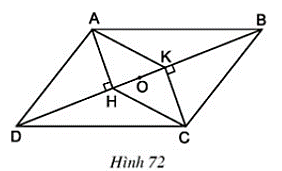
   a) Vì ABCD là hình bình hành

   ⇒ AD // BC và AD = BC.

   $\Rightarrow \widehat{ADH}=\widehat{ABK}$(hai góc so le trong)

   Xét $\Delta AHD$ và $\Delta CKB$, có:

   $\widehat{AHD}=\widehat{CKB}={90}^0$

   AD = BC (cmt)

   $\widehat{ADH}=\widehat{ABK}$(cmt)

   ⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)

   ⇒ AH = CK

   Ta có: AH ⊥ BD; CK ⊥ BD ⇒ AH // CK

   Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.

   b) Hình bình hành AHCK có O là trung điểm HK nên O là trung điểm của AC

   ⇒ A, C, O thẳng hàng.

   Bài 48 trang 93 Toán 8 Tập 1: Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

   Lời giải:

   

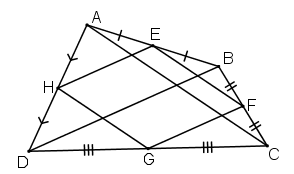
   +) Xét có:

   E là trung điểm AB

   F là trung điểm BC

   ⇒ EF là đường trung bình của tam giác ABC

   ⇒ EF // AC và $\text{EF}=\frac{AC}{2}$ (1)

   +) Xét $\Delta ADC$, có:

   H là trung điểm AD

   G là trung điểm CD

   ⇒ HG là đường trung bình của tam giác ACD

   ⇒ HG // AC và $HG=\frac{AC}{2}$ (2)

   Từ (1) và (2) suy ra : EF // HG (cùng // AC) và EF = HG (cùng bằng AC)

   ⇒ tứ giác EFGH là hình bình hành.

   Bài 49 trang 93 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

   a) AI // CK

   b) DM = MN = NB

   Lời giải:

   

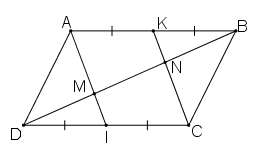
   a) Ta có: K là trung điểm của AB $\Rightarrow AK=\frac{AC}{2}$.

   Ta có: I là trung điểm của CD $\Rightarrow CI=\frac{CD}{2}$.

   Vì ABCD là hình bình hành

   ⇒ AB // CD hay AK // CI

   và AB = CD hay AK = CI

   Xét tứ giác AKCI có AK // CI và AK = CI

   ⇒ AKCI là hình bình hành.

   b) Vì AKCI là hình bình hành

   ⇒ AI//KC hay MI//NC.

   Xét ΔDNC có:

   I là trung điểm DC

   IM // NC

   ⇒ M là trung điểm DN

   ⇒ DM = MN (1)

   Xét ΔBAM có:

   K là trung điểm AB

   KN//AM

   ⇒ N là trung điểm BM

   ⇒ MN = NB (2)

   Từ (1) và (2) suy ra DM = MN = NB.
5. Dấu hiệu nhận biết hình bình hành chi tiết, đầy đủ năm 2023
   Hình bình hành là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nó là một dạng đặc biệt của hình thang.

   Trong không gian 3 chiều, khối tương đương với hình bình hành là hình khối lục diện.

   2. Tính chất hình bình hành

   Trong hình bình hành:

   – Các cạnh đối song song với nhau và bằng nhau.

   – Các góc đối bằng nhau.

   – Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

   3. Dấu hiệu nhận biết hình bình hành

   1/ Tứ giác có các cạnh đối song song là hình bình hành.

   Tứ giác ABCD có AB//CD và AD//CB thì ABCD là hình bình hành.

   2/ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

   Tứ giác ABCD có AB = CD, AD =BC thì ABCD là hình bình hành.

   3/ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

   Tứ giác ABCD có AB//CD và AB = CD hoặc AD//BC và AD = BC thì ABCD là hình bình hành.

   4/ Tứ giác có các góc đối bằng nhau là hình bình hành.

   Tứ giác ABCD có  thì ABCD là hình bình hành.

   5/ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

   Tứ giác ABCD có AC cắt BD tại O. Nếu OA = OC, OB = OD thì ABCD là hình bình hành.

   4. Diện tích hình bình hành

   Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình bình hành.

   Diện tích hình bình hành được tính theo công thức bằng tích của cạnh đáy nhân với chiều cao.

   S_ABCD = a.h

   Trong đó:

   + S là diện tích hình bình hành

   + a là cạnh đáy của hình bình hành

   + h là chiều cao nối tử đỉnh tới đáy của một hình bình hành.

   5. Chu vi hình bình hành

   Chu vi hình bình hành được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích, bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ. Nói cách khác, chu vi hình bình hành là tổng độ dài của 4 cạnh.

   Công thức cụ thể như sau:

   C = 2 x (a+b)

   Trong đó:

   + C là chu vi hình bình hành.

   + a và b là cặp cạnh kề nhau của hình bình hành.

   6. Ví dụ về hình bình hành

   Ví dụ 1: Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD

   a. Chứng minh: AF // CE

   b. Gọi M, N theo thứ tự là giao điểm của BD với AF, CE. Chứng minh: DM = MN = NB

   Hướng dẫn:

   

   a. Vì ABCD là hình bình hành:

   ⇒ AB = CD (tính chất)

   mà E thuộc AB và F thuộc DC ⇒ AE // FC

   Vì E, F là trung điểm của AB và CD

   ⇒ AE = EB = DF = FC

   Xét tứ giác AECF có:

   AE = FC và AE // FC

   ⇒ AECF là hình bình hành (DHNB) ⇒ AF // EC (tính chất)

   b. Gọi AC giao BD tại O

   Xét tam giác ADC có:

   DO, AF là trung tuyến (AO = OC, DF = FC)

   AF giao DO tại M

   ⇒ M là trọng tâm của tam giác ADC

   ⇒ DM = 2/3 DO = 2/3 BO (1)

   và OM = 1/3 DO = 1/3 BO (2) (do DO = BO)

   Xét tam giác ABC có:

   BO, CE là trung tuyến

   BO giao CE tại N

   ⇒ N là trọng tâm của tam giác ABC

   ⇒ BN = 2/3 BO (3)

   và ON = 1/3 BO (4)

   Từ (2), (4) ⇒ MN = OM + ON = 1/3 BO + 1/3 BO = 2/3 BO (5)

   Từ (1), (3) và (5) ⇒ DM = BN = MN

   Ví dụ 2: Hình bình hành ABCD, O là giao điểm của hai đường chéo, E và F theo thứ tự là trung điểm của OD và OB.

   a. Chứng minh: AE // CF

   b. Gọi AE giao CD tại K. Chứng minh: DK = 1/2 KC

   Hướng dẫn:

   

   a. AC giao BD tại O ⇒ OD = BO

   Vì E, F là trung điểm của DO và BO ⇒ DE = EO = OF = FB

   Xét tứ giác AFCE có:

   AC giao EF tại O

   OA = OC

   OE = OF

   ⇒ AFCE là hình bình hành (DHNB)

   ⇒ AE // CF (tính chất)

   b. Từ O kẻ OM // EK

   Xét tam giác DOM có:

   OM // EK

   và E là trung điểm của DO

   ⇒ K là tung điểm của DM ⇒ DK = KM (1)

   Xét tam giác CDK có:

   OM // AK 

   và O là trung điểm của AC

   ⇒ M là trung điểm của KC ⇒ CM = KM (2)

   Từ (1) và (2) ⇒ DK = KM = CM

   mà KM + CM = KC

   ⇒ DK = 1/2 KC

   Ví dụ 3:

   Cho hình bình hành có cạnh đáy bằng 12cm, cạnh bên bằng 7cm, chiều cao bằng 5cm. Hãy tính chu vi và diện tích của hình bình hành đó?

   Hướng dẫn:

   Chu vi của hình bình hành là:

   P = 2( 12 + 7) = 38 (cm)

   Diện tích hình bình hành là:

   S = a.h = 12.5 = 60 (cm2)

   Ví dụ 4: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .

   Hướng dẫn:

   

   Xét tứ giác BEDF có

   ⇒ BEDF là hình bình hành

   ⇒ BE = DF (hai cạnh đối song song và bằng nhau)

   Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ       ( 1 )

   BEDF là hình bình hành nên BEDˆ = DFBˆ       ( 2 )

   Mà

   Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ       ( 4 )

   Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 180⁰      (5)

   Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 180⁰      (5)

   Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)

   Ví dụ 5: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.

   a) Chứng minh AHCK là hình bình hành.

   b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.

   Hướng dẫn:

   

   a) Từ giả thiết ta có: ⇒ AH//CK.      ( 1 )

   Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:

    ⇒ Δ ADH = Δ CBK

   (trường hợp cạnh huyền – góc nhọn)

   ⇒ AH = CK (cạnh tương tứng bằng nhau)       ( 2 )

   Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.

   b) Áp dụng tính chất đường chéo của hình bình hành AHCK

   Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường

   Do O là trung điểm của HK nên O cũng là trung điểm của AC

   ⇒ A, O, C thẳng hàng.

   Ví dụ 6: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:

   a) AK//CI

   b) DM = MN = NB

   Hướng dẫn:

   

   a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:

   

   Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.

   b) Theo câu a, AICK là hình bình hành

   ⇒ AK//CI. Khi đó , ta có:

   Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:

   ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:

    ⇒ DM = MN = NB

   Ví dụ 7: Tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD.

   a. Chứng minh: EFGH là hình bình hành

   b. Cho AD = a, BC = b. Tính chu vi hình hình hành EFGH

   Hướng dẫn:

   

   a. Xét tam giác ABD có:

   F và E lần lượt là trung điểm của AB, BD ⇒ EF là đường trung bình của tam giác ABD

   ⇒ EF // AD (1)

   và EF = 1/2 AD (2)

   Tương tự, ta có GH là đường trung bình của tam giác ACD

   ⇒ GH // AD (3)

   và GH = 1/2 AD (4)

   Từ (1) và (3) ⇒ EF // GH

   (2) và (4) ⇒ EF = GH

   ⇒ tứ giác GHEF là hình bình hành

   b. Ta có: GH = EF = 1/2 AD = 1/2 a

   FG = HE = 1/2 BC = 1/2 b

   Chu vi hình binh hành GFEH là:

   C = (1/2 a + 1/2 b) .2 = a + b

   Ví dụ 8: Cho tam giác ABH, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. Chứng minh:

   a. BDCH là hình bình hành

   b. góc BAC + góc BDC = 180°

   c. H, M, D thẳng hàng (M là trung điểm BC)

   Hướng dẫn:

   

   a. Ta có: CH vuông góc AB

   và BD vuông góc AB 

   ⇒ CH // DB (1)

   Lại có: BH vuông góc AC

   và CD vuông góc AC

   ⇒ BH // CD (2)

   Từ (1) và (2) ⇒ BHCD là hình bình hành (DHNB)

   b. Tứ giác ABCD có:

   góc BAC + góc ABD + góc BDC + góc ACD = 360°

   ⇒ góc BAC + 90° + góc BDC + 90° = 360°

   ⇒ góc BAC + góc BDC = 180°

   c. Vì BHCD là hình bình hành nên BC cắt HD tại trung điểm của mỗi đường

   Ta có: M là tung điểm của BC

   ⇒ M là trung điểm của HD

   ⇒ H, M, D thẳng hàng

   Ví dụ 9: Hình bình hành ABCD. Lấy N thuộc AB, M thuộc CD sao cho AN = CM. Chứng minh:

   a. AM // CN

   b. DN = BM

   c. AC, BD, MN đồng quy

   Hướng dẫn:

   

   a. Xét tứ giác ABCD có:

   AN = CM

   AN // CM (do AB//CD)

   ⇒ ANCM là hình bình hành

   ⇒ AM // CN

   b. Ta có: BN = AB – AN

   DM = DC – CM

    mà AB = DC, AN = CM

   ⇒ BN = DM

   mà  BN // DM (do AB // CD)

   ⇒ BNDM là hình bình hành (DHNB)

   ⇒ DN = BM (tính chất)

   c. Gọi AC giao BD tại O (1)

   ⇒ O là trung điểm của AC và BD

   Ta có: ANCM là hình bình hành và O là trung điểm cua đường chéo Ac

   ⇒ O là trung điểm của MN

   ⇒ O thuộc MN (2)

   Từ (1) và (2) ⇒ AC, BD, MN đồng quy

   Ví dụ 10: Một mảnh đất hình bình hành có cạnh đáy là 47m, mở rộng mảnh dất bằng cách tăng cạnh đáy của hình bình hanh thêm 7m, thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Tính diện tích mảnh đất ban đầu?

   Hướng dẫn:

   Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.

   Chiều cao mảnh đất là: 189 ; 7 = 27m

   Diện tích mảnh đất hình bình hành ban đầu là: S = 27 . 47 = 1269 m2