Hình thoi là tứ giác có bốn cạnh bằng nhau, là hình bình hành đặc biệt với hai cạnh kề bằng và hai đường chéo vuông góc với nhau.
Trong hình thoi:
– Các góc đối nhau bằng nhau;
– Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;
– Hai đường chéo là các đường phân giác của các góc của hình thoi;
– Hình thoi có tất cả tính chất của hình bình hành.
2. Dấu hiệu nhận biết hình thoi
Để có thể giải các bài tập liên quan đến hình thoi cần nắm được Dấu hiệu nhận biết hình thoi như sau:
– Tứ giác có bốn cạnh bằng nhau;
– Hình bình hành có hai cạnh kề bằng nhau;
– Hình bình hành có hai đường chéo vuông góc nhau;
– Hình bình hành có một đường chéo là đường phân giác của một góc.
3. Công thức tính diện tích hình thoi
Dấu hiệu nhận biết hình thoi đã được giải đáp ở trên theo đó công thức tính diện tích hình thoi như sau: Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo.
S= ½ (d1 x d2)
4. Công thức tính chu vi hình thoi
Chu vi của hình thoi bằng độ dài một cạnh nhân với 4:
P = a x 4
5. Các cách để chứng minh tứ giác là hình thoi
Để chứng minh tứ giác là hình thoi cần nắm được Dấu hiệu nhận biết hình thoi và có thể áp dụng một trong số những cách chứng minh sau đây.
– Chứng minh tứ giác có 2 đường chéo là đường trung trực của nhau:
Ví dụ: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tư giác ABEC là hình thoi.
Theo bài ra, ta có:
ΔABC cân tại A có trung tuyến AM
=> AM đồng thời là đường trung trực của BC
=> Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau.
– Chứng minh tứ giác có bốn cạnh bằng nhau
Ví dụ: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
=> EH = 1/2 BD (1)
Chứng minh tương tự ta có: EF = ½ AC; FG = ½ BD; HG = ½ AC (2)
Vì ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3), ta suy ra EH = EF = HG = GF
=> Tứ giác EFGH là hình thoi do có bốn cạnh bằng nhau. (đ.p.c.m)
– Chứng minh tứ giác là hình bình hành có hai đường chéo vuông góc
Ví dụ: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong của các tam giác AOB; BOC; COD và DOA là đỉnh của một hình thoi.
Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét ΔBMO và ΔDPO có:
Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)
=> ΔBMO = ΔDPO (g. c. g)
=> OM = OP và các điểm M, O, P thẳng hàng (6)
Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (7)
Từ (6) và (7) Suy ra: Tứ giác MNPQ là hình bình hành do các đường chéo cắt nhau tại trung điểm mỗi đường. (8)
Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON. (9)
Từ (8) và (9) suy ra: MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc. (đ.p.c.m)
– Chứng minh tứ giác là hình bình hành có hai cạnh kề bằng nhau
Ví dụ: Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: IMNK là hình thoi.
Theo giả thiết ta có: M là trung điểm của BE và I là trung điểm của DE
=> MI là đường trung bình của ΔBDE
=> MI // BD và MI = 1/2 BD
Chứng minh tương tự, ta có:
NK // BD và NK= 1/2 BD
Do có MI // NK và MI = NK nên tứ giác MINK là hình bình hành (4)
Chứng minh tương tự, ta có: IN là đường trung bình của ΔCDE
=> IN = 1/2 CE mà CE = BD (gt) => IN = IM (5)
Từ (4) và (5) suy ra Tứ giác MINK là hình thoi do là hình bình hành có hai cạnh kề bằng nhau.
6. Bài tập liên quan đến hình thoi
Ví dụ 1 : Cho hình thoi ABCD có AB = BC = CD = DA = 5cm. Tính diện tích hình thoi.
Hướng dẫn giải:
Áp dụng công thức ta có chu vi hình thoi ABCD là:
P = 4.5 = 20(cm)
Ví dụ 2: Trong các hình sau, hình nào là hình thoi? Vì sao?
Hướng dẫn:
a) Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi
b) Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành.
Hình bình hành ABCD có đường chéo AC là đường phân giác góc nên ABCD là hình thoi.
c) Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi
d) Ta có: B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD (1)
A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD (2)
Từ (1) và (2) suy ra, AC = AD = BC = BD
Do đó, ABCD là hình thoi.
e) Tứ giác ABCD có các cạnh đối diện không bằng nhau, do đó ABCD không là hình thoi.
Ví dụ 3:
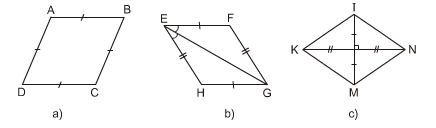
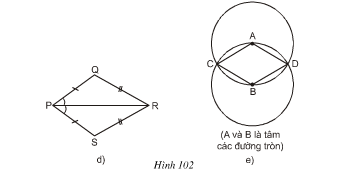
Tìm các hình thoi trên hình 102.
Lời giải:
Các tứ giác ở hình 102a, b, c, e là hình thoi.
– Hình 102a: ABCD là hình thoi (theo định nghĩa)
– Hình 102b: EFGH là hình thoi (theo dấu hiệu nhận biết 4)
– Hình 102c: KINM là hình thoi (theo dấu hiệu nhận biết 3)
– Hình 102e: ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.
Ví dụ 4: Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
A. 6cm; B. √41 cm ; c) √164cm ; d) 9cm
Lời giải:
Xét bài toán tổng quát:
ABCD là hình_thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
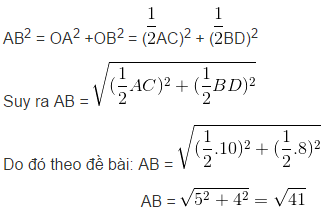
Vậy B đúng
Ví dụ 5:
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình_thoi.
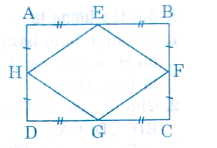
Lời giải:
Ta có: AE = BE = ½.AB
DG = GC = ½.DC
Mà AB = DC (ABCD là hình chữ nhật)
=> AE = BE = DG = GC.
Chứng minh tương tự ta có AH = HD = FB = FC
Xét ΔEAH và ΔGDH có:
AE = DG;
AH = HD
=> ΔEAH = ΔGDH => HE = HG.
Chứng minh tương tự ta có: EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
Ví dụ 6: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Lời giải:
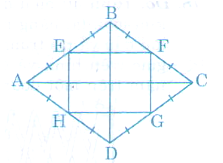
Ta có: EB = EA, FB = FA (gt)
Nên EF là đường trung bình của ΔABC.
Do đó EF // AC
HD = HA, GD = GC (gt) nên HG là đường trung bình của ΔADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FG (2)
Từ (1) và (2) ta được EFGH là hình bình hành
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên Hình bình hành EFGH có góc E = 90o nên là hình chữ nhật
Ví dụ 7: Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
Lời giải:
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.
Hình thoi cũng là một hình bình hành nên giao điểm của hai đường chéo hình thoi là tâm đối xứng của hình.
b)
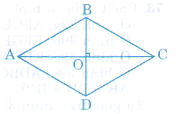
– BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
– Mọi điểm trên BD đều đối xứng qua chính đường thẳng BD. (*)
– Tâm O là tâm đối xứng mà O ∈ BD
=> BD là trục đối xứng của hình thoi. (**)
– Tương tự AC cũng là là trục đối xứng của hình thoi.
((*) Điểm đối xứng của điểm B qua BD chính là điểm B.
(**) Định nghĩa trục đối xứng: Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.)
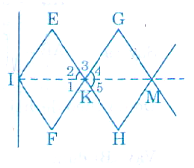
Ví dụ 8: Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bàng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hìnhthoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng ?
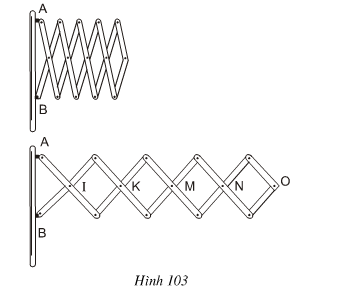
Lời giải:
Các tứ giác IEKF, KGMH là hình thoi nên KI là phân giác của góc EKF, KM là phân giác của góc GKH.
Suy ra I, K, M thẳng hàng.
Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.
Lưu ý: Để chứng minh 3 điểm thẳng hàng, ta có thể chứng minh tổng 3 góc kề nhau bằng 180o.
7. Một số lưu ý khi làm về bài tập hình thoi
Bài tập về hình thoi gồm những dạng bài tập như sau:
– Chứng minh một hình là hình thoi.
– Tính chu vi hình thoi.
– Tính diện tích hình thoi.
Những lưu ý khi làm bài tập về hình thoi cần biết đó là cần phải nắm vững các kiến thức về dấu hiệu, tính chất cũng như công thức tính chu vi và diện tích hình thoi. Từ đó có thể áp dụng vào việc giải các bài tập từ cơ bản đến nâng cao.
Khi nhận biết những dấu hiệu như thế nào là hình thoi thì việc chứng minh trong toán hình sẽ trở nên đơn giản và dễ dàng hơn.