Biết độ dài các cạnh của mỗi tam giác trong hình sau là bằng nhau, có tất cả bao nhiêu tam giác đều?

Câu hỏi:

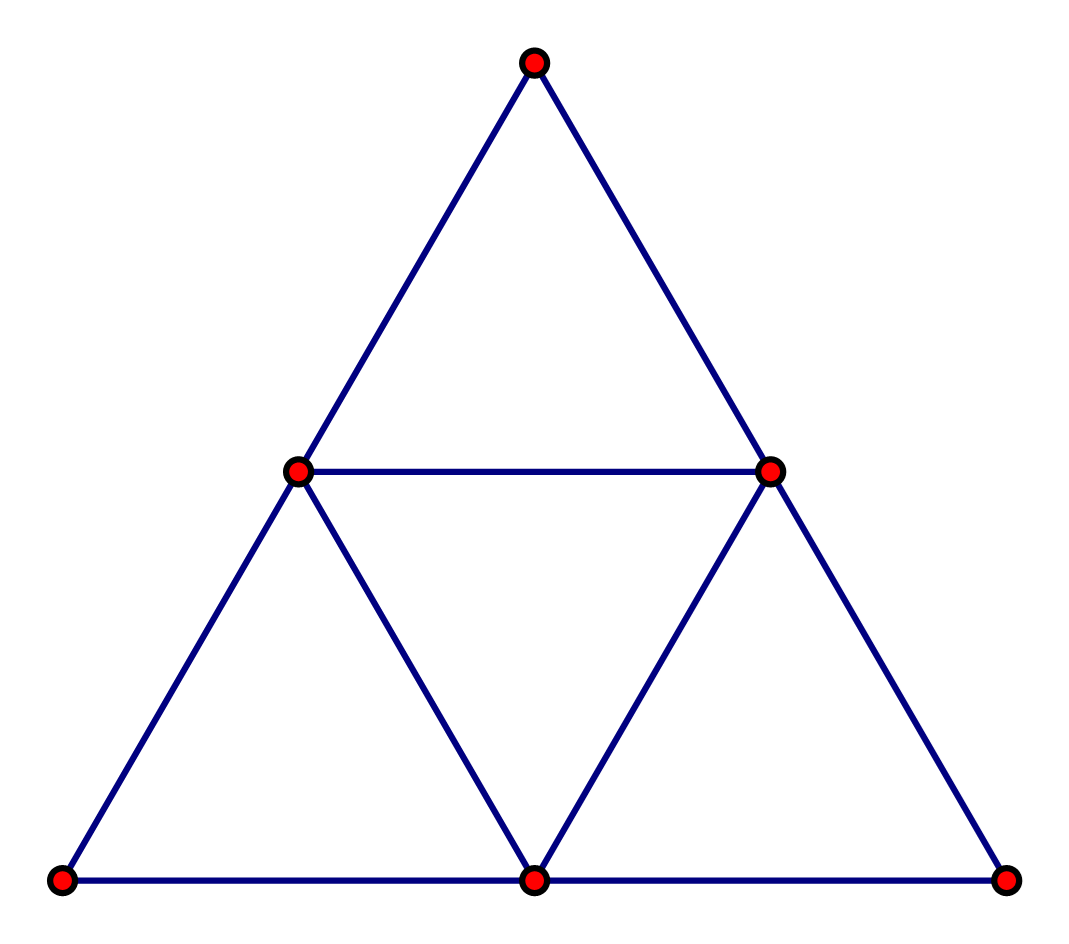
Biết độ dài các cạnh của mỗi tam giác trong hình sau là bằng nhau, có tất cả bao nhiêu tam giác đều?

A. 3;

B.  4;

C.  5;

Đáp án chính xác

D.  6.

Trả lời:

Hướng dẫn giải
Đáp án đúng là: C
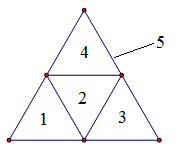
Quan sát hình ta đếm được 5 tam giác đều.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Hình vuông (mới 2023 + bài tập) – Toán 8
   Lý thuyết Hình vuông

   A. Lý thuyết

   1. Định nghĩa

   Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

   

   Tổng quát: ABCD là hình vuông ⇔

   Nhận xét:

   + Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

   + Hình vuông là hình thoi có bốn góc vuông.

   + Hình vuông vừa là hình chữ nhật vừa là hình thoi.

   2. Tính chất

   Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

   3. Dấu hiệu nhận biết hình vuông

   + Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

   + Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

   + Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

   + Hình thoi có một góc vuông là hình vuông.

   + Hình thoi có hai đường chéo bằng nhau là hình vuông.

   Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

   Hướng dẫn:

   

   + Xét tứ giác AEDF có Aˆ = Eˆ = Fˆ = 90⁰

   ⇒ AEDF là hình chữ nhật .       ( 1 )

   Theo giả thiết ta có AD là đường phân giác của góc Aˆ

   ⇒ EADˆ = DAFˆ = 45⁰.

   + Xét Δ AED có AEDˆ = 90⁰; DAEˆ = 45⁰ ⇒ EDAˆ = 45⁰

   ⇒ Δ AED vuông cân tại E nên AE = ED       ( 2 )

   Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)

   B. Bài tập tự luyện

   Bài 1: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.

   a) Chứng minh rằng BI ⊥ AK.

   b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.

   Hướng dẫn:

   

   Xét Δ BAI và Δ ADK có:

   ⇒ Δ BAI = Δ ADK ( c – g – c )

   ⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)

   Mà IAEˆ + EABˆ = 90⁰ ⇒ ABIˆ + EABˆ = 90⁰

   + Xét Δ ABE có EABˆ + ABEˆ + AEBˆ = 180⁰

   ⇒ AEBˆ = 180⁰ – ( ABEˆ + BAEˆ ) = 180⁰ – 90⁰ = 90⁰ hay AK ⊥ BI (đpcm)

   + Xét tứ giác EBCK có KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 360⁰

   ⇒ EBCˆ + EKCˆ = 180⁰.

   Mà AKDˆ + AKCˆ = 180⁰ nên EBCˆ = EKDˆ

   + Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ

   Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hay tam giác BEC cân tại C

   ⇒ CE = BC = AB (đpcm)

   Bài 2: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho MANˆ = 45⁰. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :

   a) Tính số đo KANˆ = ?

   b) Chu vi tam giác MCN theo a.

   Hướng dẫn:

   

   a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được

   

   ⇒ Δ ABM = Δ ADK ( c – g – c )

   Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:

    ⇒ KANˆ = A₃ˆ + A₄ˆ = A₁ˆ + A₃ˆ = 90⁰ – 45⁰ = 45⁰

   b) Đặt BM = DK = x thì KN = x + DN, MC = a – x, CN = a – DN

   Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

    ⇒ Δ AMN = Δ AKN ( c – g – c )

   ⇒ MN = KN (cạnh tương ứng bằng nhau)

   Khi đó, chu vi của tam giác MCN là

   MC + CN + MN = a – x + a – DN + x + DN = 2a.
2. Giáo án Hình vuông (2023) – Toán 8
   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Toán 8 Bài 12: Hình vuông

   A. Mục tiêu

   1. Kiến thức:

   – HS nắm được định nghĩa, tính chất, dấu hiệu nhận biết hình vuông, thấy được hình vuông là dạng đặc biệt của HCN và hình thoi.

   2. Kỹ năng:

   – HS biết cách vẽ hình vuông, biết chứng minh tứ giác là hình vuông.

   – HS biết cách vận dụng các kiến thức về hình vuông trong các bài toán chứng minh và trong các bài toán thực tế.

   3. Thái độ:

   – Tích cực, tự giác, hợp tác.

   4. Phát triển năng lực:

   – Biết cách vẽ hình: các đoạn thẳng bằng nhau, các đường vuông góc. Vận dụng tính chất để tính được các cạnh, các góc trong bài toán thực tế.

   B. Chuẩn bị

   1. Giáo viên:

   – Bảng phụ ghi dấu hiệu nhận biết 1 tứ giác là hình vuông, bảng phụ ghi ?2, thước thẳng.

   2. Học sinh:

   – Thước thẳng, ôn tập các kiến thức về HCN, hình thoi.

   C. Phương pháp

   – Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …

   D. Tiến trình dạy học

   1. Tổ chức lớp: Kiểm diện.

   2. Kiểm tra bài cũ:

   – HS 1: phát biểu định nghĩa và các tính chất HCN, vẽ HCN.

   – Câu hỏi tương tự với hình thoi.

   3. Bài mới

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động (5’)
   Treo bảng phụ, nêu câu hỏi. Gọi một HS lên bảng trả lời. – Gọi HS khác nhận xét – GV hoàn chỉnh và cho điểm – GV chốt lại bằng cách nhắc lại định nghĩa, tính chất và dấu hiệu nhận biết hình thoi (và hình chữ nhật)	HS lên bảng trả lời câu hỏi và làm bài ở bảng (cả lớp lắng nghe làm câu 3 vào vở) – HS nhận xét câu trả lời HS nghe để nhớ lại định nghĩa, tính chất, dấu hiệu nhận biết  hình chữ nhật, hình thoi	1- Định nghĩa hình thoi và các tính chất của hình thoi.  (4đ) 2- Nêu các dấu hiệu nhận biết về thoi (4đ) 3- Cho hình chữ nhật ABCD. Gọi E,F,G,H là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác EFGH là hình thoi
   Hoạt động 2: Hình thành kiến thức
   – GV vẽ hình vuông ABCD lên bảng và hỏi: – Tứ giác ABCD có gì đặc biệt? – Yêu cầu HS nên định nghĩa hình vuông. – GV chốt lại, nêu định nghiã và ghi bảng GV hỏi: – Định nghĩa hình chữ nhật và hình vuông giống nhau và khác nhau ở điểm nào? – Định nghĩa hình thoi và hình vuông giống và khác nhau ở điểm nào? – GV chốt lại và ghi bảng các định nghiã khác của hình vuông	– HS quan sát hình vẽ, trả lời – HS nêu định nghĩa hình vuông – Nhắc lại định nghiã, vẽ hình và ghi bài vào vở HS trả lời: – Giống: có bốn góc vuông    Khác: ở hình vuông có thêm đk bốn cạnh bằng nhau – Giống: bốn cạnh bằng nhau    Khác: ở hvuông có thêm đk có bốn góc vuông. – HS nhắc lại và ghi vào vở.	1) Định nghĩa: (SGK trang 107) Tứ giác ABCD là hình vuông  ⇔   A = B = C = D = 900 và AB = BC = CD = DA. *  Hình vuông là hình chữ nhật có bốn cạnh bằng nhau. * Hình vuông là hình thoi có bốn góc vuông. ⇒ Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
   Như vậy hình vuông có những tính chất gì? – Hãy kể ra các tính chất của hình vuông? – Từ đó em có thể nhận ra tính chất đặc trưng của đường chéo hình vuông là gì không? – GV chốt lại, ghi bảng tình chất hình vuông.	– HS suy nghĩ trả lời: có tất cả những tính chất của hình chữ nhật và hình thoi – HS kể các tính chất từ hình chữ nhật và hình thoi … – HS kết hợp tính chất về đường chéo của hai hình chữ nhật và hình thoi để suy ra … – HS nhắc lại và ghi bài	2) Tính chất:  – Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi  – Hai đường chéo của hình vuông thì bằng nhau và vuông góc với nhau tại trung điểm của mỗi đường. Mỗi đường chéo là một đường phân giác của các góc đối.
   – Đưa ra bảng phụ giới thiệu các dấu hiệu nhận biết một tứ giác là hình vuông. Hỏi: – Các câu trên đây đúng hay sai? Vì sao? – GV chốt lại và giải thích một vài dấu hiệu làm mẫu … – Qua các dấu hiệu nhận biết ta có  nhận xét gì? – Giới thiệu nhận xét – Treo bảng phụ hình vẽ 105. – Cho HS làm ?2	– HS ghi nhận các dấu hiệu nhận biết hình vuông vào vở – HS đọc (nhiều lần) từng dấu hiệu, suy nghĩ và trả lời… HS suy nghĩ trả lời… – HS ghi vào vở – HS quan sát hình vẽ và trả lời từng trường hợp (hình a,c,d)	3) Dấu hiệu nhận biết:  (SGKtrang 107) Nhận xét: Một tứ giác vừa là hình chữ nhật, vừa là hình thoi thì tứ giác đó là hình vuông.
   Hoạt động 3: Luyện tập (5’)
   Bài 80 trang 108 SGK – Treo bảng phụ ghi đề – Cho HS đứng tại chỗ trả lời – Cho HS khác nhận xét – GV hoàn chỉnh câu trả lời	– HS đọc đề bài – HS đứng tại chỗ trả lời – Giao điểm hai đường chéo của hình vuông là tâm đối xứng của nó – Hai đường trung trực của hai cạnh liên tiếp của hình vuông là hai trục đối xứng của nó – HS khác nhận xét – HS sửa bài vào vở	Bài 80 trang 108 SGK Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông
   4. VẬN DỤNG
   5. MỞ RỘNG
   Vẽ sơ đồ tư duy khái quát nội dung bài học Sưu tầm và làm một số bài tập nâng cao	Làm bài tập phần mở rộng.

   5.  Hướng dẫn học sinh tự học (3p)

   – Học theo SGK, chú ý các tính chất, dấu hiệu nhận biết hình vuông.

   – Làm các bài tập 79, 80, 82 (tr108-SBT).

   – HD 79: Sử dụng định lý pytago trong tam giác vuông.
3. Giải SGK Toán 8 Bài 12: Hình vuông
   Giải bài tập Toán lớp 8 Bài 12: Hình vuông

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 107 Toán 8 Tập 1: Đường chéo của hình vuông có những tính chất gì?

   Lời giải

   Hình vuông có tất cả các hình chữ nhật và hình thoi

   ⇒ Hai đường chéo của hình vuông có tính chất:

   Hai đường chéo bằng nhau

   Hai đường chéo cắt nhau tại trung điểm mỗi đường

   Hai đường chéo vuông góc với nhau.

   Câu hỏi 2 trang 108 Toán 8 Tập 1:Tìm các hình vuông trên hình 105.

   

   Lời giải

   Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm mỗi đường

   ⇒ ABCD là hình bình hành

   Hình bình hành ABCD có hai đường chéo AC = BD

   ⇒ ABCD là hình chữ nhật

   Hình chữ nhật ABCD có AB = BC

   ⇒ ABCD là hình vuông

   Xét tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm mỗi đường

   ⇒ MNPQ là hình bình hành

   Hình bình hành MNPQ có hai đường chéo MP = NQ

   ⇒ MNPQ là hình chữ nhật

   Hình chữ nhật MNPQ có MP ⊥ NQ tại O

   ⇒ MNPQ là hình vuông

   Xét tứ giác RSTU có 4 cạnh RS = ST = TU = RU

   ⇒ RSTU là hình thoi

   Hình thoi RSTU có một góc vuông

   ⇒ RSTU là hình vuông

   Bài tập (trang 108, 109)

   Bài 79 trang 108 Toán 8 Tập 1: a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, $\sqrt{18}$cm, 5cm hay 4cm?

   b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng:

   1dm, $\frac{3}{2}$dm, $\sqrt{2}$dm hay $\frac{4}{3}dm?$

   Lời giải:

   a)

   

   Gọi đường chéo của hình vuông có độ dài là a.

   Áp dụng định lí Pi-ta-go vào tam giác ADC, ta có:

   a² = 3² + 3² = 18

   Suy ra $a=\sqrt{18}$cm.

   Vậy đường chéo của hình vuông đó bằng $3\sqrt{2}$(cm).

   b)

   

   Gọi cạnh của hình vuông là a.

   Áp dụng định lí Pi-ta-go cho tam giác ADC, ta có:

   a² + a² = 2² 

   ⇒ 2a² = 4

   ⇒ a² = 2

   $\Rightarrow a=\sqrt{2}dm$

   Vậy cạnh của hình vuông đó bằng $\sqrt{2}$ (dm).

   Bài 80 trang 108 Toán 8 Tập 1: Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

   Lời giải:

   

   Gọi O là giao điểm của hai đường chéo

   + Hình vuông cũng là hình bình hành nên nhận O là tâm đối xứng của hình vuông ABCD.

   + Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.

   + Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.

   Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.

   Bài 81 trang 108 Toán 8 Tập 1:Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

   

   Lời giải:

   Ta có: $EA\perp AC,DF\perp AC\Rightarrow EA//DF$

   Ta lại có: $ED\perp AB,AF\perp AB\Rightarrow ED//AF$

   Xét tứ giác AEDF có:

   EA // DF (cùng vuông góc AF)

   DE // FA (cùng vuông góc AE)

   ⇒ AEDF là hình bình hành (theo định nghĩa)

   Hình bình hành AEDF có đường chéo AD là phân giác của góc $\widehat{BAC}$

   ⇒AEDF là hình thoi.

   Hình thoi AEDF có $\widehat{EAD}=90°$

   ⇒ AEDF là hình vuông.

   Bài 82 trang 108 Toán 8 Tập 1:Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

   

   Lời giải:

   Do ABCD là hình vuông nên AB = BC = CD = DA.

   Ta có: EB = AB – AE, CF = BC – BF,

   DG = DC – CG, AH = AD – DH

   Mà AE = BF = CG = DH (gt)

   và AB = BC = CD = DA (cmt)

   $\Rightarrow$ BE = CF = DG = HA

   Xét $\Delta AEH$ và $\Delta BFE$, có:

   $\widehat{EAH}=\widehat{FBE}=90°$

   AE = BF (gt)

   HA= BE (cmt)

   $\Rightarrow$ ΔAEH = ΔBFE (c – g – c)

   $\Rightarrow$ EH = FE (hai cạnh tương ứng) (1)

   Xét $\Delta CGF$ và $\Delta BFE$, có:

   $\widehat{GCF}=\widehat{FBE}=90°$

   CG = BF (gt)

   CF = BE (cmt)

   $\Rightarrow$ ΔCGF = ΔBFE (c – g – c)

   $\Rightarrow$ GF = FE (hai cạnh tương ứng) (2)

   Xét ΔCGF và ΔDHG, có:

   $\widehat{GCF}=\widehat{HDG}=90°$

   CG = DH (gt)

   CF = DG (cmt)

   $\Rightarrow$ ΔCGF = ΔDHG (c – g – c)

   $\Rightarrow$ GF = HG (hai cạnh tương ứng) (3)

   Từ (1), (2) và (3) suy ra: HE = EF = FG = GH.

   Suy ra tứ giác EFGH là hình thoi

   Vì ΔAEH = ΔBFE (cmt)

   $\Rightarrow \widehat{AHE}=\widehat{\text{BEF}}$ (2 góc tương ứng)

   Mà $\widehat{AHE}+\widehat{\text{AEH}}={90}^0$ (hai góc phụ nhau)

   $\Rightarrow \widehat{AEH}+\widehat{\text{BEF}}=90°$

   Ta lại có: $\widehat{AEH}+\widehat{\text{BEF}}+\widehat{\text{HEF}}=180°$

   $\widehat{\text{HEF}}=180°-\left(\widehat{AEH}+\widehat{\text{BEF}}\right)={180}^0-{90}^0={90}^0$

   Hình thoi EFGH có $\widehat{\text{HEF}}={90}^0$ nên EFGH là hình vuông.

   Bài 83 trang 109 Toán 8 Tập 1:Các câu sau đúng hay sai?

   a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

   b) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

   c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

   d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

   e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

   Lời giải:

   a) Tứ giác có hai đường chéo vuông góc với nhau chưa đủ dữ kiện để khẳng định tứ giác này là hình thoi. Do đó a) sai.

   b) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường nên tứ giác đó là hình bình hành.

   Mà hai đường chéo này lại vuông góc với nhau nên tứ giác này là hình thoi.

   Do đó b) đúng.

   c) “Hình thoi là tứ giác có tất cả các cạnh bằng nhau” là định nghĩa của hình thoi nên c) đúng.

   d) Hình chữ nhật luôn có hai đường chéo bằng nhau nên d) sai.

   e) “Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông” là dấu hiệu nhận biết hình vuông. Do đó e) đúng.

   Bài 84 trang 109 Toán 8 Tập 1:Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

   a) Tứ giác AEDF là hình gì? Vì sao?

   b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

   c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

   Lời giải:

   

   a) Xét tứ giác AEDF, có: DE // AF, DF // AE (gt)

   Suy ra AEDF là hình bình hành.

   b) Giả sử AEDF là hình thoi khi đó AD là tia phân giác của góc A.

   Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.

   c) Nếu ΔABC vuông tại A thì hình bình hành AEDF có $\widehat{EAF}={90}^0$ nên AEDF là hình chữ nhật.

   d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

   Bài 85 trang 109 Toán 8 Tập 1:Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

   a) Tứ giác ADFE là hình gì? Vì sao?

   b) Tứ giác EMFN là hình gì? Vì sao?

   Lời giải:

   

   a) Vì E là trung điểm của AB $\Rightarrow AE=EB=\frac{AB}{2}$

   Vì F là trung điểm của CD $\Rightarrow CF=DF=\frac{CD}{2}$

   Ta có: AB = CD = 2AD = 2BC

   ⇒ AE = EB = BC = CF = FD = DA.

   + Tứ giác ADFE có AE // DF, AE = DF

   ⇒ ADFE là hình bình hành.

   Hình bình hành ADFE có $\widehat{DAE}={90}^0$

   ⇒ ADFE là hình chữ nhật.

   Hình chữ nhật ADFE là hình chữ nhật có AE = AD

   ⇒ ADFE là hình vuông.

   b) Vì AEFD là hình vuông nên ta có:

   $\text{AF}\perp DE\Rightarrow \widehat{EMF}={90}^0$(hai đường chéo vuông góc)

   $\widehat{AED}=\widehat{FED}=\frac{\widehat{AEF}}{2}=\frac{{90}^0}{2}={45}^0$(ED là phân giác của $\widehat{AEF}$)

   $ME=MF=\frac{DE}{2}=\frac{FA}{2}$

   Tứ giác EBCF có EB // CF, EB = CF nên EBCF là hình bình hành

   Hình bình hành EBCF có $\widehat{EBC}={90}^0$

   ⇒ EBCF là hình chữ nhật.

   Hình chữ nhật EBCF là hình chữ nhật có BE = BC

   ⇒ EBCF là hình vuông.

   $CE\perp BF\Rightarrow \widehat{ENF}={90}^0$ (hai đường chéo vuông góc)

   $\widehat{FEC}=\widehat{BEC}=\frac{\widehat{\text{BEF}}}{2}=\frac{{90}^0}{2}={45}^0$(EC là phân giác của )

   Ta có: $\widehat{MEN}=\widehat{\text{MEF}}+\widehat{\text{NEF}}={45}^0+{45}^0={90}^o$

   Xét tứ giác MENF có: $\widehat{MEN}=\widehat{\text{EMF}}=\widehat{\text{ENF}}={90}^o$

   Suy ra MENF là hình chữ nhật

   Lại có ME = MF nên EMFN là hình vuông.

   Bài 86 trang 109 Toán 8 Tập 1: Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì?

   

   Lời giải:

   – Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.

   – Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.
4. Dấu hiệu nhận biết hình vuông chi tiết, đầy đủ 2023
   Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

   

   Tổng quát: ABCD là hình vuông ⇔

   Nhận xét:

   + Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

   + Hình vuông là hình thoi có bốn góc vuông.

   + Hình vuông vừa là hình chữ nhật vừa là hình thoi.

   2. Tính chất

   Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

   3. Dấu hiệu nhận biết hình vuông

   + Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

   + Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

   + Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.

   + Hình thoi có một góc vuông là hình vuông.

   + Hình thoi có hai đường chéo bằng nhau là hình vuông.

   4. Công thức tính chu vi hình vuông

   Chu vi là độ dài đường bao quanh một hình hai chiều.

   

   Chu vi hình vuông là tổng độ dài của bốn cạnh của hình vuông đó; hoặc chu vi hình vuông bằng 4 lần độ dài của một cạnh hình vuông.

   Công thức tính chu vi hình vuông:

   P = a x 4

   Trong đó: 

   • P: Chu vi

   • a: độ dài một cạnh bất kỳ

   Ví dụ: Tính chu vi hình vuông có cạnh 4cm.

   Đáp án:

   Chu vi hình vuông là: P = 4 . 4 = 16 cm2

   5. Công thức tính diện tích hình vuông

   Diện tích hình vuông được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình vuông. 

   Diện tích hình vuông bằng bình phương chiều dài cạnh hình vuông.

   Công thức tính diện tích hình vuông:

   S = a x a = a2

   Trong đó:

   • S: diện tích 

   • a: chiều dài các cạnh hình vuông

   6. Bài tập liên quan đến hình vuông

   Ví dụ 1: Cho hình bên, tứ giác AEDF là hình gì? Vì sao?

   

   Đáp án:

   Tứ giác AEDF là hình vuông, vì:

   Theo hình vẽ, góc A = góc E = góc F = 90°

   Tứ giác có ba góc vuông nên nó là hình chữ nhật (DHNB).

   Xét hình chữ nhật AEDF có AD là đường phân giác của góc A (góc FAE = góc EAD = 45°)

   ⇒ AEDF là hình vuống (DHNB)

   Ví dụ 2: Hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

   a. ADFE là hình gì?

   b. MENF là hình gì?

   Đáp án:

   

   a. Gọi AD = a thì AB = 2a

   Vì E là trung điểm của AB, F là trung điểm của DC

   mà AB = DC, AB = 2AD

   ⇒ AE = EB = BC = CF = FD = AD = BC = EF = a

   Xét tứ giác ADFE có 4 cạnh bằng nhau là AD = DF = EF = AE = a 

   ⇒ ADFE là hình thoi

   Xét hình thoi ADFE có góc DAE = 90°

   ⇒ ADFE là hình vuông (DHNB)

   b. Tương tự như câu a, ta cũng chứng minh được tứ giác EBCF là hình vuông.

   Vì hình vuông AEFD và hình vuông EFCB đều có cạnh là a ⇒ Hai hình vuông này bằng nhau.

   Áp dụng tính chất về đường chéo vào hai hình vuông ADFE và MENF, ta được:

   AF vuông góc với DE, EC vuông góc với FB ⇒ Góc EMF = góc ENF = 90°

   Ta có: góc DEF + góc EDF = 90°

   góc FCE + góc CEF = 90°

   mà góc EDF = góc ECF (tính chất đường chéo trong hình vuông)

   ⇒ góc DEF + góc CEF = 90° hay góc MEN = 90°

   Xét tứ giác MFNE có góc MEN = góc ENF = góc EMF = 90°

   ⇒ MFNE là hình chữ nhật (DHNB)

   Lại có EF là đường phân giác của góc MEN (vì, góc DEF = góc FEC = 45°)

   ⇒ từ giác MFNE là hình vuông (DHNB)

   Ví dụ 3: Hình vuông ABCD. Trên BC lấy M, trên CD lấy N sao cho BM = CN và AM vuông góc BN

   Đáp án:

   

   Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta có:

   AB = BC

   góc A = góc B = 90

   BM = CN

   ⇒ tam giác ABM = tam giác BCN (cgc) nên AM = BN

   Gọi AM giao BN tại I

   – Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau, ta có:

   góc BAM + góc AMB = 90°

   góc BAM = góc NBC 

   ⇒ góc AMB + góc NBC = 90° (1)

   Áp dụng tính chất về góc vào tam giác BIM ta có:

   góc IBM + góc BIM + góc IMB = 180° (2)

   Từ (1) và (2) ⇒ góc BIM = 180° – 90° = 90° hay AM vuông góc BN

   Ví dụ 4: Hình vuông ABCD. Trên BC lấy M, qua A kẻ AN vuông góc AM (N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh:

   a. AM = AN

   b. B, I, D thẳng hàng

   Đáp án:

   

   a. Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:

   góc DAB = góc ABC = góc CDA

   góc A1 + góc A2 = góc A2 + góc A3 = góc DAB = 90° => góc A1 = góc A3

   AB = AD

   – Xét tam giác ABM và tam giác ADN có

   góc B = góc D = 90°

   AB = AD

   góc A1 = góc A3

   => tam giác ABM = tam giác ADN (gcg)

   => AM = AN

   b. Nối IA, IC thì IA và IC lần lượt là các đường trung tuyến ứng với cnahj huyền của hai tam giác vuông AMN, CMN.

   Áp dụng tính chất đường trung tuyến với cạnh dhueenf vào hai tam giác vuông trên và định nghĩa hình vông ta được:

   IA = IC = 1/2 MN

   BA = BC

   Điều nàu chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC.

   Mặt khác theo tính chất về đường chéo của hình vuông thì BD là trung trực của AC mà đoạn AC thì chỉ có một đường trung trực nên BI trùng với BD hay B, I, D thẳng hàng. 

   Ví dụ 5: Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F

   a. AEDF là hình gì?

   b. Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

   c. Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

   Đáp án:

   a. Tứ giác AEDF là hình bình hành

   Giải thích: Từ giả thiết: DE//AC và DF // AB

   ⇒ DE // AF và DF // AE

   Tứ giác AEDF có các cạnh đối song song nên nó là hình bình hành

   b. Giả sử AEDF là hình thoi khi đó theo tính chất vẽ đường chéo của hình thoi thì AD là đường phân giác của góc A.

   Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì tứ giác AEDF là hình thoi

   c. Nếu tam giác ABC vuông tại A thì hình bình hành AEDF là hình chữ nhật. Nếu tam giác ABC vuông tại A và D là giao điểm của tia phân giác góc A với BC thì AEDF vừa là chữ nhật vừa là hình thoi nên nó là hình vuông.

   Ví dụ 6: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.

   a) Chứng minh rằng BI ⊥ AK.

   b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.

   Đáp án:

   

   Xét Δ BAI và Δ ADK có:

   ⇒ Δ BAI = Δ ADK ( c – g – c )

   ⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)

   Mà IAEˆ + EABˆ = 90⁰ ⇒ ABIˆ + EABˆ = 90⁰

   + Xét Δ ABE có EABˆ + ABEˆ + AEBˆ = 180⁰

   ⇒ AEBˆ = 180⁰ – ( ABEˆ + BAEˆ ) = 180⁰ – 90⁰ = 90⁰ hay AK ⊥ BI (đpcm)

   + Xét tứ giác EBCK có KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 360⁰

   ⇒ EBCˆ + EKCˆ = 180⁰.

   Mà AKDˆ + AKCˆ = 180⁰ nên EBCˆ = EKDˆ

   + Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ

   Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hay tam giác BEC cân tại C

   ⇒ CE = BC = AB (đpcm)

   Ví dụ 7: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho MANˆ = 45⁰. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :

   a) Tính số đo KANˆ = ?

   b) Chu vi tam giác MCN theo a.

   Đáp án:

   

   a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được

   

   ⇒ Δ ABM = Δ ADK ( c – g – c )

   Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:

    ⇒ KANˆ = A₃ˆ + A₄ˆ = A₁ˆ + A₃ˆ = 90⁰ – 45⁰ = 45⁰

   b) Đặt BM = DK = x thì KN = x + DN, MC = a – x, CN = a – DN

   Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:

    ⇒ Δ AMN = Δ AKN ( c – g – c )

   ⇒ MN = KN (cạnh tương ứng bằng nhau)

   Khi đó, chu vi của tam giác MCN là

   MC + CN + MN = a – x + a – DN + x + DN = 2a.
5. Trong các tam giác dưới đây, tam giác nào là hình tam giác đều?
   
   

   Câu hỏi:
   

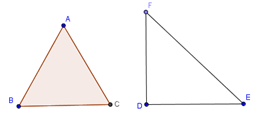
   Trong các tam giác dưới đây, tam giác nào là hình tam giác đều?
   

   Trả lời:

   Hướng dẫn giải:
   Ta thấy cạnh AB = AC = BC. Do đó tam giác ABC là tam giác đều.
   Ta thấy góc FDE = 90° ≠ 60°. Do đó tam giác FDE không có 3 góc bằng nhau và bằng 60°. Vậy tam giác FDE không là tam giác đều.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====