Bài 3 trang 78 sách bài tập Toán lớp 6 Tập 2: Dưới đây là hình ảnh một số di tích ở Hà Nội. Em hãy tìm tính đối xứng và cho biết tên các di tích này.

Câu hỏi:

Bài 3 trang 78 sách bài tập Toán lớp 6 Tập 2: Dưới đây là hình ảnh một số di tích ở Hà Nội. Em hãy tìm tính đối xứng và cho biết tên các di tích này.

Trả lời:

Lời giải:
Cả hai hình đều có trục đối xứng và không có tâm đối xứng được biểu diễn như trên hình vẽ:
Hình a)

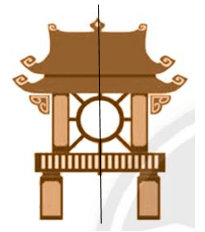
Hình b)

Hình a) là Khuê Văn Các, Hà Nội.
Hình b) là Nhà hát lớn Hà Nội.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giải SGK Toán 7 (Cánh diều): Bài tập cuối chương 7
   Giải bài tập Toán lớp 7 Bài tập cuối chương 7

   Giải Toán 7 trang 119 Tập 2

   Bài 1 trang 119 Toán 7 Tập 2: Cho tam giác ABC có: $\widehat{A}=42°,\widehat{B}=37°.$

   a) Tính $\widehat{C}$.

   b) So sánh độ dài các cạnh AB, BC, CA.

   Lời giải:

    

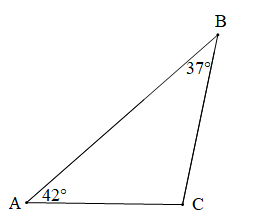
   a) Xét tam giác ABC: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc trong một tam giác)

   Suy ra $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-42°-37°=101°$.

   Vậy $\widehat{C}=101°.$ 

   b) Ta có: 37° < 42° < 101° nên $\widehat{B}<\widehat{A}<\widehat{C}$.

   Do đó CA < BC < AB (quan hệ giữa góc và cạnh đối diện)

   Vậy CA < BC < AB.

   Bài 2 trang 119 Toán 7 Tập 2: Tìm các số đo x, y trong Hình 140.

    

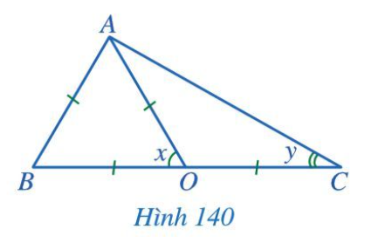
   Lời giải:

   Xét tam giác ABO có OA = AB = BO nên tam giác ABO đều.

   Do đó x = 60°.

   Tam giác OAC có OA = OC nên tam giác OAC cân tại O.

   Do đó $y=\widehat{OAC}=\widehat{OAC}$.

   Ta có $\widehat{AOB}$ là góc ngoài tại đỉnh O của $∆$OAC nên $\widehat{AOB}=\widehat{OCA}+\widehat{OAC}$.

   hay x = y + y = 2y.

   Suy ra 2y = 60°

   Do đó y = 30°.

   Vậy x = 60° và y = 30°.

   Bài 3 trang 119 Toán 7 Tập 2: Bạn Hoa đánh dấu ba vị trí A, B, C trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí A và B. Đường thứ nhất đi từ A đến C và đi tiếp từ C đến B, đường thứ hai đi từ B đến A (Hình 141). Theo em, đường nào đi dài hơn? Vì sao?

     

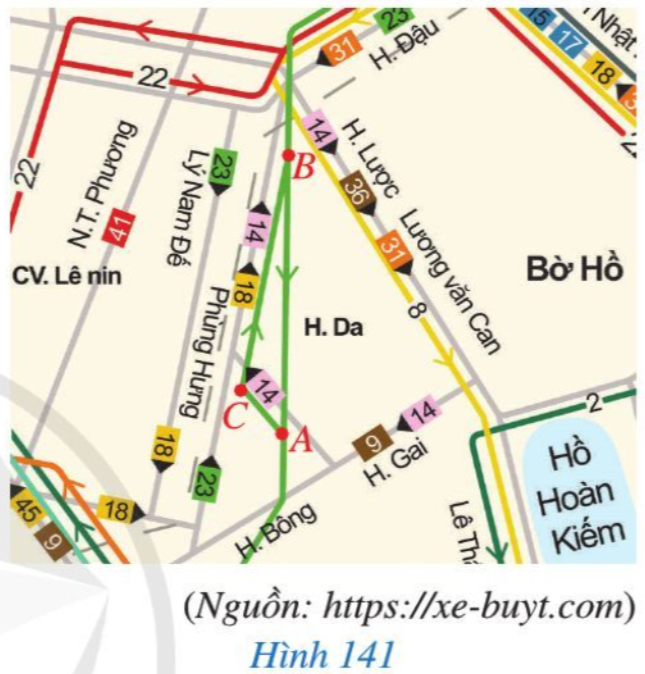
   Lời giải:

   Ba vị trí A, B, C mà bạn Hoa đánh dấu tạo thành ba đỉnh của tam giác ABC (Hình 141).

   Khi đó trong tam giác ABC ta có: AC + CB > BA (Bất đẳng thức tam giác)

   Vậy đường thứ nhất dài hơn đường thứ hai.

   Bài 4 trang 119 Toán 7 Tập 2: Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh: AI = MK.

   Lời giải:

   GT	$∆$ABC, $∆$MNP, AB = MN, BC = NP, CA = PM, I và K lần lượt là trung điểm của BC và NP.
   KL	AI = MK.

   Chứng minh (Hình vẽ dưới đây):

    

    

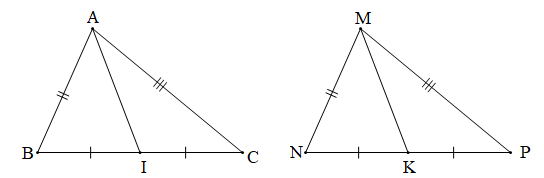
   Xét $∆$ABC và $∆$MNP có:

   AB = MN (giả thiết).

   BC = NP (giả thiết).

   CA = PM (giả thiết).

   Do đó $∆$ABC = $∆$MNP  (c.c.c).

   Suy ra $\widehat{ABC}=\widehat{MNP}$.

   Do I, K lần lượt là trung điểm của BC và NP nên $BI=IC=\frac{1}{2}BC$ và $NK=KP=\frac{1}{2}NP$ 

   Mà BC = NP (giả thiết) nên BI = NK.

   Xét $∆$ABI và $∆$MNK có:

   AB = MN (giả thiết).

   $\widehat{ABI}=\widehat{MNK}$ (chứng minh trên).

   BO = NK (chứng minh trên).

   Do đó $∆$ABI = $∆$MNK (c.g.c).

   Suy ra AI = MK (hai cạnh tương ứng).

   Vậy AI = MK.

   Bài 5 trang 119 Toán 7 Tập 2: Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N.

    

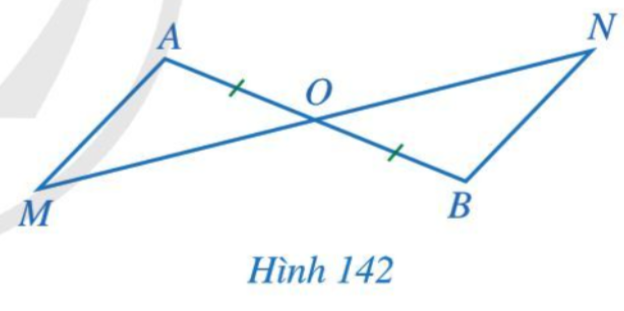
   Chứng minh:

   a) Nếu OM = ON thì AM // BN;

   b) Nếu AM // BN thì OM = ON.

   Lời giải:

   a)

   GT	$∆$OAM, $∆$OBN, O là trung điểm của AB, O nằm giữa hai điểm M, N. OM = ON
   KL	AM // BN;

   Chứng minh (Hình 142):

   Xét $∆$OAM và $∆$OBN có:

   AO = BO (do M là trung điểm của AB),

   $\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh),

   OM = ON (giả thiết).

   Do đó $∆$OAM = $∆$OBN (c.g.c).

   Suy ra $\widehat{AM\text{O}}=\widehat{BNO}$ (hai góc tương ứng)

   Mà hai góc này ở vị trí so le trong nên AM // BN (dấu hiệu nhận biết)

   Vậy AM //BN.

   b)

   GT	$∆$OAM, $∆$OBN, O là trung điểm của AB, O nằm giữa hai điểm M, N.   AM // BN
   KL	OM = ON.

   Chứng minh (Hình 142):

   Do AM // BN (giả thiết) nên $\widehat{MAO}=\widehat{NBO}$ (hai góc so le trong).

   Xét $∆$OAM và $∆$OBN có:

   $\widehat{MAO}=\widehat{NBO}$ (chứng minh trên),

   AO = BO (do M là trung điểm của AB),

   $\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh).

   Do đó $∆$OAM = $∆$OBN (g.c.g).

   Suy ra OM = ON (hai cạnh tương ứng).

   Vậy OM = ON.

   Bài 6 trang 119 Toán 7 Tập 2: Cho tam giác ABC cân tại A có

   $\widehat{ABC}=70°$. Hai đường cao BD và CE cắt nhau tại H.

   a) Tính số đo các góc còn lại của tam giác ABC.

   b) Chứng minh BD = CE.

   c) Chứng minh tia AH là tia phân giác của góc BAC.

   Lời giải:

   GT	$∆$ABC cân tại A, $\widehat{ABC}=70°$ BD $\perp$AC, CE $\perp$ AB, BD cắt CE tại H.
   KL	a) Tính số đo các góc còn lại của tam giác ABC; b) BD = CE; c) AH là tia phân giác của góc BAC.

   Chứng minh (Hình vẽ dưới đây):

    

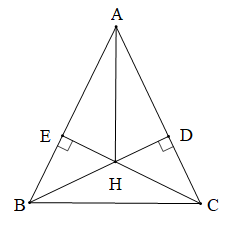
   a) Do tam giác ABC cân tại A (giả thiết)

   Nên AB = AC và $\widehat{ABC}=\widehat{ACB}=70°$ (tính chất tam giác cân)

   Xét tam giác ABC có $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc trong tam giác)

   Suy ra $\widehat{BAC}=180°-\widehat{ABC}-\widehat{ACB}=180°-70°-70°=40°$.

   Vậy $\widehat{ACB}=70°$ và $\widehat{BAC}=40°.$ 

   b) Xét $∆$ADB (vuông tại D) và $∆$ACE (vuông tại E) có:

   AB = AC (chứng minh trên),

   $\widehat{A}$ là góc chung,

   Do đó $∆$ABD = $∆$ACE (cạnh huyền – góc nhọn).

   Suy ra BD = CE (hai cạnh tương ứng).

   Vậy BD = CE.

   c) Vì $∆$ABD = $∆$ACE (chứng minh câu a) nên AD = AE (hai cạnh tương ứng).

   Xét $∆$AHE (vuông tại E) và $∆$AHD (vuông tại D) có:

   AE = AD (chứng minh trên),

   AH là cạnh chung.

   Do đó $∆$AHE  = $∆$AHD (cạnh huyền – cạnh góc vuông).

   Suy ra $\widehat{HA\text{E}}=\widehat{HA\text{D}}$ (hai góc tương ứng).

   Do đó AH là tia phân giác của $\widehat{EAD}$.

   Vậy AH là tia phân giác của $\widehat{BAC}$.

   Bài 7 trang 119 Toán 7 Tập 2: Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.

    

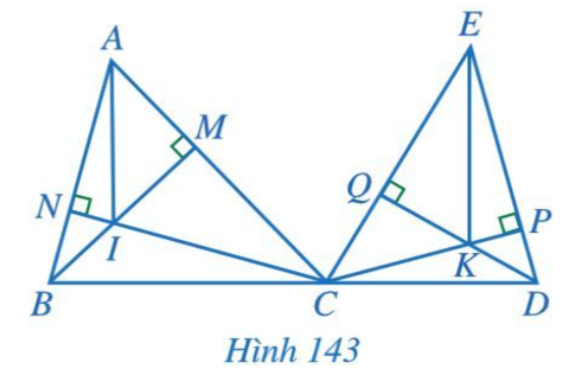
   Lời giải:

   GT	$∆$ABC nhọn và $∆$ECD nhọn Ba điểm B, C, D thẳng hàng, $∆$ABC: hai đường cao BM và CN cắt nhau tại I, $∆$ECD: hai đường cao CP và DQ cắt nhau tại K
   KL	AI // EK.

   Chứng minh (Hình 143):

   Vì $∆$ABC có hai đường cao BM và CN cắt nhau tại I (giả thiết) nên I là trực tâm của $∆$ABC.

   Suy ra AI $\perp$ BC.

   Vì $∆$ECD có hai đường cao CP và DQ cắt nhau tại K (giả thiết) nên K là trực tâm của $∆$ECD.

   Suy ra EK $\perp$ CD.

   Mà B, C, D thẳng hàng (giả thiết) nên

   • AI $\perp$ BC (chứng minh trên)  suy ra AI $\perp$ BD;

   • EK $\perp$ CD (chứng minh trên) suy ra EK $$ BD.

   Do đó AI // EK (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song)

   Vậy AI // EK.

   Giải Toán 7 trang 120 Tập 2

   Bài 8 trang 120 Toán 7 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144).

    

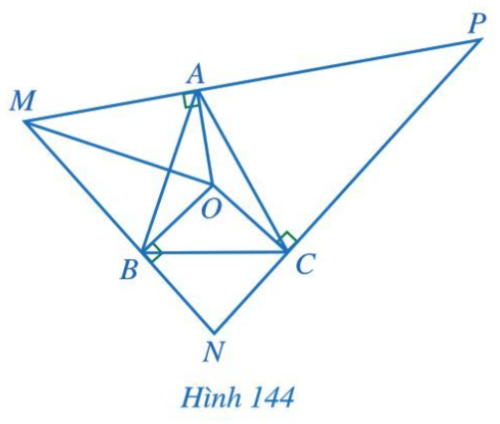
   Chứng minh:

   a) $∆$OMA = $∆$OMB và tia MO là tia phân giác của góc NMP;

   b) O là giao điểm ba đường phân giác của tam giác MNP.

   Lời giải:

   GT	$∆$ABC, O là giao điểm của ba đường trung trực, MP $\perp$ OA, MN $\perp$ OB, NP $\perp$ OC
   KL	a) $∆$OMA = $∆$OMB và tia MO là tia phân giác của $\widehat{NMP};$  b) O là giao điểm ba đường phân giác của tam giác MNP.

   Chứng minh (Hình 144):

   a) Vì O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.

   Xét $∆$OAM (vuông tại A) và $∆$OBM (vuông tại B) có:

   OM là cạnh chung,

   OA = OB (chứng minh trên),

   Do đó $∆$OAM = $∆$OBM (cạnh huyền – cạnh góc vuông).

   Suy ra $\widehat{OM\text{A}}=\widehat{OMB}$ (hai góc tương ứng).

   Khi đó MO là tia phân giác của $\widehat{BMA}$ hay MO là tia phân giác của $\widehat{NMP}$.

   Vậy tia MO là tia phân giác của $\widehat{NMP}$

   b) Nối OP (Hình vẽ dưới đây):

    

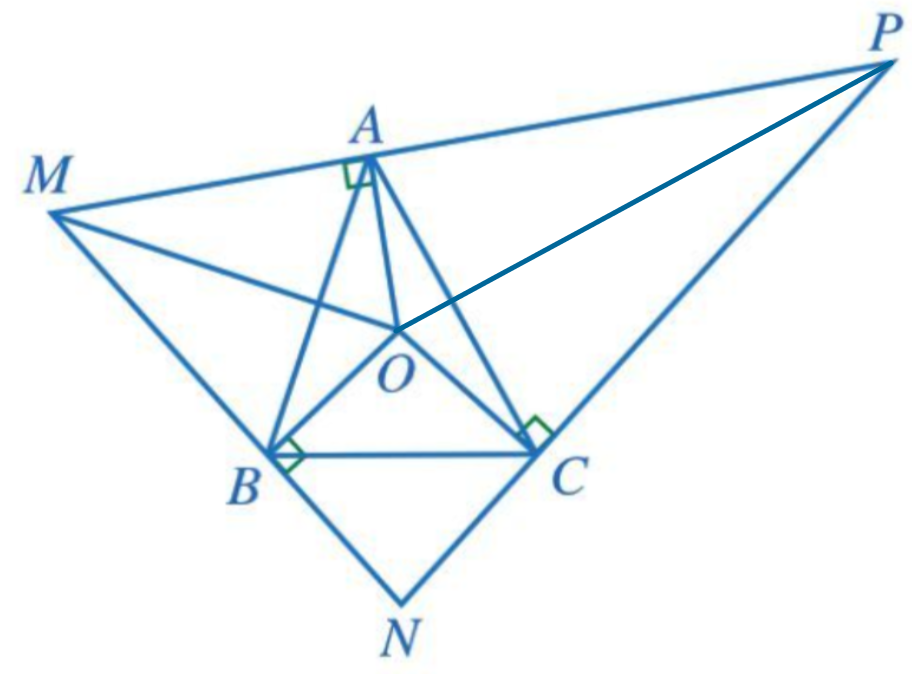
   Xét $∆$OAP (vuông tại A) và $∆$OCP (vuông tại C) có:

   OP là cạnh chung,

   OA = OC (chứng minh trên),

   Do đó $∆$OAP = $∆$OCP (cạnh huyền – cạnh góc vuông).

   Suy ra $\widehat{OP\text{A}}=\widehat{OPC}$ (hai góc tương ứng).

   Khi đó PO là tia phân giác của $\widehat{APC}$ hay PO là tia phân giác của $\widehat{MPN}$.

   Trong một tam giác, ba đường phân giác của tam giác đó luôn cùng đi qua một điểm

   Mà O là giao điểm hai đường phân giác của góc $\widehat{NMP}$ và góc $\widehat{MPN}$, do đó O là giao điểm ba đường phân giác của tam giác MNP.

   Vậy O là giao điểm ba đường phân giác của tam giác MNP.

   Bài 9 trang 120 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:

   a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.

   b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.

   Lời giải:

   a)

   GT	$∆$ABC cân tại A, G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt
   KL	Các điểm A, G, H, I, O cùng nằm trên một đường thẳng.

   Chứng minh (Hình vẽ dưới đây):

    

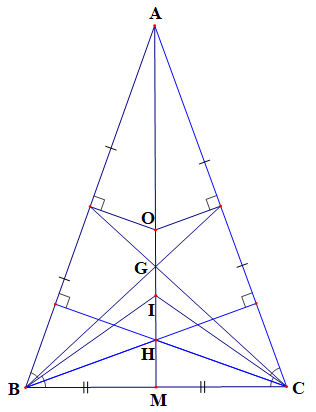
   +) Gọi M là trung điểm của BC.

   Khi đó AM là đường trung tuyến của $∆$ABC.

   Lại có G là trọng tâm của tam giác ABC (giả thiết) nên đường trung tuyến AM đi qua trọng tâm G của tam giác.

   Do đó A, G, M thẳng hàng (1).

   +) Vì M là trung điểm của BC nên MB = MC.

   Do tam giác ABC cân tại A (giả thiết) nên AB = AC và $\widehat{ABC}=\widehat{ACB}$.

   Xét $∆$AMB và $∆$AMC có:

   AK là cạnh chung,

   MB = MC (chứng minh trên),

   AB = AC (chứng minh trên),

   Do đó $∆$AMB = $∆$AMC (c.c.c).

   Suy ra $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng)

   Mà $\widehat{AMB}+\widehat{AMC}=180°$ (hai góc kề bù) nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

   Do đó AM $\perp$ BC hay AM là đường cao kẻ từ đỉnh A của tam giác ABC.

   Mặt khác H là trực tâm của tam giác ABC (giả thiết) nên đường cao AM đi qua trực tâm H của tam giác.

   Do đó A, H, M thẳng hàng (2).

   +) Vì O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.

   Xét $∆$OBM và $∆$OCM có:

   OK là cạnh chung,

   OB = OC (chứng minh trên),

   MB = MC (chứng minh trên),

   Do đó $∆$OBM = $∆$OCM (c.c.c).

   Suy ra $\widehat{OMB}=\widehat{OMC}$ (hai góc tương ứng)

   Mà $\widehat{OMB}+\widehat{OMC}=180°$ (hai góc kề bù) nên $\widehat{OMB}=\widehat{OMC}=\frac{180°}{2}=90°$.

   Do đó OK $\perp$ BC.

   Lại có AM $\perp$ BC (chứng minh trên)

   Suy ra A, O, M thẳng hàng (3).

   +) Do BI là tia phân giác của $\widehat{ABC}$ nên $\widehat{IBC}=\frac{1}{2}\widehat{ABC}$.

   Do CI là tia phân giác của $\widehat{ACB}$ nên $\widehat{ICB}=\frac{1}{2}\widehat{ACB}$.

   Mà $\widehat{ABC}=\widehat{ACB}$ (chứng minh trên) nên $\widehat{IBC}=\widehat{ICB}$ 

   Tam giác IBC có $\widehat{IBC}=\widehat{ICB}$ nên tam giác IBC cân tại I, do đó IB = IC.

   Xét $∆$IBM và $∆$ICM có:

   IB = IC (chứng minh trên),

   $\widehat{IBM}=\widehat{ICM}$ (do $\widehat{IBC}=\widehat{ICB}$),

   MB = MC (chứng minh trên),

   Do đó $∆$IBM = $∆$ICM (c.g.c).

   Suy ra $\widehat{IMB}=\widehat{IMC}$(hai góc tương ứng)

   Mà $\widehat{IKB}+\widehat{IKC}=180°$ (hai góc tương ứng) nên $\widehat{IMB}=\widehat{IMC}=\frac{180°}{2}=90°$.

   Do đó IM $\perp$ BC.

   Lại có AM $\perp$ BC (chứng minh trên)

   Suy ra A, I, K thẳng hàng (4).

   Từ (1), (2), (3) và (4) ta có A, G, H, I, O thẳng hàng.

   Vậy các điểm A, G, H, I, O thẳng hàng khi tam giác ABC cân tại A.

   b)

   GT	$∆$ABC, G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt, A, H, I cùng nằm trên một đường thẳng.
   KL	Tam giác ABC cân tại A.

   Chứng minh (Hình vẽ dưới đây):

    

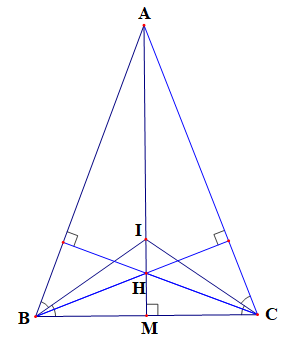
   Gọi M là chân đường cao kẻ từ A tới BC.

   Do đó AM là đường cao kẻ từ đỉnh A của tam giác ABC.

   Mà H là trực tâm của tam giác ABC (giả thiết) nên đường cao AM đi qua điểm H.

   Khi đó ba điểm A, H, M thẳng hàng.

   Mà A, H, I thẳng hàng (giả thiết) nên A, H, I, K thẳng hàng.

   Mà AI là tia phân giác của $\widehat{BAC}$ nên AM là đường phân giác của $\widehat{BAC}$.

   Do đó $\widehat{\text{MA}B}=\widehat{\text{MA}C}$.

   Xét $∆$ABM (vuông tại M) và $∆$ACM (vuông tại M) có:

   $\widehat{\text{MA}B}=\widehat{\text{MA}C}$ (chứng minh trên),

   AM là cạnh chung,

   Do đó $∆$ABM = $∆$ACM (cạnh góc vuông – góc nhọn kề).

   Suy ra AB = AC (hai cạnh tương ứng).

   Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

   Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.

   Bài 10 trang 120 Toán 7 Tập 2: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình.

    

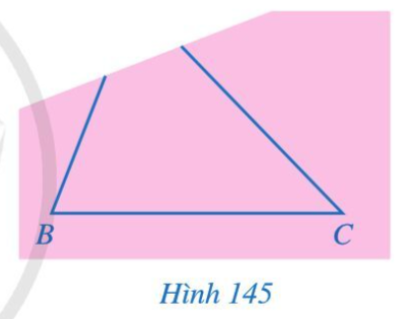
   Lời giải:

   Để tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất thì AD là nhỏ nhất.

   Khi đó theo tính chất đường xiên và đường vuông góc kẻ từ một điểm đến một đường thẳng, ta thấy DA nhỏ nhất khi AD là đường vuông góc kẻ từ D tới BC (tức là AD $\perp$ BC) hay D là chân đường vuông góc kẻ từ A đến BC.

   Ta xác định điểm D như sau:

   Bước 1. Kẻ hai đường cao xuất phát từ đỉnh B và đỉnh C của tam giác ABC.

   Bước 2. Gọi H là giao điểm của hai đường cao xuất phát từ đỉnh B và đỉnh C của tam giác ABC.

   Khi đó H chính là trực tâm của tam giác ABC.

   Suy ra đường cao AD của tam giác ABC đi qua điểm H.

   Do đó HD $\perp$ BC tại D.

   Bước 3. Từ H kẻ đường vuông góc với BC, cắt BC tại một điểm.

   Điểm này chính là điểm D cần tìm.

   Ta có hình vẽ sau:

    

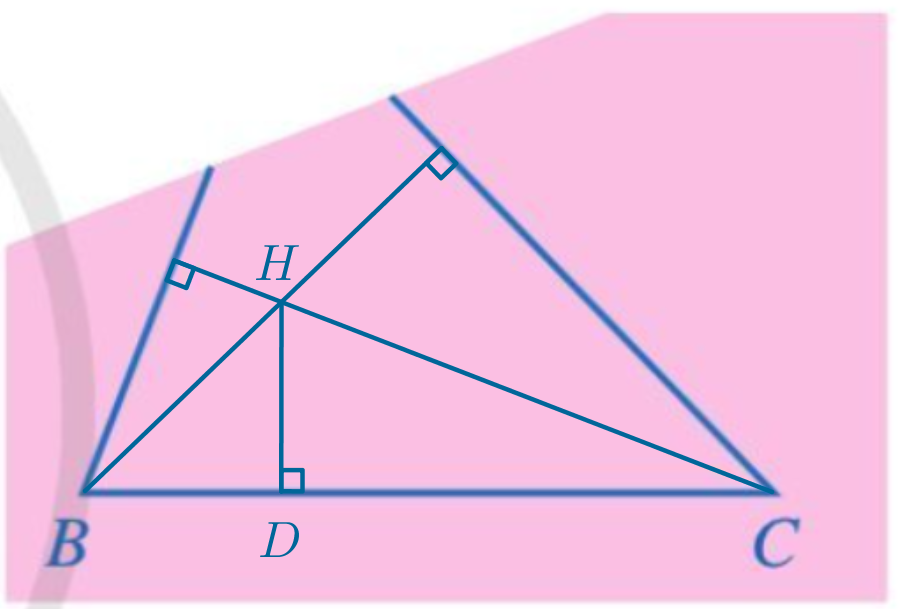
   Bài 11 trang 120 Toán 7 Tập 2: Cho tam giác MNP có $\widehat{M}=40°,\widehat{N}=70°.$ Khi đó $\widehat{P}$ bằng:

   A. 10°

   B. 55°;

   C. 70°;

   D. 110°.

   Lời giải:

   Đáp án đúng là: C.

   Trong tam giác MNP có: $\widehat{M}+\widehat{N}+\widehat{P}=180°$ (tổng ba góc trong một tam giác)

   $\widehat{P}=180°-\widehat{M}-\widehat{N}=180°-40°-70°=70°$.

   Vậy $\widehat{P}=70°.$ 

   Bài 12 trang 120 Toán 7 Tập 2: Cho tam giác nhọn MNP có trực tâm H. Khi đó, góc HMN bằng góc nào sau đây?

   A. Góc HPN.

   B. Góc NMP.

   C. Góc MPN.

   D. Góc NHP.

   Lời giải:

   Đáp án đúng là: A.

    

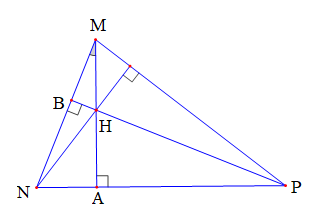
   Gọi A và B lần lượt là chân đường cao kẻ từ M và P của tam giác MNP.

   Xét tam giác MNA vuông tại A có $\widehat{ANM}+\widehat{AMN}=90°$ (trong tam giác vuông, tổng hai góc nhọn phụ nhau).

   Suy ra $\widehat{AMN}=90°-\widehat{ANM}$ hay $\widehat{HMN}=90°-\widehat{MNP}$  (1)

   Xét tam giác BNP vuông tại B có $\widehat{BNP}+\widehat{BPN}=90°$ (trong tam giác vuông, tổng hai góc nhọn phụ nhau)

   Suy ra $\widehat{BPN}=90°-\widehat{BNP}$  hay $\widehat{HPN}=90°-\widehat{MNP}$  (2)

   Từ (1) và (2) suy ra  $\widehat{HMN}=\widehat{HPN}$.

   Vậy $\widehat{HMN}=\widehat{HPN}.$

   Bài 13 trang 120 Toán 7 Tập 2: Cho tam giác MNP có MN = 1 dm, NP = 2 dm, MP = x dm với x ∈ {1; 2; 3; 4}. Khi đó, x nhận giá trị nào?

   A. 1.

   B. 2.

   C. 3.

   D. 4.

   Lời giải:

   Đáp án đúng là: B.

   Xét tam giác MNP ta có:

   NP – MN < MP < NP + MN (bất đẳng thức tam giác)

   Hay 2 – 1 < x < 2 + 1

   Do đó: 1 < x  < 3.

   Mà x $\in$ {1; 2; 3; 4} nên x = 2.

   Vậy x = 2.

   Bài 14 trang 120 Toán 7 Tập 2: Nếu tam giác MNP có trọng tâm G, đường trung tuyến MI thì tỉ số $\frac{MG}{MI}$ bằng

   A. $\frac{3}{4}$.

   B. $\frac{1}{2}$.

   C. $\frac{2}{3}$.

   D. $\frac{1}{3}$.

   Lời giải:

   Đáp án đúng là: C.

   Vì G là trọng tâm của tam giác MNP nên $\frac{MG}{MI}=\frac{2}{3}$.

   Vậy $\frac{MG}{MI}=\frac{2}{3}$

   Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

   Giải SGK Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

   Giải SGK Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

   Giải SGK Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

   Giải SGK Toán 7 Bài 13: Tính chất ba đường cao của tam giác

   Giải SGK Toán 7: Bài tập cuối chương 7
2. Giải SGK Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 7
   Giải bài tập Toán lớp 7 Bài tập cuối chương 7

   Giải Toán 7 trang 42 Tập 2

   Bài 1 trang 42 Toán lớp 7: Cho $A=x^{2}y+2xy-3y^2+4$. Tính giá trị của biểu thức A khi x = -2, y = 3.

   Phương pháp giải:

   Ta thay các x, y đề bài cho trước vào biểu thức rồi tính

   Lời giải:

   $A=x^{2}y+2xy-3y^2+4$

   Thay các x = -2 và y = 3 vào công thức ta có :

   $\begin{array}{l}A=(-2{)}^2.3+2(-2).3-{3.3}^2+4\\ =4.3-12-27+4\\ =-23\end{array}$

   Bài 2 trang 42 Toán lớp 7: Trong các biểu thức sau, biểu thức nào là đơn thức một biến ?

   a) 2y                                        b) 3x + 5

   c) 8                                           d)$21t^{12}$

   Phương pháp giải:

   Định nghĩa đa thức một biến.

   Lời giải:

   Các đa thức 1 biến là a, c, d

   Bài 3 trang 42 Toán lớp 7: Trong các biểu thức sau, biểu thức nào là đa thức một biến ?

   $3+6y$;                    $7x^2+2x-4x^4+1$;

   $\frac{2}{x+1}$;                                   $\frac{1}{3}x-5$.

   Phương pháp giải:

   – Dựa vào định nghĩa của đa thức 1 biến

   Lời giải:

   Các đa thức 1 biến là :

   $3+6y;7x^2+2x-4x^4+1;\frac{1}{3}x-5$ 

   Bài 4 trang 42 Toán lớp 7: Hãy viết một đa thức một biến bậc ba có 3 số hạng.

   Phương pháp giải:

   – Sử dụng các định nghĩa về bậc trong đa thức 1 biến

   Lời giải:

   $x^3+2x-1$

   Chú ý : Có nhiều cách khác nhau để viết đa thức nhưng trong bài này các số hạng trong đa thức luôn luôn là 3

   Bài 5 trang 42 Toán lớp 7: Hãy cho biết bậc của các đa thức sau:

   $A=3x-4x^2+1$

   $B=7$

   $M=x-7x^3+10x^4+2$ 

   Phương pháp giải:

   • Dựa vào các định nghĩa về bậc trong đa thức

   Lời giải:

   A có bậc là 2

   B có bậc là 0

   M có bậc là 4

   Bài 6 trang 42 Toán lớp 7: Cho đa thức P(x) = $x^3+27$. Tìm nghiệm của P(x) trong tập hợp $\left\{0;3;-3\right\}$

   Phương pháp giải:

   Ta xét P(x) = 0 rồi tìm x. Giá trị x tìm được là nghiệm của đa thức

   Lời giải:

   Xét P(x) = $x^3+27=0$

   $\begin{array}{l}\iff x^3=-27\\ \iff x^3=-27=(-3{)}^3\\ \Rightarrow x=-3\end{array}$

   Vì $-3\in \left\{0;3;-3\right\}$ nên -3 là 1 nghiệm 

   Bài 7 trang 42 Toán lớp 7: Tam giác trong Hình 1 có chu vi bằng (25y – 8) cm. Tìm cạnh chưa biết trong tam giác đó.

   

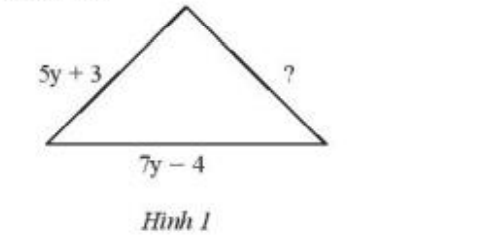
   Phương pháp giải:

   • Ta tính cạnh còn lại bằng cách lấy chu vi trừ đi 2 cạnh còn lại đã biết
   • Sử dụng qui tắc cộng trừ đa thức

   Lời giải:

   Theo đề bài ta có chu vi hình tam giác = 25y – 8 cm

   Ta có 2 cạnh của tam giác đã biết theo đề bài

   $\Rightarrow$ Cạnh còn lại cần tìm của tam giác là : 25y – 8 – 5y + 3 – 7y + 4 = 13y – 7 cm 

   Bài 8 trang 42 Toán lớp 7: Cho đa thức $M(x)=2x^4-5x^3+7x^2+3x$.

   Tìm các đa thức N(x), Q(x) sao cho:

   $N(x)-M(x)=-4x^4-2x^3+6x^2+7$

   và $M(x)+Q(x)=6x^5-x^4+3x^2-2$ 

   Phương pháp giải:

   • Áp dụng qui tắc cộng trừ các đa thức 1 biến

   Lời giải:

   Theo đề bài ta có $M(x)=2x^4-5x^3+7x^2+3x$

   $\begin{array}{l}M(x)+Q(x)=6x^5-x^4+3x^2-2\\ \Rightarrow Q(x)=(6x^5-x^4+3x^2-2)-(2x^4-5x^3+7x^2+3x)\\ \Rightarrow Q(x)=6x^5-x^4+3x^2-2-2x^4+5x^3-7x^2-3x\\ Q(x)=6x^5-3x^4+5x^3-4x^2-3x-2\end{array}$

   Theo đề bài ta có :

   $\begin{array}{l}N(x)-M(x)=-4x^4-2x^3+6x^2+7\\ \Rightarrow N(x)=-4x^4-2x^3+6x^2+7+2x^4-5x^3+7x^2+3x\\ \Rightarrow N(x)=-2x^4-7x^3+13x^2+3x+7\end{array}$

   Bài 9 trang 42 Toán lớp 7: Thực hiện phép nhân.

   a) $(3x-2)(4x+5)$

   b) $(x^2-5x+4)(6x+1)$

   Phương pháp giải:

   • Áp dụng qui tắc nhân 2 đa thức 1 biến

   Lời giải:

   a) $(3x-2)(4x+5)$

   $\begin{array}{l}=3x(4x+5)-2(4x+5)\\ =3x.4x+5.3x-2.4x-2.5\\ =12x^2+7x-10\end{array}$

   b) $(x^2-5x+4)(6x+1)$

   $\begin{array}{l}=x^2(6x+1)-5x(6x+1)+4(6x+1)\\ =x^2.6x+1.x^2-5x.6x-5x.1+4.6x+4.1\end{array}$

   $=6x^3-29x^2+19x+4$

   Bài 10 trang 42 Toán lớp 7: Thực hiện phép chia.

   a) $(45x^5-5x^4+10x^2):5x^2$

   b) $(9t^2-3t^4+27t^5):3t$ 

   Phương pháp giải:

   • Thực hiện phép tính bằng qui tắc chia đa thức
   • Ta có thể chia theo cột nhưng cần sắp xếp các đa thức theo thứ tự lũy thừa giảm dần

   Lời giải:

   a)      $(45x^5-5x^4+10x^2):5x^2$$=9x^3-x^2+2$

    

   b)     $(9t^2-3t^4+27t^5):3t=(27t^5-3t^4+9t^2):3t=(27t^5):(3t)-(3t^4):(3t)+(9t^2):(3t)=9t^4-3t^3+3t$

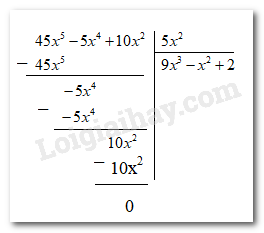
   Bài 11 trang 42 Toán lớp 7: Thực hiện phép chia.

   a) $(2y^4-13y^3+15y^2+11y-3):(y^2-4y-3)$

   b) $(5x^3-3x^2+10):(x^2+1)$

   Phương pháp giải:

   Đặt tính và chia 2 đa thức

   Ta sắp xếp các đa thức theo thứ tự giảm dần của lũy thừa để dễ thực hiện phép tính hơn

   Lời giải:

   

   $a)(2y^4-13y^3+15y^2+11y-3):(y^2-4y-3)=2y^2-5y+1$

   b) $(5x^3-3x^2+10):(x^2+1)=5x-3+\frac{-5x+13}{x^2+1}$

   Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

   Bài 1: Biểu thức số và biểu thức đại số

   Bài 2: Đa thức một biến

   Bài 3: Phép cộng và phép trừ đa thức một biến

   Bài 4: Phép nhân và phép chia đa thức một biến
3. Sách bài tập Toán 7 Bài tập cuối chương 7 (Chân trời sáng tạo)
   Giải SBT Toán lớp 7 Bài tập cuối chương 7

   Giải trang 33 Tập 2

   Bài 1 trang 33 Tập 2:Cho B = xy³ + 4xy – 2x² + 3. Tính giá trị của biểu thức B khi x = –1, y = 2.

   Lời giải:

   Khi x = –1, y = 2 thay vào biểu thức B ta được:

   B = (–1) . 2³ + 4 . (–1) . 2 – 2 . (–1)² + 3

       = –8 – 8 – 2 + 3

       = –15.

   Vậy giá trị của biểu thức B khi x = –1, y = 2 là B = –15.

   Bài 2 trang 33 Tập 2:Trong các biểu thức sau, biểu thức nào là đơn thức một biến?

   a) 2y;           b) 3x + 5;               c) 12;           d) $\frac{1}{3}$ t².

   Lời giải:

   Ta có:

   + Biểu thức a) là đơn thức một biến của biến y;

   + Biểu thức b) là đa thức một biến của biến x;

   + Biểu thức c) là đơn thức một biến.

   + Biểu thức d) là đơn thức một biến của biến t.

   Vậy trong các biểu thức trên, biểu thức a), c), d) là đơn thức một biến.

   Bài 3 trang 33 Tập 2:Trong các biểu thức sau, biểu thức nào là đa thức một biến?

   5 – 2x;         6x² + 8x³ + 3x – 2;            $\frac{2}{x-1}$;          $\frac{1}{4}$ t – 5.

   Lời giải:

   Ta có:

   + Biểu thức 5 – 2x là đa thức một biến của biến x;

   + Biểu thức 6x² + 8x³ + 3x – 2 là đa thức một biến của biến x;

   + Biểu thức $\frac{2}{x-1}$  không phải là đa thức một biến;

   + Biểu thức $\frac{1}{4}$ t – 5 là đa thức một biến của biến t.

   Vậy trong các biểu thức trên, các biểu thức là đa thức một biến là: 5 – 2x; 6x² + 8x³ + 3x – 2; $\frac{1}{4}$ t – 5.

   Bài 4 trang 33 Tập 2:Hãy viết một đa thức một biến bậc bốn có 5 số hạng.

   Lời giải:

   Đa thức một biến bậc bốn có 5 số hạng là:

   A(x) = x⁴ – 2x³ + 3x² – 4x + 5.

   Nhận xét: Bài này có nhiều cách trả lời.

   Bài 5 trang 33 Tập 2:Hãy nêu bậc của các đa thức sau:

   A = 5x² – 2x⁴ + 7;            B = 17;                  C = 3x – 4x³ + 2x² + 1.

   Lời giải:

   • Ta có:

   A = 5x² – 2x⁴ + 7

       = – 2x⁴ + 5x² + 7

   Đa thức A có bậc là 4 (vì số mũ lớn nhất của biến x là 4).

   • Đa thức B = 17 có bậc là 0 (vì đa thức chỉ có số, không có biến x nên số mũ lớn nhất của biến là 0).

   • Ta có:

   C = 3x – 4x³ + 2x² + 1

       = – 4x³ + 2x² + 3x + 1

   Đa thức C có bậc là 3 (vì số mũ lớn nhất của biến x là 3).

   Bài 6 trang 33 Tập 2:Cho đa thức P(x) = x³ + 64. Tìm nghiệm của P(x) trong tập hợp {0; 4; –4}. 

   Lời giải:

   Cách 1: Xét đa thức P(x) = x³ + 64.

   • Với x = 0 thay vào P(x) ta có:

   P(0) = 0³ + 64 = 64.

   Do đó x = 0 không là nghiệm của P(x).

   • Với x = 4 thay vào P(x) ta có:

   P(4) = 4³ + 64 = 64 + 64 = 128.

   Do đó x = 4 không là nghiệm của P(x).

   • Với x = –4 thay vào P(x) ta có:

   P(–4) = (–4)³ + 64 = –64 + 64 = 0.

   Do đó x = –4 là nghiệm của P(x).

   Vậy trong các số thuộc tập hợp {0; 4; –4} thì có –4 là nghiệm của P(x).

   Cách 2: Xét đa thức P(x) = x³ + 64.

   Ta có P(x) = 0

   Hay x³ + 64 = 0

   Suy ra x³ = –64 = (–4)³

   Do đó x = –4.

   Vậy trong các số thuộc tập hợp {0; 4; –4} thì số –4 là nghiệm của P(x).

   Bài 7 trang 33 Tập 2:Tam giác có độ dài hai cạnh là 3y + 2; 6y – 4 và chu vi bằng 23y – 5. Tìm cạnh chưa biết trong tam giác đó.

   Lời giải:

   Gọi A(y) là biểu thức biểu thị độ dài cạnh chưa biết trong tam giác đó.

   Khi đó chu vi của tam giác đó là:

   (3y + 2) + (6y – 4) + A(y)

   = (3y + 6y) + (2 – 4) + A(y)

   = 9y – 2 + A(y).

   Mà theo bài tam giác đó có chu vi bằng 23y – 5 nên ta có:

   9y – 2 + A(y) = 23y – 5

   Suy ra A(y) = 23y – 5 – (9y – 2)

                       = 23y – 5 – 9y + 2

                       = (23y – 9y) + (–5 + 2)

                       = 14y – 3.

   Vậy độ dài cạnh chưa biết trong tam giác đó là A(y) = 14y – 3.

   Giải trang 34 Tập 2

   Bài 8 trang 34 Tập 2:Cho đa thức M(x) = 3x⁵ – 4x³ + 9x + 2. Tìm các đa thức N(x), Q(x) sao cho: N(x) – M(x) = –5x⁴ – 4x³ + 2x² + 8x và Q(x) + M(x) = 3x⁴ – 2x³ + 9x² – 7.

   Lời giải:

   • Ta có: N(x) – M(x) = –5x⁴ – 4x³ + 2x² + 8x

   Suy ra N(x) = –5x⁴ – 4x³ + 2x² + 8x + M(x)

   Do đó N(x) = –5x⁴ – 4x³ + 2x² + 8x + (3x⁵ – 4x³ + 9x + 2)

                       = –5x⁴ – 4x³ + 2x² + 8x + 3x⁵ – 4x³ + 9x + 2

                       = 3x⁵ – 5x⁴ + (–4x³ – 4x³) + 2x² + (8x + 9x) + 2

                       = 3x⁵ – 5x⁴ – 8x³ + 2x² + 17x + 2.

   • Ta có: Q(x) + M(x) = 3x⁴ – 2x³ + 9x² – 7.

   Suy ra Q(x) = 3x⁴ – 2x³ + 9x² – 7 – M(x)

   Do đó Q(x) = 3x⁴ – 2x³ + 9x² – 7 – (3x⁵ – 4x³ + 9x + 2)

                       = 3x⁴ – 2x³ + 9x² – 7 – 3x⁵ + 4x³ – 9x – 2

                       = – 3x⁵ + 3x⁴ + (– 2x³ + 4x³) + 9x² – 9x + (– 7 – 2)

                       = – 3x⁵ + 3x⁴ + 2x³ + 9x² – 9x – 9.

   Vậy N(x) = 3x⁵ – 5x⁴ – 8x³ + 2x² + 17x + 2;

   Q(x) = – 3x⁵ + 3x⁴ + 2x³ + 9x² – 9x – 9.

   Bài 9 trang 34 Tập 2:Thực hiện phép nhân.

   a) (4x – 5)(3x + 4);

   b) (2x² – 3x + 5)(4x + 3).

   Lời giải:

   a) (4x – 5)(3x + 4)

   = 4x(3x + 4) – 5(3x + 4)

   = 12x² + 16x – 15x – 20

   = 12x² + (16x – 15x) – 20

   = 12x² + x – 20.

   Vậy (4x – 5)(3x + 4) = 12x² + x – 20.

   b) (2x² – 3x + 5)(4x + 3)

   = 2x²(4x + 3) – 3x(4x + 3) + 5(4x + 3)

   = 8x³ + 6x² – 12x² – 9x + 20x + 15

   = 8x³ + (6x² – 12x²) + (– 9x + 20x) + 15

   = 8x³ – 6x² + 11x + 15.

   Vậy (2x² – 3x + 5)(4x + 3) = 8x³ – 6x² + 11x + 15.

   Bài 10 trang 34 Tập 2:Thực hiện phép chia.

   a) (64y² – 16y⁴ + 8y⁵) : 4y;

   b) (5t² – 8t + 3) : (t – 1).

   Lời giải:

   a) (64y² – 16y⁴ + 8y⁵) : 4y;

   = (64y² : 4y) + (–16y⁴ : 4y) + (8y⁵ : 4y)

   = 16y – 4y³ + 2y⁴.

   Vậy (64y² – 16y⁴ + 8y⁵) : 4y = 16y – 4y³ + 2y⁴.

   b) (5t² – 8t + 3) : (t – 1)

   Thực hiện đặt tính phép chia đa thức như sau:

   

    

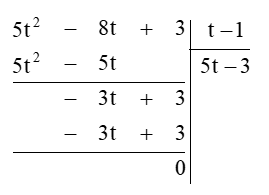
   Vậy (5t² – 8t + 3) : (t – 1) = 5t – 3.

   Bài 11 trang 34 Tập 2:Thực hiện phép chia.

   a) (x⁴ + 6x² + 8) : (x² + 2);

   b) (3x³ – 2x² + 3x – 2) : (x² + 1).

   Lời giải:

   a) (x⁴ + 6x² + 8) : (x² + 2)

   Thực hiện đặt tính phép chia đa thức như sau:

   

    

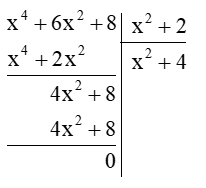
   Vậy (x⁴ + 6x² + 8) : (x² + 2) = x² + 4.

   b) (3x³ – 2x² + 3x – 2) : (x² + 1)

   Thực hiện đặt tính phép chia đa thức như sau:

   

    

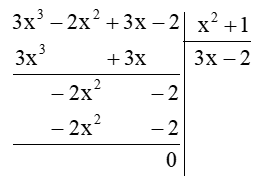
   Vậy (3x³ – 2x² + 3x – 2) : (x² + 1) = 3x – 2.

   Bài 12 trang 34 Tập 2:Thực hiện phép chia.

   a) (2x² – 7x + 4) : (x – 2);

   b) (2x³ + 3x² + 3x + 4) : (x² + 2).

   Lời giải:

   a) (2x² – 7x + 4) : (x – 2)

   Thực hiện đặt tính phép chia đa thức như sau:

   

    

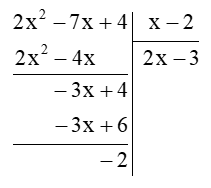
   Vậy $\frac{2x^2-7x+4}{x-2}=2x-3-\frac{2}{x-2}.$

   b) (2x³ + 3x² + 3x + 4) : (x² + 2).

   Thực hiện đặt tính phép chia đa thức như sau:

   

    

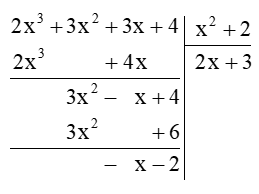
   Vậy  $\frac{2x^3+3x^2+3x+4}{x^2+2}=2x+3-\frac{x+2}{x^2+2}.$

   Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

   Bài 4 : Phép nhân và phép chia đa thức một biến

   Bài tập cuối chương 7

   Bài 1 : Góc và cạnh của một tam giác

   Bài 2 : Tam giác bằng nhau

   Bài 3 : Tam giác cân
4. 30 câu Trắc nghiệm Chương 7: Biểu thức đại số (Chân trời sáng tạo) có đáp án 2023 – Toán lớp 7
   Trắc nghiệm Toán 7 Chương 7: Biểu thức đại số

   Câu 1. Trong các biểu thức sau đây, có bao nhiêu đa thức một biến:

   2 ; $\frac{2}{y}$ ; 3x² − 2 ; $\frac{x-2}{3x^2-1}$ .

   A. 1;

   B. 2;

   C. 3;

   D. 4.

   Hướng dẫn giải

   Đáp án đúng là: B

   Theo định nghĩa, đa thức một biến là tổng của những đơn thức cùng một biến và đơn thức một biến cũng là đa thức một biến.

   Do đó chỉ có 2 và 3x² − 2 là đa thức một biến.

   Vậy trong 4 đa thức trên có 2 đa thức một biến.

   Câu 2. Tìm bậc của đa thức sau: y − 3 +5y² − 6y⁵ + y⁴.

   A. 1;

   B. 2;

   C. 4;

   D. 5.

   Hướng dẫn giải

   Đáp án đúng là: D

   Trong đa thức trên, số mũ cao nhất của y là 5.

   Do đó bậc của đa thức đã cho là 5.

   Câu 3. Tập các nghiệm của đa thức B(x) = 3x² − 12 trong tập hợp {0; 2; −2; 3} là:

   A.{0; 2};

   B. {0; 3};

   C. {2; −2};

   D. {2}.

   Hướng dẫn giải

   Đáp án đúng là: C

   Theo định nghĩa: Nếu đa thức B(x) có giá trị bằng 0 tại x = a thì ta nói a là một nghiệm của đa thức đó.

   Thay từng phần tử trong tập hợp trên vào đa thức B(x) ta được:

   B(0) = 3 . 0² − 12 = −12;

   B(2) = 3 . 2² − 12 = 3 . 4 − 12 = 12 − 12 = 0;

   B(−2) = 3 . (−2)² − 12 = 3 . 4 − 12 = 12 − 12 = 0;

   B(3) = 3 . 3² − 12 = 3 . 9 − 12 = 27 − 12 = 15.

   Vậy {2; −2} là nghiệm của đa thức B(x).

   Câu 4. Cho hai đa thức:M(x) = x³ − 2x + 1 và N(x) = x² + 2x − 5. Tính M(x) + N(x).

   A. x³ − 4x − 4;

   B. x³ + x² − 6;

   C. x³ + x² − 4x − 4;

   D. x³ + x² − 4.

   Hướng dẫn giải

   Đáp án đúng là: D

   M(x) + N(x) = (x³ − 2x + 1) + (x² + 2x − 5)

   = x³ − 2x + 1 + x² + 2x − 5

   = x³ + x² + (−2x + 2x) + (1 − 5)

   = x³ + x² – 4.

   Câu 5. Cho đa thức A(x) = x⁴ + 3x³ + 2x; B(x) = x³ + 2; C(x) = −x⁴ + 2x³ − 9 .

   Tính A(x) − B(x) + C(x).

   A. 4x³ + 2x − 11;

   B. 4x³ − 2x − 11;

   C. 2x⁴ + 4x³ + 2x − 11;

   D. 4x³ + 2x + 11.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: A(x) − B(x) + C(x)

   = (x⁴ + 3x³ + 2x) − (x³ + 2) + (−x⁴ + 2x³ − 9)

   = x⁴ + 3x³ + 2x − x³ − 2 − x⁴ + 2x³ − 9

   = (x⁴ − x⁴) + (3x³ − x³ + 2x³) + 2x + (− 2 − 9)

   = 4x³ + 2x – 11.

   Câu 6. Cho biểu thức: 2x² − x(2x + 3) + 3 . (x + 2). Sau khi rút gọn thì biểu thức trở thành:

   A. 6;

   B. 2x² − 3x;

   C. 0;

   D. 3x.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 2x² − x(2x + 3) + 3 . (x + 2)

   = 2x² − 2x² − 3x + 3x + 6

   = (2x² − 2x²) +(− 3x + 3x) + 6= 6.

   Câu 7. Tính giá trị của biểu thức A = x² (y − 2) + 7xy + 10y² khi x = 2; y = 1

   A. 16;

   B. 18;

   C. 20;

   D. 10.

   Hướng dẫn giải

   Đáp án đúng là: C

   Thay x = 2; y = 3 vào biểu thức A, ta được:

   A = 2² . (1 − 2) + 7 . 2 . 1 + 10 . 1²

   = 4 . (−1) + 14 + 10

   = −4 + 14 + 10 = 20.

   Câu 8. Biểu thức số của diện tích hình tam giác có chiều cao bằng 3 và cạnh đáy bằng 5 là:

   A. 3 . 5;

   B. $\frac{3.5}{2}$ ;

   C. 2 . 2 . 5;

   D. 2 . 5.

   Hướng dẫn giải

   Đáp án đúng là: B

   

   Diện tích hình tam giác bằng tích của chiều cao nhân độ dài đáy chia cho 2nên ta có biểu thức số $\frac{3.5}{2}$ biểu thị diện tích tam giác .

   Câu 9.Trong túi có 3 màu bi gồm: màu xanh, màu đỏ và màu vàng. Số viên bi xanh là 5x² + 3, số viên bi đỏ là 2x² + 3x và số viên bi vàng là 5. Biểu thức đại số biểu thị tổng số viên bi trong túi là biểu thức nào trong các biểu thức sau đây?

   A. 5x² + 3x + 8;

   B. 7x² + 3x + 3;

   C. 7x² + 3x + 8;

   D. 7x² + 8x + 5.

   Hướng dẫn giải

   Đáp án đúng là: C

   Tổng số viên bi trong túi là:

   (5x² + 3) + (2x² + 3x) + 5

   = 5x² + 3 + 2x² + 3x + 5

   = (5x² + 2x²) + 3x + (5 + 3)

   = 7x² + 3x + 8.

   Biểu thức đại số biểu thị tổng số viên bi trong túi là: 7x² + 3x + 8.

   Câu 10. Trong các biểu thức sau đây, biểu thức nào là đơn thức một biến?

   A. x² + 2x + 1;

   B. 4y + 12;

   C.9x;

   D. y³ + 13y − 5.

   Hướng dẫn giải

   Đáp án đúng là: C

   Đơn thức một biến là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và biến đó .

   Do đó 9x là đơn thức một biến.

   Câu 11. Trong kì thi học sinh giỏi, học sinh tại các trường thuộc Thành phố Hồ Chí Minh được các huy chương sau: vàng, bạc, đồng. Trong đó số huy chương vàng bằng 2x⁴ − x² + 3, số huy chương bạc bằng x³ − 1. Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh, biết tổng tất cả các huy chương bằng 3x⁴ + x³ − 5.

   A. x⁴ + x² − 7;

   B. x⁴ + x² + 7;

   C. x⁴ + 2x² − 7;

   D.x⁴ + x³ − x² − 7.

   Hướng dẫn giải

   Đáp án đúng là: A

   Biểu thức biểu thị tổng số huy chương vàng và bạccủa các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:

   (2x⁴ − x² + 3) + (x³ − 1)

   = 2x⁴ − x² + 3 + x³ − 1

   = 2x⁴ + x³ − x² + (3 − 1)

   = 2x⁴ + x³ − x² + 2.

   Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:

   3x⁴ + x³ − 5 − (2x⁴ + x³ − x² + 2)

   = 3x⁴ + x³ − 5 − 2x⁴ − x³ + x² − 2

   = (3x⁴ − 2x⁴) + (x³ − x³) + x² + (−5 − 2)

   = x⁴ + x² – 7.

   Vậy biểu thức biểu thị số huy chương đồng của học sinh tại các trường thuộc Thành phố Hồ Chí Minh là x⁴ + x² – 7.

   Câu 12. Cho biểu thức sau: (5 − x) + [(−14 − 5x²) + (9 + x)]. Rút gọn biểu thức đã cho ta được biểu thức nào trong các biểu thức sau đây?

   A. 5x²;

   B. −5x²;

   C. x² − 5;

   D. x².

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: (5 − x) + [(−14 − 5x²) + (9 + x)]

   = 5 − x − 14 − 5x² + 9 + x

   = − 5x² + (x – x) + (5 − 14 + 9)

   = −5x².

   Câu 13. Tích của hai đa thức −3x + 2 và 7x − 5 là:

   A. 21x² + 29x − 10;

   B. −21x² + 29x − 10;

   C. 21x² + 29x + 10;

   D. −21x² + 19x − 10.

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: (−3x + 2)(7x − 5)

   = (−3x) . (7x − 5) + 2 . (7x − 5)

   = −21x² + 15x + 14x − 10

   = −21x² + (15x + 14x) − 10

   = −21x² + 29x – 10.

   Câu 14. Tìm a để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x – 3.

   A. 3;

   B. 6;

   C. 4;

   D. −3.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thực hiện phép tính, ta được:

   

   Vậy để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x − 3 thì a + 3 = 0.

   Do đó a = −3 để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x – 3.

   Câu 15. Kết quả của phép tính: 36 . (−x³ + 4x² − 5x) . $\frac{1}{12}$ tại x = 2 là:

   A. −6;

   B. 0;

   C. 6;

   D. 5.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có : 36 . (−x³ + 4x² − 5x) . $\frac{1}{12}$

   = 36 . [(-x³ + 4x² – 5x).$\frac{1}{12}$]

   = 36 . [$\frac{1}{12}$.(-x³ + 4x² – 5x)]

   = (36.$\frac{1}{12}$). (−x³ + 4x² − 5x)

   = 3 . (−x³ + 4x² − 5x)

   = −3x³ + 12x² − 15x (1)

   Thay x = 2 vào (1) ta được:

   (−3) . 2³ + 12 . 2² − 15 . 2

   = (−3) . 8 + 12 . 4 − 15 . 2

   = (−24) + 48 − 30 = −6.

   Vậy kết quả của phép tính: 36 . (−x³ + 4x² − 5x) . tại x = 2 bằng −6.

   Câu 16. Biểu thức số biểu thị chu vi hình vuông có cạnh bằng 5 cm là:

   A. 2 . 5;

   B. 4 . 5;

   C. 3 . 5;

   D. 5 . 5.

   Hướng dẫn giải

   Đáp án đúng là: B

   

   Hình vuông có cạnh bằng 5 cm nên biểu thức số của chu vi của hình vuông bằng 4 . 5.

   Câu 17. Rút gọn biểu thức: 5(x² − x) + 2x² + 7x, ta được biểu thức nào trong các biểu thức sau đây?

   A. 7x² + 2x;

   B. 5x²− 5x + 2x² + 7x;

   C. 5x²− 5x;

   D. 2x² − 7x.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 5(x² − x) + 2x² + 7x

   = 5x² − 5x + 2x² + 7x

   = (5 + 2).x² + ( −5 + 7).x

   = 7x² + 2x.

   Câu 18. Giá trị của biểu thức (a − b)² − 2c khi a = 9, b = 4, c = 5 bằng bao nhiêu?

   A. 5;

   B. 10;

   C. 25;

   D. 15.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thay a = 9, b = 4, c = 5 vào biểu thức trên, ta được:

   (9 − 4)² − 2.5 = 5² − 10

   = 25 − 10 = 15.

   Câu 19. Rút gọn biểu thức: 2x(x − y) + 3y(y − x) − 2y² − 2x² ta được biểu thức nào trong các biểu thức sau?

   A. y² − 5xy;

   B. x − 2xy + y²;

   C. −5xy;

   D.2x² + 3y².

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 2x(x − y) + 3y(y − x) − 2y² − 2x²

   = 2x² − 2xy + 3y² − 3xy − 2y² − 2x²

   = (2 − 2).x² + (3 − 2).y² + (−2 − 3).xy

   = y² − 5xy.

   Câu 20. Cho biết giá bán của một chiếc lò vi sóng tại một cửa hàng là T− aT (triệu đồng), với T là giá gốc và a là mã giảm giá áp dụng cho khách hàng thân thiết. Tính giá bán của chiếc lò vi sóng khi được giảm giá với T= 3 (triệu đồng) và a= 10%.

   A. 2 triệu đồng;

   B. 2,7 triệu đồng;

   C. 1 triệuđồng;

   D. 1,5 triệu đồng.

   Hướng dẫn giải

   Đáp án đúng là: B

   Thay T = 3 và a = 10% vào biểu thứcT – aT, ta được:

   T – aT = 3 − 10%. 3 = 3 − 0,3 = 2,7 (triệu đồng)

   Vậy giá bán của chiếc lò vi sóng khi được giảm giá là 2,7 triệu đồng.

   Câu 21. Một thửa ruộng hình chữ nhật (như hình vẽ) có chiều dài bằng 3a, chiều rộng bằng 5b. Người ta xây thêm phần đê xung quanh mảnh ruộng rộng 2 m. Tính diện tích phần đê xung quanh mảnh ruộng, biết a = 5 m, b = 2 m.

   

   A. 150 m²;

   B. 66m²;

   C. 40 m²;

   D. 84 m².

   Hướng dẫn giải

   Đáp án đúng là: D

   Diện tích thửa ruộng ban đầu là:

   3a . 2b = 3 . 5 . 5 . 2 = 150 (m²)

   Diện tích còn lại của mảnh ruộng là:

   (3a − 2 − 2) . (5b − 2 − 2)

   = (3 . 5 − 2 − 2) . (5 . 2 − 2 − 2)

   = 11 . 6 = 66 (m²)

   Diện tích phần đê xung quanh là:

   150 − 66 = 84 (m²).

   Vậy diện tích phần đê xung quanh mảnh ruộng bằng 84 m².

   Câu 22. Cho hai đa thức A(x) = − 2x + 1 và B(x) = 5x² + 2x + 9. Tính C(x) tại x = 2 biết C(x) = A(x) + B(x).

   A. 30;

   B. 40;

   C. 23;

   D. 10.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: C(x) = A(x) + B(x)

   = − 2x + 1 + (5x² + 2x + 9)

   = − 2x + 1 + 5x² + 2x + 9

   = 5x² + 10.

   Ta có: C(2) = 5 . 2² +10 = 5.4 + 10

   = 20 + 10 = 30.

   Câu 23.Cho đa thức: P(y) = y² − 10 + 3y² − 9y + 4 − 7y.

   Rút gọn biểu thức sau và sắp xếp theo lũy thừa tăng của biến y, ta được đa thức nào trong các đa thức sau đây?

   A. y² − 10 − 9y;

   B. 6 − 2y + 4y²;

   C. − 6 − 16y + 4y²;

   D. − 6 + 16y + 4y².

   Hướng dẫn giải

   Đáp án đúng là: C

   Ta có: P(y) = y² − 10 + 3y² − 9y + 4 − 7y

   = −10 + 4 − 9y − 7y + y² + 3y²

   = (−10 + 4) + (−9 − 7)y + (1 + 3)y²

   = −6 − 16y + 4y².

   Vậy rút gọn và sắp xếp theo lũy thừa giảm của biến y thì biểu thức: P(y) = −6 − 16y + 4y².

   Câu 24. Diện tích một hình vuông được tính bởi biểu thức S(x) = x². Tính giá trị của S biết x là nghiệm của đa thức P(x) = 2x – 8.

   A. 16;

   B. 25;

   C. 36;

   D. 9.

   Hướng dẫn giải

   Đáp án đúng là: A

   Theo đề bài, x là nghiệm của đa thức P(x) = 2x – 8 nên ta có:

   P(x) = 2x − 8 = 0

   Suy ra x = 4

   Ta có: S(4) = 4² = 16.

   Vậy diện tích hình vuông bằng 16.

   Câu 25. Cho đa thức U(x) = 7x² + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x³ + x² –5.

   A. V(x) = x³ − 6x² − 4x − 2;

   B. V(x) = 6x² − 4x − 2;

   C. V(x) = x³ − 8x² + 5x +13;

   D. V(x) = x³ − 6x² − 2.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: U(x) = 7x² + 4x − 3

   Vì U(x) + V(x) = x³ + x² −5 nên

   V(x) = x³ + x² − 5 − U(x)

   = x³ + x² − 5 − (7x² + 4x − 3)

   = x³ + x² − 5 − 7x² − 4x + 3

   = x³ + (x² − 7x²) − 4x + (−5 + 3)

   = x³ − 6x² − 4x – 2.

   Vậy V(x) = x³ − 6x² − 4x – 2.

   Câu 26. Cho ba đa thức A(x) = x² − 3x +10; B(x) = 3x³ +16; C(x) = 2x⁴ − 4x² − 8x.

   Tính A(x) − B(x) − C(x).

   A. −2x⁴ − 3x³ + 5x² + 5x − 6;

   B. 2x⁴ + 3x³ − 3x² − 11x +26;

   C. −2x⁴ − 3x³ − 3x² + 5x − 6;

   D. −2x⁴ − 3x³ + 5x² − 11x − 6.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: A(x) − B(x) = (x² − 3x +10) − (3x³ +16)

   = x² − 3x + 10 − 3x³ − 16

   = − 3x³ + x² − 3x + (10 − 16)

   = − 3x³ + x² − 3x – 6.

   Khi đó: A(x) − B(x) − C(x)

   = (−3x³ + x² − 3x − 6) − (2x⁴ − 4x² − 8x)

   = −3x³ + x² − 3x − 6 − 2x⁴ + 4x² + 8x

   = −2x⁴ − 3x³ + (x² + 4x²) + (−3x + 8x) − 6

   = −2x⁴ − 3x³ + 5x² + 5x – 6.

   Vậy A(x) − B(x) − C(x) = −2x⁴ − 3x³ + 5x² + 5x – 6.

   Câu 27. Biểu thức biểu thị chu vi của hình thang vuông như hình bên dưới là:

   

   A. x² + 6x + 4;

   B. 2x² − 6x + 8;

   C. 2x² + 2x + 8;

   D. 2x² + 6x + 8.

   Hướng dẫn giải

   Đáp án đúng là: D

   Chu vi của hình thang bằng tổng độ dài hai cạnh đáy và hai cạnh bên. Khi đó:

   P = (4x −2 + x² + 6) + (2x + 3 + x² + 1) (với P là chu vi của hình thang)

   = 4x − 2 + x² + 6 + 2x + 3 + x² + 1

   = (x² + x²) + (4x + 2x)+ (−2 + 6 + 3 + 1)

   = 2x² + 6x +8.

   Vậy chu vi của hình thang vuông trên được biểu thị bằng biểu thức 2x² + 6x +8.

   Câu 28.Cho tam giác vuông (như hình bên dưới) có chu vi bằng 14x – 4. Tính cạnh BC của tam giác ABC.

   

   A. 9x − 8;

   B. 9x + 8;

   C. 7x − 8;

   D. 9x + 4.

   Hướng dẫn giải

   Đáp án đúng là: A

   Chu vi tam giác trên bằng tổng độ dài ba cạnh nên ta có:

   P = AB + AC + BC (với P là chu vi của hình tam giác)

   Suy ra BC = P − AB − AC

   = 14x − 4 − (2x +3) − (3x+1)

   = 14x − 4 − 2x − 3 − 3x − 1

   = (14x − 2x − 3x) + (−4 − 3 − 1)

   = 9x – 8.

   Vậy BC = 9x – 8.

   Câu 29. Phép chia đa thức (12x³ + 12x² − 15x − 9) cho đa thức (2x + 1) được đa thức thương là:

   A. 6x² + 3x − 9;

   B. 6x² + 6x − 9;

   C. 6x² + 3x + 9;

   D. 6x² + 5x − 9.

   Hướng dẫn giải

   Đáp án đúng là: A

   Thực hiện phép tính chia, ta được:

   

   Vậy đa thức thương của phép chia đa thức trên bằng 6x² + 3x – 9.

   Câu 30. Thương và phần dư của phép chia đa thức (4x³ − 3x² + 2x + 1) cho đa thức (x² − 1)lần lượt là:

   A. 4x + 3; 6x − 2;

   B. 2x + 3; 3x − 1;

   C.4x − 3; 0;

   D. 4x − 3; 6x − 2.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thực hiện phép tính, ta được:

   

   Vậy phép chia đa thức trên có thương bằng 4x − 3 và phần dư bằng 6x – 2.

   Câu 1. Cho biểu thức: 2x² − x(2x + 3) + 3 . (x + 2). Sau khi rút gọn thì biểu thức trở thành:

    

   A. 6;

   B. 2x² − 3x;

   C. 0;

   D. 3x.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 2x² − x(2x + 3) + 3 . (x + 2)

   = 2x² − 2x² − 3x + 3x + 6

   = (2x² − 2x²) +(− 3x + 3x) + 6= 6.

   Câu 2. Tính giá trị của biểu thức A = x² (y − 2) + 7xy + 10y² khi x = 2; y = 1

   A. 16;

   B. 18;

   C. 20;

   D. 10.

   Hướng dẫn giải

   Đáp án đúng là: C

   Thay x = 2; y = 3 vào biểu thức A, ta được:

   A = 2² . (1 − 2) + 7 . 2 . 1 + 10 . 1²

   = 4 . (−1) + 14 + 10

   = −4 + 14 + 10 = 20.

   Câu 3. Biểu thức số của diện tích hình tam giác có chiều cao bằng 3 và cạnh đáy bằng 5 là:

   A. 3 . 5;

   B. $\frac{3.5}{2}$ ;

   C. 2 . 2 . 5;

   D. 2 . 5.

   Hướng dẫn giải

   Đáp án đúng là: B

   

   Diện tích hình tam giác bằng tích của chiều cao nhân độ dài đáy chia cho 2nên ta có biểu thức số $\frac{3.5}{2}$ biểu thị diện tích tam giác .

   Câu 4.Trong túi có 3 màu bi gồm: màu xanh, màu đỏ và màu vàng. Số viên bi xanh là 5x² + 3, số viên bi đỏ là 2x² + 3x và số viên bi vàng là 5. Biểu thức đại số biểu thị tổng số viên bi trong túi là biểu thức nào trong các biểu thức sau đây?

   A. 5x² + 3x + 8;

   B. 7x² + 3x + 3;

   C. 7x² + 3x + 8;

   D. 7x² + 8x + 5.

   Hướng dẫn giải

   Đáp án đúng là: C

   Tổng số viên bi trong túi là:

   (5x² + 3) + (2x² + 3x) + 5

   = 5x² + 3 + 2x² + 3x + 5

   = (5x² + 2x²) + 3x + (5 + 3)

   = 7x² + 3x + 8.

   Biểu thức đại số biểu thị tổng số viên bi trong túi là: 7x² + 3x + 8.

   Câu 5. Trong các biểu thức sau đây, biểu thức nào là đơn thức một biến?

   A. x² + 2x + 1;

   B. 4y + 12;

   C.9x;

   D. y³ + 13y − 5.

   Hướng dẫn giải

   Đáp án đúng là: C

   Đơn thức một biến là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và biến đó .

   Do đó 9x là đơn thức một biến.

   Câu 6. Trong các biểu thức sau đây, có bao nhiêu đa thức một biến:

   2 ; $\frac{2}{y}$ ; 3x² − 2 ; $\frac{x-2}{3x^2-1}$ .

   A. 1;

   B. 2;

   C. 3;

   D. 4.

   Hướng dẫn giải

   Đáp án đúng là: B

   Theo định nghĩa, đa thức một biến là tổng của những đơn thức cùng một biến và đơn thức một biến cũng là đa thức một biến.

   Do đó chỉ có 2 và 3x² − 2 là đa thức một biến.

   Vậy trong 4 đa thức trên có 2 đa thức một biến.

   Câu 7. Tìm bậc của đa thức sau: y − 3 +5y² − 6y⁵ + y⁴.

   A. 1;

   B. 2;

   C. 4;

   D. 5.

   Hướng dẫn giải

   Đáp án đúng là: D

   Trong đa thức trên, số mũ cao nhất của y là 5.

   Do đó bậc của đa thức đã cho là 5.

   Câu 8. Tập các nghiệm của đa thức B(x) = 3x² − 12 trong tập hợp {0; 2; −2; 3} là:

   A.{0; 2};

   B. {0; 3};

   C. {2; −2};

   D. {2}.

   Hướng dẫn giải

   Đáp án đúng là: C

   Theo định nghĩa: Nếu đa thức B(x) có giá trị bằng 0 tại x = a thì ta nói a là một nghiệm của đa thức đó.

   Thay từng phần tử trong tập hợp trên vào đa thức B(x) ta được:

   B(0) = 3 . 0² − 12 = −12;

   B(2) = 3 . 2² − 12 = 3 . 4 − 12 = 12 − 12 = 0;

   B(−2) = 3 . (−2)² − 12 = 3 . 4 − 12 = 12 − 12 = 0;

   B(3) = 3 . 3² − 12 = 3 . 9 − 12 = 27 − 12 = 15.

   Vậy {2; −2} là nghiệm của đa thức B(x).

   Câu 9. Cho hai đa thức:M(x) = x³ − 2x + 1 và N(x) = x² + 2x − 5. Tính M(x) + N(x).

   A. x³ − 4x − 4;

   B. x³ + x² − 6;

   C. x³ + x² − 4x − 4;

   D. x³ + x² − 4.

   Hướng dẫn giải

   Đáp án đúng là: D

   M(x) + N(x) = (x³ − 2x + 1) + (x² + 2x − 5)

   = x³ − 2x + 1 + x² + 2x − 5

   = x³ + x² + (−2x + 2x) + (1 − 5)

   = x³ + x² – 4.

   Câu 10. Cho đa thức A(x) = x⁴ + 3x³ + 2x; B(x) = x³ + 2; C(x) = −x⁴ + 2x³ − 9 .

   Tính A(x) − B(x) + C(x).

   A. 4x³ + 2x − 11;

   B. 4x³ − 2x − 11;

   C. 2x⁴ + 4x³ + 2x − 11;

   D. 4x³ + 2x + 11.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: A(x) − B(x) + C(x)

   = (x⁴ + 3x³ + 2x) − (x³ + 2) + (−x⁴ + 2x³ − 9)

   = x⁴ + 3x³ + 2x − x³ − 2 − x⁴ + 2x³ − 9

   = (x⁴ − x⁴) + (3x³ − x³ + 2x³) + 2x + (− 2 − 9)

   = 4x³ + 2x – 11.

   Câu 11. Trong kì thi học sinh giỏi, học sinh tại các trường thuộc Thành phố Hồ Chí Minh được các huy chương sau: vàng, bạc, đồng. Trong đó số huy chương vàng bằng 2x⁴ − x² + 3, số huy chương bạc bằng x³ − 1. Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh, biết tổng tất cả các huy chương bằng 3x⁴ + x³ − 5.

   A. x⁴ + x² − 7;

   B. x⁴ + x² + 7;

   C. x⁴ + 2x² − 7;

   D.x⁴ + x³ − x² − 7.

   Hướng dẫn giải

   Đáp án đúng là: A

   Biểu thức biểu thị tổng số huy chương vàng và bạccủa các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:

   (2x⁴ − x² + 3) + (x³ − 1)

   = 2x⁴ − x² + 3 + x³ − 1

   = 2x⁴ + x³ − x² + (3 − 1)

   = 2x⁴ + x³ − x² + 2.

   Biểu thức biểu thị số huy chương đồng của các học sinh tại các trường thuộc Thành phố Hồ Chí Minh là:

   3x⁴ + x³ − 5 − (2x⁴ + x³ − x² + 2)

   = 3x⁴ + x³ − 5 − 2x⁴ − x³ + x² − 2

   = (3x⁴ − 2x⁴) + (x³ − x³) + x² + (−5 − 2)

   = x⁴ + x² – 7.

   Vậy biểu thức biểu thị số huy chương đồng của học sinh tại các trường thuộc Thành phố Hồ Chí Minh là x⁴ + x² – 7.

   Câu 12. Cho biểu thức sau: (5 − x) + [(−14 − 5x²) + (9 + x)]. Rút gọn biểu thức đã cho ta được biểu thức nào trong các biểu thức sau đây?

   A. 5x²;

   B. −5x²;

   C. x² − 5;

   D. x².

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: (5 − x) + [(−14 − 5x²) + (9 + x)]

   = 5 − x − 14 − 5x² + 9 + x

   = − 5x² + (x – x) + (5 − 14 + 9)

   = −5x².

   Câu 13. Tích của hai đa thức −3x + 2 và 7x − 5 là:

   A. 21x² + 29x − 10;

   B. −21x² + 29x − 10;

   C. 21x² + 29x + 10;

   D. −21x² + 19x − 10.

   Hướng dẫn giải

   Đáp án đúng là: B

   Ta có: (−3x + 2)(7x − 5)

   = (−3x) . (7x − 5) + 2 . (7x − 5)

   = −21x² + 15x + 14x − 10

   = −21x² + (15x + 14x) − 10

   = −21x² + 29x – 10.

   Câu 14. Tìm a để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x – 3.

   A. 3;

   B. 6;

   C. 4;

   D. −3.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thực hiện phép tính, ta được:

   

   Vậy để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x − 3 thì a + 3 = 0.

   Do đó a = −3 để đa thức 6x³ + 3x² − 6x + a chia hết cho 3x – 3.

   Câu 15. Kết quả của phép tính: 36 . (−x³ + 4x² − 5x) . $\frac{1}{12}$ tại x = 2 là:

   A. −6;

   B. 0;

   C. 6;

   D. 5.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có : 36 . (−x³ + 4x² − 5x) . $\frac{1}{12}$

   = 36 . [(-x³ + 4x² – 5x).$\frac{1}{12}$]

   = 36 . [$\frac{1}{12}$.(-x³ + 4x² – 5x)]

   = (36.$\frac{1}{12}$). (−x³ + 4x² − 5x)

   = 3 . (−x³ + 4x² − 5x)

   = −3x³ + 12x² − 15x (1)

   Thay x = 2 vào (1) ta được:

   (−3) . 2³ + 12 . 2² − 15 . 2

   = (−3) . 8 + 12 . 4 − 15 . 2

   = (−24) + 48 − 30 = −6.

   Vậy kết quả của phép tính: 36 . (−x³ + 4x² − 5x) . tại x = 2 bằng −6.

   Câu 16. Biểu thức số biểu thị chu vi hình vuông có cạnh bằng 5 cm là:

   A. 2 . 5;

   B. 4 . 5;

   C. 3 . 5;

   D. 5 . 5.

   Hướng dẫn giải

   Đáp án đúng là: B

   

   Hình vuông có cạnh bằng 5 cm nên biểu thức số của chu vi của hình vuông bằng 4 . 5.

   Câu 17. Rút gọn biểu thức: 5(x² − x) + 2x² + 7x, ta được biểu thức nào trong các biểu thức sau đây?

   A. 7x² + 2x;

   B. 5x²− 5x + 2x² + 7x;

   C. 5x²− 5x;

   D. 2x² − 7x.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 5(x² − x) + 2x² + 7x

   = 5x² − 5x + 2x² + 7x

   = (5 + 2).x² + ( −5 + 7).x

   = 7x² + 2x.

   Câu 18. Giá trị của biểu thức (a − b)² − 2c khi a = 9, b = 4, c = 5 bằng bao nhiêu?

   A. 5;

   B. 10;

   C. 25;

   D. 15.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thay a = 9, b = 4, c = 5 vào biểu thức trên, ta được:

   (9 − 4)² − 2.5 = 5² − 10

   = 25 − 10 = 15.

   Câu 19. Rút gọn biểu thức: 2x(x − y) + 3y(y − x) − 2y² − 2x² ta được biểu thức nào trong các biểu thức sau?

   A. y² − 5xy;

   B. x − 2xy + y²;

   C. −5xy;

   D.2x² + 3y².

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: 2x(x − y) + 3y(y − x) − 2y² − 2x²

   = 2x² − 2xy + 3y² − 3xy − 2y² − 2x²

   = (2 − 2).x² + (3 − 2).y² + (−2 − 3).xy

   = y² − 5xy.

   Câu 20. Cho biết giá bán của một chiếc lò vi sóng tại một cửa hàng là T− aT (triệu đồng), với T là giá gốc và a là mã giảm giá áp dụng cho khách hàng thân thiết. Tính giá bán của chiếc lò vi sóng khi được giảm giá với T= 3 (triệu đồng) và a= 10%.

   A. 2 triệu đồng;

   B. 2,7 triệu đồng;

   C. 1 triệuđồng;

   D. 1,5 triệu đồng.

   Hướng dẫn giải

   Đáp án đúng là: B

   Thay T = 3 và a = 10% vào biểu thứcT – aT, ta được:

   T – aT = 3 − 10%. 3 = 3 − 0,3 = 2,7 (triệu đồng)

   Vậy giá bán của chiếc lò vi sóng khi được giảm giá là 2,7 triệu đồng.

   Câu 21. Một thửa ruộng hình chữ nhật (như hình vẽ) có chiều dài bằng 3a, chiều rộng bằng 5b. Người ta xây thêm phần đê xung quanh mảnh ruộng rộng 2 m. Tính diện tích phần đê xung quanh mảnh ruộng, biết a = 5 m, b = 2 m.

   

   A. 150 m²;

   B. 66m²;

   C. 40 m²;

   D. 84 m².

   Hướng dẫn giải

   Đáp án đúng là: D

   Diện tích thửa ruộng ban đầu là:

   3a . 2b = 3 . 5 . 5 . 2 = 150 (m²)

   Diện tích còn lại của mảnh ruộng là:

   (3a − 2 − 2) . (5b − 2 − 2)

   = (3 . 5 − 2 − 2) . (5 . 2 − 2 − 2)

   = 11 . 6 = 66 (m²)

   Diện tích phần đê xung quanh là:

   150 − 66 = 84 (m²).

   Vậy diện tích phần đê xung quanh mảnh ruộng bằng 84 m².

   Câu 22. Cho hai đa thức A(x) = − 2x + 1 và B(x) = 5x² + 2x + 9. Tính C(x) tại x = 2 biết C(x) = A(x) + B(x).

   A. 30;

   B. 40;

   C. 23;

   D. 10.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: C(x) = A(x) + B(x)

   = − 2x + 1 + (5x² + 2x + 9)

   = − 2x + 1 + 5x² + 2x + 9

   = 5x² + 10.

   Ta có: C(2) = 5 . 2² +10 = 5.4 + 10

   = 20 + 10 = 30.

   Câu 23.Cho đa thức: P(y) = y² − 10 + 3y² − 9y + 4 − 7y.

   Rút gọn biểu thức sau và sắp xếp theo lũy thừa tăng của biến y, ta được đa thức nào trong các đa thức sau đây?

   A. y² − 10 − 9y;

   B. 6 − 2y + 4y²;

   C. − 6 − 16y + 4y²;

   D. − 6 + 16y + 4y².

   Hướng dẫn giải

   Đáp án đúng là: C

   Ta có: P(y) = y² − 10 + 3y² − 9y + 4 − 7y

   = −10 + 4 − 9y − 7y + y² + 3y²

   = (−10 + 4) + (−9 − 7)y + (1 + 3)y²

   = −6 − 16y + 4y².

   Vậy rút gọn và sắp xếp theo lũy thừa giảm của biến y thì biểu thức: P(y) = −6 − 16y + 4y².

   Câu 24. Diện tích một hình vuông được tính bởi biểu thức S(x) = x². Tính giá trị của S biết x là nghiệm của đa thức P(x) = 2x – 8.

   A. 16;

   B. 25;

   C. 36;

   D. 9.

   Hướng dẫn giải

   Đáp án đúng là: A

   Theo đề bài, x là nghiệm của đa thức P(x) = 2x – 8 nên ta có:

   P(x) = 2x − 8 = 0

   Suy ra x = 4

   Ta có: S(4) = 4² = 16.

   Vậy diện tích hình vuông bằng 16.

   Câu 25. Cho đa thức U(x) = 7x² + 4x − 3. Tìm đa thức V(x) sao cho U(x) + V(x) = x³ + x² –5.

   A. V(x) = x³ − 6x² − 4x − 2;

   B. V(x) = 6x² − 4x − 2;

   C. V(x) = x³ − 8x² + 5x +13;

   D. V(x) = x³ − 6x² − 2.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: U(x) = 7x² + 4x − 3

   Vì U(x) + V(x) = x³ + x² −5 nên

   V(x) = x³ + x² − 5 − U(x)

   = x³ + x² − 5 − (7x² + 4x − 3)

   = x³ + x² − 5 − 7x² − 4x + 3

   = x³ + (x² − 7x²) − 4x + (−5 + 3)

   = x³ − 6x² − 4x – 2.

   Vậy V(x) = x³ − 6x² − 4x – 2.

   Câu 26. Cho ba đa thức A(x) = x² − 3x +10; B(x) = 3x³ +16; C(x) = 2x⁴ − 4x² − 8x.

   Tính A(x) − B(x) − C(x).

   A. −2x⁴ − 3x³ + 5x² + 5x − 6;

   B. 2x⁴ + 3x³ − 3x² − 11x +26;

   C. −2x⁴ − 3x³ − 3x² + 5x − 6;

   D. −2x⁴ − 3x³ + 5x² − 11x − 6.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có: A(x) − B(x) = (x² − 3x +10) − (3x³ +16)

   = x² − 3x + 10 − 3x³ − 16

   = − 3x³ + x² − 3x + (10 − 16)

   = − 3x³ + x² − 3x – 6.

   Khi đó: A(x) − B(x) − C(x)

   = (−3x³ + x² − 3x − 6) − (2x⁴ − 4x² − 8x)

   = −3x³ + x² − 3x − 6 − 2x⁴ + 4x² + 8x

   = −2x⁴ − 3x³ + (x² + 4x²) + (−3x + 8x) − 6

   = −2x⁴ − 3x³ + 5x² + 5x – 6.

   Vậy A(x) − B(x) − C(x) = −2x⁴ − 3x³ + 5x² + 5x – 6.

   Câu 27. Biểu thức biểu thị chu vi của hình thang vuông như hình bên dưới là:

   

   A. x² + 6x + 4;

   B. 2x² − 6x + 8;

   C. 2x² + 2x + 8;

   D. 2x² + 6x + 8.

   Hướng dẫn giải

   Đáp án đúng là: D

   Chu vi của hình thang bằng tổng độ dài hai cạnh đáy và hai cạnh bên. Khi đó:

   P = (4x −2 + x² + 6) + (2x + 3 + x² + 1) (với P là chu vi của hình thang)

   = 4x − 2 + x² + 6 + 2x + 3 + x² + 1

   = (x² + x²) + (4x + 2x)+ (−2 + 6 + 3 + 1)

   = 2x² + 6x +8.

   Vậy chu vi của hình thang vuông trên được biểu thị bằng biểu thức 2x² + 6x +8.

   Câu 28.Cho tam giác vuông (như hình bên dưới) có chu vi bằng 14x – 4. Tính cạnh BC của tam giác ABC.

   

   A. 9x − 8;

   B. 9x + 8;

   C. 7x − 8;

   D. 9x + 4.

   Hướng dẫn giải

   Đáp án đúng là: A

   Chu vi tam giác trên bằng tổng độ dài ba cạnh nên ta có:

   P = AB + AC + BC (với P là chu vi của hình tam giác)

   Suy ra BC = P − AB − AC

   = 14x − 4 − (2x +3) − (3x+1)

   = 14x − 4 − 2x − 3 − 3x − 1

   = (14x − 2x − 3x) + (−4 − 3 − 1)

   = 9x – 8.

   Vậy BC = 9x – 8.

   Câu 29. Phép chia đa thức (12x³ + 12x² − 15x − 9) cho đa thức (2x + 1) được đa thức thương là:

   A. 6x² + 3x − 9;

   B. 6x² + 6x − 9;

   C. 6x² + 3x + 9;

   D. 6x² + 5x − 9.

   Hướng dẫn giải

   Đáp án đúng là: A

   Thực hiện phép tính chia, ta được:

   

   Vậy đa thức thương của phép chia đa thức trên bằng 6x² + 3x – 9.

   Câu 30. Thương và phần dư của phép chia đa thức (4x³ − 3x² + 2x + 1) cho đa thức (x² − 1)lần lượt là:

   A. 4x + 3; 6x − 2;

   B. 2x + 3; 3x − 1;

   C.4x − 3; 0;

   D. 4x − 3; 6x − 2.

   Hướng dẫn giải

   Đáp án đúng là: D

   Thực hiện phép tính, ta được:

   

   Vậy phép chia đa thức trên có thương bằng 4x − 3 và phần dư bằng 6x – 2.

   Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:

   Trắc nghiệm Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến

   Trắc nghiệm Ôn tập chương 7

   Trắc nghiệm Toán 7 Bài 1: Góc và cạnh của một tam giác

   Trắc nghiệm Toán 7 Bài 2: Tam giác bằng nhau

   Trắc nghiệm Toán 7 Bài 3: Tam giác cân
5. Giải SGK Toán 7 (Kết nối tri thức) Bài tập cuối chương 7
   Giải bài tập Toán lớp 7 Bài tập cuối chương 7

   Giải Toán 7 trang 46 Tập 2

   Bài 7.42 trang 46 Toán lớp 7: Một hãng taxi quy định giá cước như sau: 0,5 km đầu tiên giá 8 000 đồng; tiếp theo cứ mỗi kilomet giá 11 000 đồng. Giả sử một người thuê xe đi x (km)

   a) Chứng tỏ rằng biểu thức biểu thị số tiền mà người đó phải trả là một đa thức. Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức đó.

   b) Giá trị của đa thức tại x = 9 nói lên điều gì?

   Phương pháp giải:

   a) Tìm đa thức biểu thị số tiền mà người đó phải trả:

   T = số tiền đi 0,5 km đầu tiên + số tiền đi x – 0,5 km tiếp theo.

   + Bậc của đa thức là bậc của hạng tử có bậc cao nhất

   + Hệ số cao nhất là hệ số của hạng tử có bậc cao nhất

   + Hệ số tự do là hệ số của hạng tử bậc 0.

   b) Thay x = 9 vào đa thức, tìm giá trị của đa thức

   Lời giải:

   a) 0,5 km, người đó phải trả: 8 000 (đồng)

   Quãng đường còn lại người đó phải đi là: x – 0,5 (km)

   Trong x – 0,5 km đó, người đó phải trả: (x – 0,5). 11 000 ( đồng)

   Đa thức biểu thị số tiền mà người đó phải trả là:

   T(x) = 8 000 + (x – 0,5). 11 000

   = 8 000 + x . 11 000 – 0,5 . 11 000

   = 8 000 + 11 000 . x – 5 500

   = 11 000.x + 2 500

   Bậc của đa thức là: 1

   Hệ số cao nhất: 11 000

   Hệ số tự do: 2 500

   b) Thay x = 9 vào đa thức T(x), ta được:

   T(9) = 11 000 . 9 + 2 500 = 101 500

   Giá trị này nói lên số tiền mà người đó phải trả khi đi 9 km là 101 500 đồng

   Bài 7.43 trang 46 Toán lớp 7:  Cho đa thức bậc hai F(x) = ax² + bx + c, trong đó, a,b và c là những số với a $\ne$ 0

   a) Cho biết a + b + c = 0. Giải thích tại sao x = 1 là một nghiệm của F(x)

   b) Áp dụng, hãy tìm một nghiệm của đa thức bậc hai 2x² – 5x + 3

   Phương pháp giải:

   Giá trị x = m là 1 nghiệm của đa thức P(x) khi P(m) = 0

   Lời giải:

   a) Thay x = 1 vào đa thức F(x), ta có:

   F(1) = a.1² + b.1 + c = a+ b + c

   Mà a + b + c = 0

   Do đó, F(1) = 0. Như vậy x = 1 là một nghiệm của F(x)

   b) Ta có: Đa thức 2x² – 5x + 3 có a = 2 ; b = -5; c = 3 nên a + b + c = 2 + (-5) + 3 = 0

   Do đó, đa thức có 1 nghiệm là x = 1

   Bài 7.44 trang 46 Toán lớp 7: Cho đa thức A = x⁴ + x³ – 2x – 2

   a) Tìm đa thức B sao cho A + B = x³ + 3x + 1

   b) Tìm đa thức C sao cho A – C = x⁵

   c) Tìm đa thức D biết rằng D = (2x³ – 3) . A

   d) Tìm đa thức P sao cho A = (x+1) . P

   e) Có hay không một đa thức Q sao cho A = (x² + 1) . Q?

   Phương pháp giải:

   * Cách cộng (trừ) 2 đa thức:

   Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

   Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng ( trừ) theo từng cột.

   * Cách nhân 2 đa thức:

   Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

   Cách 2: Đặt tính nhân:

   + Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.

   + Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

   *  Muốn chia đa thức A cho đa thức B, ta làm như sau:

   Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

   Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1

   Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B

   Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3

   Bước 5: Làm tương tự như trên

   Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.

   Lời giải:

   a) Ta có:

   B = (A + B) – A

   = (x³ + 3x + 1) – (x⁴ + x³ – 2x – 2)

   = x³ + 3x + 1 – x⁴ – x³ + 2x + 2

   = – x⁴ + (x³ – x³) + (3x + 2x) + (1 + 2)

   = – x⁴ + 5x + 3

   b) C = (A – C) – A

   = x⁵ – (x⁴ + x³ – 2x – 2)

   = x⁵ – x⁴ –  x³ + 2x + 2)

   c) D = (2x³ – 3) . A

   = (2x³ – 3) . (x⁴ + x³ – 2x – 2)

   = 2x³ . (x⁴ + x³ – 2x – 2) + (-3) .(x⁴ + x³ – 2x – 2)

   = 2x³ . x⁴ + 2x³ . x³ + 2x³ . (-2x) + 2x³ . (-2) + (-3). x⁴ + (-3) . x³ + (-3). (-2x) + (-3). (-2)

   = 2x⁷ + 2x⁶ – 4x⁴ – 4x³ – 3x⁴ – 3x³ + 6x + 6

   = 2x⁷ + 2x⁶ + (-4x⁴ – 3x⁴) + (-4x³ – 3x³) + 6x + 6

   = 2x⁷ + 2x⁶ – 7x⁴ – 7x³ + 6x + 6

   d) P = A : (x+1) = (x⁴ + x³ – 2x – 2) : (x + 1)

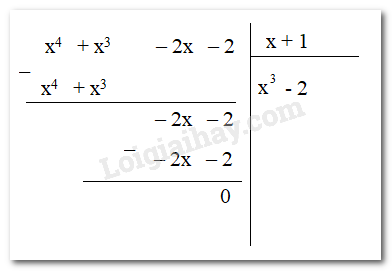   Vậy P = x³ – 2

   e) Q = A : (x² + 1)

   Nếu A chia cho đa thức x² + 1 không dư thì có một đa thức Q thỏa mãn

   Ta thực hiện phép chia (x⁴ + x³ – 2x – 2) : (x² + 1)

   

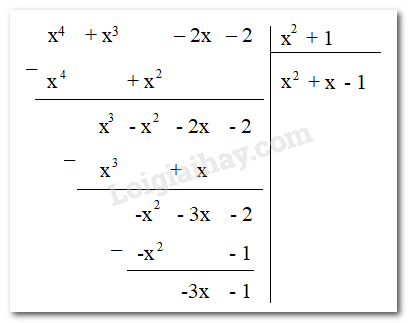
   Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn

   Bài 7.45 trang 46 Toán lớp 7: Cho đa thức P(x). Giải thích tại sao nếu có đa thức Q(x) sao cho P(x) = (x – 3) . Q(x) (tức là P(x) chia hết cho x – 3) thì x = 3 là một nghiệm của P(x)

   Phương pháp giải:

   Nghiệm của đa thức biến x là giá trị của x mà tại đó, đa thức có giá trị bằng 0.

   Lời giải:

   Vì tại x = 3 thì  P(x) = (3 – 3) . Q(x) = 0. Q(x) = 0 nên x = 3 là một nghiệm của đa thức P(x)

   Bài 7.46 trang 46 Toán lớp 7: Hai bạn Tròn và Vuông tranh luận với nhau như sau

   

   Hãy cho biết ý kiến của em và nêu một ví dụ minh họa.

   Phương pháp giải:

   Tổng của các đa thức là đa thức có bậc không lớn hơn bậc của các đa thức thành phần

   Lời giải:

   Tròn đúng, Vuông sai vì tổng của các đa thức là một đa thức có bậc không lớn hơn bậc của các đa thức thành phần

   Đa thức M(x) = x³ + 1 có thể viết được thành tổng của hai đa thức bậc 4 có hệ số cao nhất là 2 số đối nhau.

   Ví dụ:

   x³ + 1 = (x⁴ + 1) + (-x⁴ + x³)

   Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

   Luyện tập chung trang 44

   Bài 29: Làm quen với biến cố

   Bài 30: Làm quen với xác suất của biến cố

   Luyện tập chung trang 56