Với mỗi số nguyên dương, kí hiệu un=5.23n−2+33n−1 Một học sinh chứng minh un luôn chia hết cho 19 như sau: Bước 1: Khi n=1 ta có u1=5.21+32=19⇒u1⋮19 Bước 2: Giả sử uk=5.23k−2+33k+1  chia hết cho 19 với k≥1 Khi đó ta có uk+1=5.23k+1+33k+2=85.23k−2+33k−1+19.33k−1 Bước 3: Vì 5.23k−2+33k−1 và 19.33k−1 chia hết cho 19 nên uk+1  chia hết cho 19, Vậy un chia hết cho 19, ∀n∈ℕ* Lập luận trên đúng hay sai? Nếu sai thì bắt đầu từ bước nào?

Câu hỏi:

Với mỗi số nguyên dương, kí hiệu $u_n={5.2}^{3n-2}+3^{3n-1}$
Một học sinh chứng minh u_n luôn chia hết cho 19 như sau:
Bước 1: Khi n=1 ta có $u_1={5.2}^1+3^2=19\Rightarrow u_1⋮19$
Bước 2: Giả sử $u_k={5.2}^{3k-2}+3^{3k+1}$  chia hết cho 19 với $\mathrm{k}\ge 1$
Khi đó ta có $u_{k+1}={5.2}^{3k+1}+3^{3k+2}=8\left({5.2}^{3k-2}+3^{3k-1}\right)+{19.3}^{3k-1}$
Bước 3: Vì ${5.2}^{3k-2}+3^{3k-1} \mathrm{và} {19.3}^{3k-1}$ chia hết cho 19 nên ${\mathrm{u}}_{\mathrm{k}+1}$  chia hết cho 19,
Vậy u_n chia hết cho 19, $\forall n\in {\mathbb{N}}^{*}$
Lập luận trên đúng hay sai? Nếu sai thì bắt đầu từ bước nào?

A. Sai từ bước 1

B. Sai từ bước 3

C. Sai từ bước 2

D. Lập luận hoàn toàn đúng

Đáp án chính xác

Trả lời:

Chọn D
Lập luận hoàn toàn đúng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Chứng minh rằng với mọi số tự nhiên n≥2, ta luôn có 2n+1>2n+3        (*)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số tự nhiên $\mathrm{n}\ge 2$, ta luôn có $2^{n+1}>2n+3(*)$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Chứng minh rằng với mọi số nguyên dương n, ta có 1.4+2.7+…+n(3n+1)=nn+12        (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương n, ta có $1.4+2.7+\mathrm{\dots }+n(3n+1)=n{\left(n+1\right)}^2\left(1\right)$

   Trả lời:

   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Chứng minh rằng với mọi số nguyên dương n≥2 , ta có 1.22+2.33+3.44+…+n−1n2=nn2−13n+212      (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương $\mathrm{n}\ge 2$ , ta có ${1.2}^2+{2.3}^3+{3.4}^4+\mathrm{\dots }+\left(n-1\right)n^2=\frac{n\left(n^2-1\right)\left(3n+2\right)}{12}\left(1\right)$

   Trả lời:

   
   

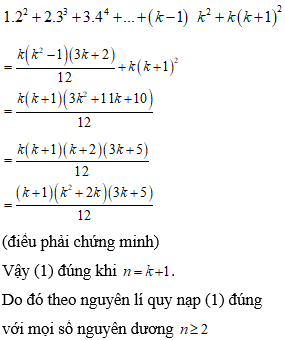
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Chứng minh rằng với mọi số nguyên dương n, ta có 11.2.3+12.3.4+…+1nn+1n+2=nn+34n+1n+2     (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương n, ta có $\frac{1}{\mathrm{1.2.3}}+\frac{1}{\mathrm{2.3.4}}+\mathrm{\dots }+\frac{1}{n\left(n+1\right)\left(n+2\right)}=\frac{n\left(n+3\right)}{4\left(n+1\right)\left(n+2\right)}\left(1\right)$

   Trả lời:

   
   

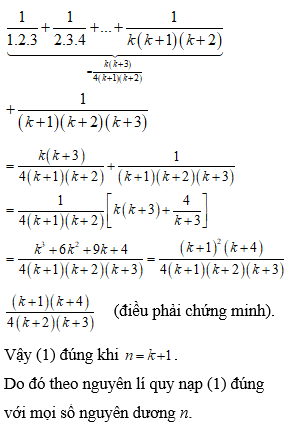
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Chứng minh rằng với mọi số nguyên dương n≥2  ta có 1n+1+1n+2+…+1n+n>1324     (1)
   
   

   Câu hỏi:
   

   Chứng minh rằng với mọi số nguyên dương $\mathrm{n}\ge 2$  ta có $\frac{1}{n+1}+\frac{1}{n+2}+\mathrm{\dots }+\frac{1}{n+n}>\frac{13}{24}\left(1\right)$

   Trả lời:

   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====