Hàm số y = sinxcos2x là:

Câu hỏi:

Hàm số y = sinxcos2x là:

A. Hàm chẵn.

B. Hàm không có tính chẵn, lẻ.

C. Hàm không có tính tuần hoàn.

D. Hàm lẻ.

Đáp án chính xác

Trả lời:

Chọn D
Tập xác định D = R
$\forall x\in D\Rightarrow – x\in D$
+ Cách 1:
Do y= sinx là hàm lẻ, y=cos2x là hàm chẵn nên hàm số y= sinx cos2x là hàm lẻ
+ Cách 2:  Ta có :  f(x) =  sin x. cos2x 
suy ra: f(- x) = sin(-x).  cos(-2 x) = – sinx. cos2x
Nên:  f(-x) = – f(x)
Do đó hàm số đã cho là hàm  số lẻ 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số y = 2sinxcosx + cos2x có giá trị lớn nhất là
   
   

   Câu hỏi:
   

   Hàm số $y = 2\sin x\cos x + \cos 2x$ có giá trị lớn nhất là

   A. 3

   B. $2\sqrt{2}$

   C. 2

   D. $\sqrt{2}$

   Đáp án chính xác

   Trả lời:

     

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Hàm số y = (sinx – cosx)2 + cos2x có giá trị nhỏ nhất là:
   
   

   Câu hỏi:
   

   Hàm số$y = {(\sin x – \cos x)}^2 + \cos 2x$ có giá trị nhỏ nhất là:

   A. -1

   B. $1–\sqrt{2}$

   Đáp án chính xác

   C. 0

   D. $1+\sqrt{2}$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số y = 2cos2x – 1 là hàm tuần hoàn với chu kì:
   
   

   Câu hỏi:
   

   Hàm số$y = 2{\cos }^{2}x – 1$ là hàm tuần hoàn với chu kì:

   A. T = π.

   Đáp án chính xác

   B. T = 2π.

   C. T = π2.

   D. T = π/2.

   Trả lời:

   Ta có y = 2cos2x – 1 = cos2x, do đó hàm số tuần hoàn với chu kì T = 2π/2 = π.Vậy đáp án là A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Hàm số y = sin(π/2-x) + cotx/3 là hàm tuần hoàn với chu kì:
   
   

   Câu hỏi:
   

   Hàm số $y = \sin (\pi /2–x) + cotx/3$ là hàm tuần hoàn với chu kì:

   A. T = π.

   B. T = 2π.

   C. T = 3π.

   D. T = 6π.

   Đáp án chính xác

   Trả lời:

   Hàm số $y_1=\sin \left(\frac{\pi }{2}-x\right)$ có chu kì $T_1=\frac{2\pi }{\left|-1\right|}=2\pi$Hàm số $y_2=\cot \left(\frac{x}{3}\right)$ có chu kì $T_2=\frac{\pi }{\left|\frac{1}{3}\right|}=3\pi$Suy ra hàm số đã cho $y=y_1+y_2$ có chu kì $T=BCNN\left(2,3\right)\pi =6\pi$.Vậy đáp án là D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hình vẽ bên là một phần đồ thị của hàm số nào sau đây?
   
   

   Câu hỏi:
   

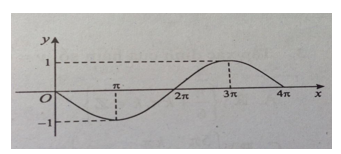   Hình vẽ bên là một phần đồ thị của hàm số nào sau đây?

   A. y = sinx/2

   B. y = cosx/2

   C. y = – cosx/4

   D. y = sin( – x/2)

   Đáp án chính xác

   Trả lời:

   Đồ thị hàm số đi qua gốc tọa độ nên loại ngay các phương án B và C. Đồ thị hàm số đi qua (π; -1) nên phương án A cũng không thỏa mãn.Vậy đáp án là D.Nhận xét: Từ đồ thị ta nhận thấy hàm số có chu kì T =4π nên ta có thể loại ngay phương án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====