Cho tứ diện ABCD, gọi  (M không trùng với A, B). N và K lần lượt là trung điểm BC, CD. Giao tuyến của (ABD) và (MNK) là

Câu hỏi:

Cho tứ diện ABCD, gọi  (M không trùng với A, B). N và K lần lượt là trung điểm BC, CD. Giao tuyến của (ABD) và (MNK) là

A. MN

B. MD

C. MC

D. Mx song song với BD và NK

Đáp án chính xác

Trả lời:

Đáp án D

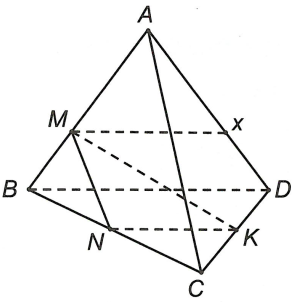
Ta có $M\in \left(ABD\right)\cap \left(MNK\right)$ và CD // NK
Nên $\left(ABD\right)\cap \left(MNK\right)=Mx$sao cho Mx // DB // NK

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

   Trả lời:

   

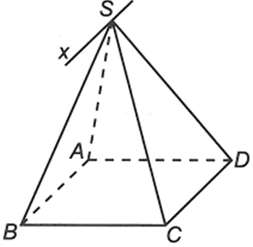
   Ta có $\left\{\begin{array}{l}\left(SAB\right)\cap \left(SCD\right)=S\\ AB\subset \left(SAB\right),CD\subset \left(SCD\right)\\ AB/\text{}/CD\end{array}\right.$
   Suy ra $\left(SAB\right)\cap \left(SCD\right)=Sx$ với $Sx/\text{}/AB/\text{}/CD$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng: a) SAB∩SCD
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), đáy lớn AB. Cho M là điểm bất kì thuộc cạnh SC. Tìm giao tuyến của các mặt phẳng:
   a) $\left(SAB\right)\cap \left(SCD\right)$

   Trả lời:

   

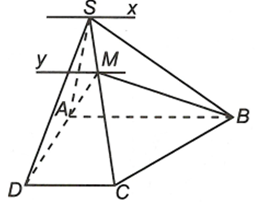
   a) Ta có $\left(SAB\right)\cap \left(SCD\right)=S$, mà AB // CD
   Suy ra $\left(SAB\right)\cap \left(SCD\right)=Sx$, trong đó $Sx/\text{}/AB/\text{}/CD$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) SCD∩MAB
   
   

   Câu hỏi:
   

   b) $\left(SCD\right)\cap \left(MAB\right)$

   Trả lời:

   b) Do $M\in SC$ nên $\left(SCD\right)\cap \left(MAB\right)=M$, mặt khác AB // CD
   $\Rightarrow \left(SCD\right)\cap \left(MAB\right)=My$, trong đó My // AB // CD

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC)
   
   

   Câu hỏi:
   

   Cho tứ diện SABC. Gọi G, I lần lượt là trọng tâm của tam giác ABC và SAB. Tìm giao tuyến của mặt phẳng (AIG) và mặt phẳng (SAC)

   Trả lời:

   

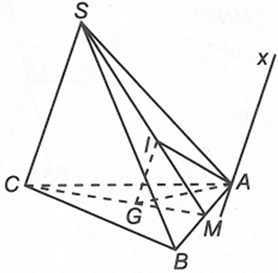
   Gọi M là trung điểm của AB.
   Do I là trọng tâm của tam giác SAB suy ra $\frac{MI}{MS}=\frac{1}{3}$
   Tương tự ta có $\frac{MG}{MC}=\frac{1}{3}$
   Suy ra $\frac{MI}{MS}=\frac{MG}{MB}\Rightarrow GI/\text{}/SC$
   Từ đó ta có $\left(SAC\right)\cap \left(AIG\right)=Ax$, trong đó Ax // SC // GI

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
   a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAC) và (SBD)

   Trả lời:

   

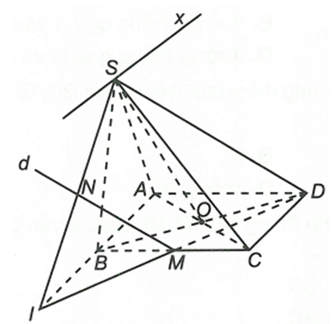
   a) Ta có $\left\{\begin{array}{l}S\in \left(SAB\right)\cap \left(SCD\right)\\ AB\subset \left(SAB\right);CD\subset \left(SCD\right)\\ AB/\text{}/CD\end{array}\right.$
   $\Rightarrow \left(SAB\right)\cap \left(SCD\right)=Sx$ trong đó Sx // AB // CD
   Trong (ABCD) gọi $\left\{O\right\}=AC\cap BD$, suy ra $O\in \left(SAC\right)\cap \left(SBD\right) \left(1\right)$
   Lại có $S\in \left(SAC\right)\cap \left(SBD\right) \left(2\right)$
   Từ (1) và (2), suy ra $SO=\left(SAC\right)\cap \left(SBD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====