Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. Tìm thiết diện tạo bởi (CU) và hình chóp

Câu hỏi:

Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD sao cho BD và IJ không song song. Tìm thiết diện tạo bởi (CU) và hình chóp

Trả lời:

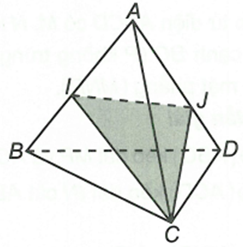
Ta có
$\left(CIJ\right)\cap \left(ABD\right)=IJ\left(CIJ\right)\cap \left(ABC\right)=IC\left(CIJ\right)\cap \left(ACD\right)=CJ$

Vậy thiết diện cần tìm là ∆CIJ

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC. a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SB và SC.
   a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

   Trả lời:

   

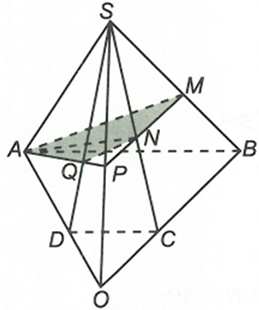
   a) Trong mặt phẳng (ABCD): $\left\{O\right\}=AD\cap BC$
   Ta có (SAD) và (SBC) có S chung
   Lại có $\left\{\begin{array}{l}O\in AD\subset \left(SAD\right)\Rightarrow O\in \left(SAD\right)\\ O\in BC\subset \left(SBC\right)\Rightarrow O\in \left(SBC\right)\end{array}\right.\Rightarrow O\in \left(SAD\right)\cap \left(SBC\right)$
   Nên $SO=\left(SAD\right)\cap \left(SBC\right)$

    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) Tìm thiết diện của hình chóp với mặt phẳng (AMN)
   
   

   Câu hỏi:
   

   b) Tìm thiết diện của hình chóp với mặt phẳng (AMN)

   Trả lời:

   b) Trong mặt phẳng (SOB) có $\left\{P\right\}=SO\cap MN$ và trong (SOA) gọi $\left\{Q\right\}=AP\cap SD$
   Khi đó ta có
   $\begin{array}{l}\left(SBC\right)\cap \left(AMN\right)=MN\\ \left(SCD\right)\cap \left(AMN\right)=QN\\ \left(SAD\right)\cap \left(AMN\right)=AQ\\ \left(SAB\right)\cap \left(AMN\right)=AM\end{array}$

   Vậy thiết diện của tứ diện cắt bởi mặt phẳng (AMN) là tứ giác AMNQ

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).

   Trả lời:

   

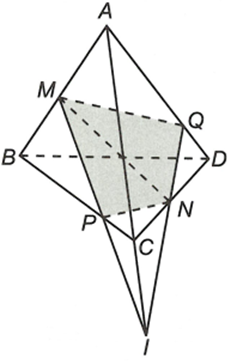
   Trong mp (ABC) kéo dài MP và AC cắt nhau tại I.
   Trong mp (ACD) kéo dài IN cắt AD tại Q
   Ta có
   $\begin{array}{l}\left(ABC\right)\cap \left(MNP\right)=MP\\ \left(BCD\right)\cap \left(MNP\right)=PN\\ \left(ACD\right)\cap \left(MNP\right)=NQ\\ \left(ABD\right)\cap \left(MNP\right)=QM\end{array}$
   Vậy thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNPQ

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt trên các cạnh CB, CD, SA. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (MNP)

   Trả lời:

   

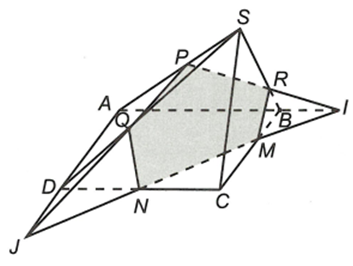
    Trong mặt phẳng (ABCD) gọi $\left\{I\right\}=MN\cap AB;\left\{J\right\}=MN\cap AD$
   Trong (SAD) gọi $\left\{Q\right\}=SD\cap PJ$
   Trong (SAB) gọi $\left\{R\right\}=SB\cap PI$
   Khi đó, dễ dàng chứng minh được M, N, Q, P, R lần lượt là giao điểm của (MNP) với các cạnh BC, CD, SD, SA, SB.
   Do đó thiết diện cần tìm là ngũ giác MNQPR

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD (AB và CD không song song) và M là điểm nằm trong ∆SCD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (ABM)

   Trả lời:

   

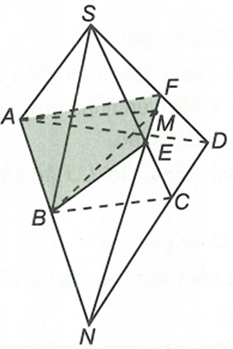
   Trong (ABCD) gọi $\left\{N\right\}=AB\cap CD$
   Trong (SCD) gọi $\left\{E\right\}=MN\cap SC;\left\{F\right\}=MN\cap SD$
   Khi đó, dễ dàng chứng minh được E, F lần lượt là giao điểm của (ABM) với SC, SD.
   Do đó thiết diện cần tìm là tứ giác ABEF.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====