Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Chọn khẳng định đúng trong các khẳng định sau.

Câu hỏi:

Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Chọn khẳng định đúng trong các khẳng định sau.

A. $IJ\text{ // }\left(SAD\right).$

B. $IJ\text{ // }\left(ABD\right).$

Đáp án chính xác

C. $IJ\text{ // }\left(SAB\right).$

D. $IJ\text{ // }\left(SDB\right).$

Trả lời:

Đáp án B

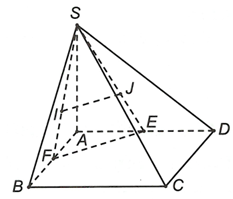
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Chọn khẳng định đúng trong các khẳng định sau.

Vì I; J lần lượt là trọng tâm các tam giác SAD và SAB nên $\frac{SI}{SE}=\frac{SJ}{SF}=\frac{2}{3}\Rightarrow IJ\text{ // }EF.$
Do $EF\subset \left(ABD\right)$ nên IJ // (ABD)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Chứng minh AB // (SCD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Chứng minh AB // (SCD)

   Trả lời:

   
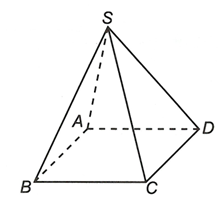
   Ta có AB // CD mà $CD\subset \left(SCD\right)\Rightarrow AB\text{ // }\left(SCD\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tứ diện ABCD, gọi M là trung điểm của CD, E là trung điểm của AM và F là trung điểm của BM.a) Chứng minh rằng EF song song với các mặt phẳng (ABC) và (ABD)
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD, gọi M là trung điểm của CD, E là trung điểm của AM và F là trung điểm của BM.
   a) Chứng minh rằng EF song song với các mặt phẳng (ABC) và (ABD)

   Trả lời:

   

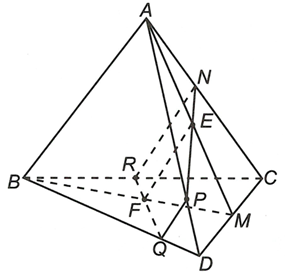
   a) Ta có EF là đường trung bình của tam giác ABM suy ra  
   Do $AB\subset \left(ABC\right)$ nên $EF\text{ // }\left(ABC\right)$ và $AB\subset \left(ABD\right)$ nên  $EF\text{ // }\left(ABD\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) Lấy điểm N trên cạnh AC. Xác định thiết diện của hình chóp với mặt phẳng (NEF). Thiết diện là hình gì?
   
   

   Câu hỏi:
   

   b) Lấy điểm N trên cạnh AC. Xác định thiết diện của hình chóp với mặt phẳng (NEF). Thiết diện là hình gì?

   Trả lời:

   b) Kéo dài NE cắt AD tại P.
   Do EF // (ABD) nên kẻ Px // AB và cắt BD tại Q.
   Kẻ QF cắt BC tại R.
   Khi đó hình thang NPQR là thiết diện của mặt phẳng (NEF) với tứ diện ABCD.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tứ diện ABCD, G là trọng tâm ΔABD và M là điểm trên cạnh BC sao cho MB = 2MC. Chứng minh đường thẳng MG song song với mặt phẳng (ACD)
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD, G là trọng tâm $\mathrm{\Delta ABD}$ và M là điểm trên cạnh BC sao cho MB = 2MC. Chứng minh đường thẳng MG song song với mặt phẳng (ACD)

   Trả lời:

   

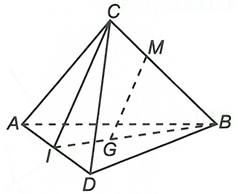
   Gọi I là trung điểm của AD.
   Ta có G là trọng tâm $\Delta ABD$ khi đó $\frac{BG}{BI}=\frac{2}{3}.$
   Mặt khác, $M\in BC$ và $BM=2MC\Rightarrow \frac{BM}{BC}=\frac{2}{3}.$
   Từ đó suy ra $\frac{BG}{BI}=\frac{BM}{BC}.$
   Áp dụng định lý Ta-lét đảo suy ra $GM\text{ // }CI.$  
   Mà $CI\subset \left(ACD\right)$ nên $GM\text{ // }\left(ACD\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Chứng minh đường thẳng OI song song với mặt phẳng (SAB) và mặt phẳng (SAD)
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Chứng minh đường thẳng OI song song với mặt phẳng (SAB) và mặt phẳng (SAD)

   Trả lời:

   

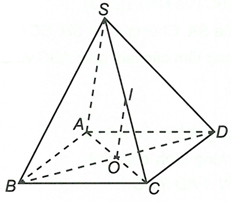
   Ta có IO là đường trung bình của tam giác SAC suy ra IO // SA
   Do $SA\subset \left(SAB\right)$ và $SA\subset \left(SAD\right)$ từ đó suy ra $IO\text{ // }\left(SAB\right)$và $IO\text{ // }\left(SAD\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====