Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC. a) Tìm giao điểm I của AM với (SBD). Chứng minh IA = 2.IM

Câu hỏi:

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm giao điểm I của AM với (SBD). Chứng minh IA = 2.IM

Trả lời:

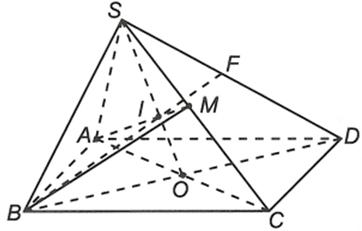
a) Trong mặt phẳng (ABCD) gọi $AC\cap BD=\left\{O\right\}$
Ta có $AM\subset \left(SAC\right)$; (SAC) và (SBD) có S chung
Lại có $\left\{\begin{array}{l}O\in AC\subset \left(SAC\right)\Rightarrow O\in \left(SAC\right)\\ O\in BD\subset \left(SBD\right)\Rightarrow O\in \left(SBD\right)\end{array}\right.\Rightarrow O\in \left(SAC\right)\cap \left(SBD\right)$
Nên $SO=\left(SAC\right)\cap \left(SBD\right)$
Trong mặt phẳng $\left(SAC\right):\left\{I\right\}=AM\cap SO$
Vậy $AM\cap \left(SBD\right)=\left\{I\right\}$
Xét ∆SAC có AM, SO là hai đường trung tuyến nên I là trọng tâm ∆SAC, suy ra theo tính chất trọng tâm ta có AI = 2IM

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD với I là trung điểm AB và AJ=23AD . Tìm giao điểm của IJ và (BCD)
   
   

   Câu hỏi:
   

   Cho tứ diện ABCD. Gọi I, J lần lượt là các điểm nằm trên AB, AD với I là trung điểm AB và $AJ=\frac{2}{3}AD$ . Tìm giao điểm của IJ và (BCD)

   Trả lời:

   

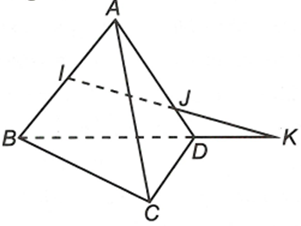
   Trong tam giác ∆ABC có:
   $\left\{\begin{array}{l}\frac{AI}{AB}=\frac{1}{2}\\ \frac{AJ}{AD}=\frac{2}{3}\end{array}\right.\Rightarrow \frac{AI}{AB}\ne \frac{AJ}{AD}$
   Do đó IJ và BD không song song theo định lý Ta-lét.
   Ta có $IJ\subset \left(ABD\right)$

   Lại có $\left(ABD\right)\cap \left(BCD\right)=BD$
   Trong mặt phẳng (ABD) gọi $\left\{K\right\}=IJ\cap BD$
   Vậy $IJ\cap \left(BCD\right)=\left\{K\right\}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác BCD và điểm A không thuộc (BCD). Gọi K là trung điểm của AD và G là trọng tâm tam giác ABC. Tìm giao điểm của đường thẳng GK và (BCD)
   
   

   Câu hỏi:
   

   Cho tam giác BCD và điểm A không thuộc (BCD). Gọi K là trung điểm của AD và G là trọng tâm tam giác ABC. Tìm giao điểm của đường thẳng GK và (BCD)

   Trả lời:

   

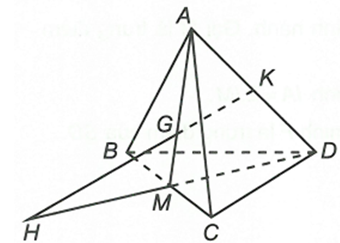
   Trong tam giác ∆AMD có $\left\{\begin{array}{l}\frac{AG}{AM}=\frac{2}{3}\\ \frac{AK}{AD}=\frac{1}{2}\end{array}\right.\Rightarrow \frac{AG}{AM}\ne \frac{AK}{AD}$
   Nên GK và MD không song song theo định lý Ta-lét.
   Ta có: $GK\subset \left(AMD\right)$ và $\left(AMD\right)\cap \left(BCD\right)=MD$, suy ra trong $\left(AMD\right):\left\{H\right\}=MD\cap GK$
   Vậy $GK\cap \left(BCD\right)=\left\{H\right\}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm AC, BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD. a) Tìm giao điểm của CD và (MNP)
   
   

   Câu hỏi:
   

   Cho bốn điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm AC, BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
   a) Tìm giao điểm của CD và (MNP)

   Trả lời:

   

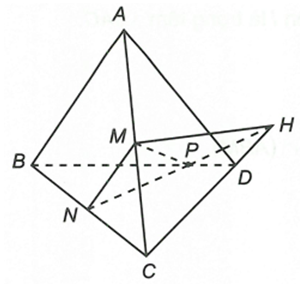
   a) Trong ∆BCD có $\left\{\begin{array}{l}\frac{BN}{NC}=1\\ \frac{BP}{PD}=2\end{array}\right.\Rightarrow \frac{BN}{NC}\ne \frac{BP}{PD}$
   Do đó NP và CD không song song theo định lý Ta-lét.
   Ta có $CD\subset \left(BCD\right)$ và $\left(BCD\right)\cap \left(MNP\right)=NP$
   Trong $\left(BCD\right):CD\cap NP=\left\{H\right\}$
   Vậy $CD\cap \left(MNP\right)=\left\{H\right\}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD)
   
   

   Câu hỏi:
   

   b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD)

   Trả lời:

   b) Xét hai mặt phẳng (MNP) và (ACD) có $M\in \left(MNP\right)\cap \left(ACD\right)\left(1\right)$
   Lại có $\left\{\begin{array}{l}H\in NP\subset \left(MNP\right)\Rightarrow H\in \left(MNP\right)\\ H\in CD\subset \left(ACD\right)\Rightarrow H\in \left(ACD\right)\end{array}\right.\Rightarrow H\in \left(MNP\right)\cap \left(ACD\right) \left(2\right)$
   Từ (1) và (2) suy ra $MH=\left(MNP\right)\cap \left(ACD\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) Tìm giao điểm F của SD với (ABM). Chứng minh F là trung điểm của SD.
   
   

   Câu hỏi:
   

   b) Tìm giao điểm F của SD với (ABM). Chứng minh F là trung điểm của SD.

   Trả lời:

   b) Ta có (SBD) và (ABM) có B chung
   Lại có $\left\{\begin{array}{l}I\in SO\subset \left(SBD\right)\Rightarrow I\in \left(SBD\right)\\ I\in AM\subset \left(ABM\right)\Rightarrow I\in \left(ABM\right)\end{array}\right.\Rightarrow I\in \left(SBD\right)\cap \left(ABM\right)$
   Nên $BI=\left(SBD\right)\cap \left(ABM\right)$
   Trong mặt phẳng $\left(SBD\right):\left\{F\right\}=BI\cap SD$
   Vậy $\left\{F\right\}\in \left(ABM\right)\cap \left(SBD\right)$
   Xét ∆SBD có SI = 2.OI và O là trung điểm BD nên I là trọng tâm ∆SBD.
   Suy ra BF là trung tuyến ∆SBD
   Vậy F là trung điểm SD.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====