Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 1) và B(7; 5). Tìm toạ độ của điểm C thuộc trục hoành sao cho C cách đều A và B.

Câu hỏi:

Trong mặt phẳng toạ độ Oxy cho hai điểm A(1; 1) và B(7; 5).
Tìm toạ độ của điểm C thuộc trục hoành sao cho C cách đều A và B.

Trả lời:

Lời giải
Vì C cách đều A và B nên CA = CB
AC² = BC²
Giả sử C(x; 0) là điểm thuộc trục hoành
Với A(1; 1); B(7; 5) và C(x; 0) ta có:
• \(\overrightarrow {AC} = \left( {x – 1; – 1} \right)\) AC² = (x – 1)² + (–1)²
AC² = x² – 2x + 2
• \(\overrightarrow {BC} = \left( {x – 7; – 5} \right)\) BC² = (x – 7)² + (–5)²
BC² = x² – 14x + 74
Do đó AC² = BC²
x² – 2x + 2 = x² – 14x + 74
12x = 72
x = 6
Vậy C(6; 0).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác đều ABC có độ dài các cạnh bằng 1. Gọi M là trung điểm của BC. Tính tích vô hướng của các cặp vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {BA} ,\) \(\overrightarrow {MA} \) và \(\overrightarrow {AC} .\)
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC có độ dài các cạnh bằng 1.
   Gọi M là trung điểm của BC. Tính tích vô hướng của các cặp vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {BA} ,\) \(\overrightarrow {MA} \) và \(\overrightarrow {AC} .\)

   Trả lời:

   Lời giải
   
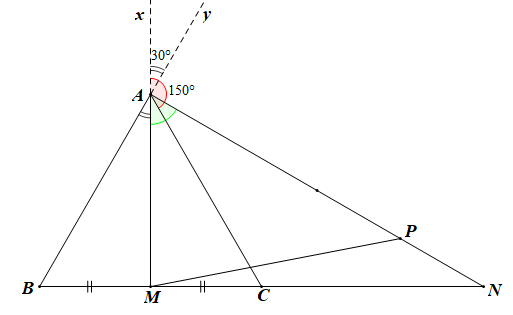
   Tam giác ABC đều có M là trung điểm của BC nên đường trung tuyến AM đồng thời là đường phân giác và đường cao.
   \( \Rightarrow \widehat {BAM} = \widehat {MAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.60^\circ = 30^\circ \)
   Gọi Ax là tia đối của tia AM, tia Ay là tia đối của tia AB.
   Do đó \(\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right) = \widehat {xAy} = \widehat {BAM} = 30^\circ \)
   \(\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = \widehat {xAC} = 180^\circ – \widehat {MAC}\)
   \( \Rightarrow \left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = 180^\circ – 30^\circ = 150^\circ \)
   Khi đó ta có:
   • \(\overrightarrow {MA} .\overrightarrow {BA} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {BA} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right)\)
   \( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = MA.BA.c{\rm{os30}}^\circ \)
   Xét tam giác BAM vuông tại M, theo định lí Pythagoras ta có:
   \(MA = \sqrt {B{A^2} – B{M^2}} = \sqrt {{1^2} – {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
   \( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = \frac{{\sqrt 3 }}{2}.1.\frac{{\sqrt 3 }}{2} = \frac{3}{4}.\)
   • \(\overrightarrow {MA} .\overrightarrow {AC} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {AC} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right)\)
   \( \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = MA.AC.c{\rm{os150}}^\circ \)
   \( \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}.1.\frac{{ – \sqrt 3 }}{2} = \frac{{ – 3}}{4}.\)
   Vậy \(\overrightarrow {MA} .\overrightarrow {BA} = \frac{3}{4}\) và \(\overrightarrow {MA} .\overrightarrow {AC} = \frac{{ – 3}}{4}.\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác đều ABC có độ dài các cạnh bằng 1. Gọi N là điểm đối xứng với B qua C. Tính tích vô hướng \(\overrightarrow {AM} .\overrightarrow {AN} .\)
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC có độ dài các cạnh bằng 1.
   Gọi N là điểm đối xứng với B qua C. Tính tích vô hướng \(\overrightarrow {AM} .\overrightarrow {AN} .\)

   Trả lời:

   Lời giải
   
   • Vì M là trung điểm của BC nên
   \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
   \( \Rightarrow \overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
   • N đối xứng với B qua C nên C là trung điểm của BN
   \( \Rightarrow \overrightarrow {AB} + \overrightarrow {AN} = 2\overrightarrow {AC} \)\( \Rightarrow \overrightarrow {AN} = 2\overrightarrow {AC} – \overrightarrow {AB} \)
   Khi đó \(\overrightarrow {AM} .\overrightarrow {AN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {2\overrightarrow {AC} – \overrightarrow {AB} } \right)\)
   \( = \frac{1}{2}.\left( {2\overrightarrow {AB} .\overrightarrow {AC} – \overrightarrow {AB} .\overrightarrow {AB} + 2\overrightarrow {AC} .\overrightarrow {AC} – \overrightarrow {AC} .\overrightarrow {AB} } \right)\)
   \( = \frac{1}{2}.\left( {2{{\overrightarrow {AC} }^2} – {{\overrightarrow {AB} }^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\)
   \( = \frac{1}{2}.\left( {2{{\left| {\overrightarrow {AC} } \right|}^2} – {{\left| {\overrightarrow {AB} } \right|}^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\)
   Mà \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.cos\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\)
   \( = AB.AC.cos\widehat {BAC} = 1.1.\cos 60^\circ = \frac{1}{2}.\)
   Do đó \(\overrightarrow {AM} .\overrightarrow {AN} \)\( = \frac{1}{2}.\left( {2A{C^2} – A{B^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\)
   \( = \frac{1}{2}.\left( {{{2.1}^2} – {1^2} + \frac{1}{2}} \right)\)
   \( = \frac{1}{2}.\frac{3}{2} = \frac{3}{4}.\)
   Vậy \(\overrightarrow {AM} .\overrightarrow {AN} = \frac{3}{4}\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác đều ABC có độ dài các cạnh bằng 1. Lấy điểm P thuộc đoạn AN sao cho AP = 3PN. Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} .\) Tính độ dài đoạn MP.
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC có độ dài các cạnh bằng 1.
   Lấy điểm P thuộc đoạn AN sao cho AP = 3PN. Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} .\) Tính độ dài đoạn MP.

   Trả lời:

   Lời giải
   
   • Vì P thuộc đoạn thẳng AN thỏa mãn AP = 3PN \( \Rightarrow AP = \frac{3}{4}AN\)
   \( \Rightarrow \overrightarrow {AP} = \frac{3}{4}\overrightarrow {AN} = \frac{3}{4}.\left( {2\overrightarrow {AC} – \overrightarrow {AB} } \right)\)
   \( \Rightarrow \overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} – \frac{3}{4}\overrightarrow {AB} \)
   • Ta có: \(\overrightarrow {MP} = \overrightarrow {AP} – \overrightarrow {AM} \)
   \( = \left( {\frac{3}{2}\overrightarrow {AC} – \frac{3}{4}\overrightarrow {AB} } \right) – \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
   \( = \frac{3}{2}\overrightarrow {AC} – \frac{3}{4}\overrightarrow {AB} – \frac{1}{2}\overrightarrow {AB} – \frac{1}{2}\overrightarrow {AC} \)
   \( = \left( {\frac{3}{2}\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AC} } \right) – \left( {\frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} } \right)\)
   \( = \overrightarrow {AC} – \frac{5}{4}\overrightarrow {AB} \)
   \( \Rightarrow MP = \left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {AC} – \frac{5}{4}\overrightarrow {AB} } \right|\)
   \( \Rightarrow M{P^2} = {\left( {\overrightarrow {AC} – \frac{5}{4}\overrightarrow {AB} } \right)^2}\)
   \( = {\overrightarrow {AC} ^2} – 2.\frac{5}{4}\overrightarrow {AC} .\overrightarrow {AB} + \frac{{25}}{{16}}{\overrightarrow {AB} ^2}\)
   \( = A{C^2} + \frac{{25}}{{16}}A{B^2} – \frac{5}{2}\overrightarrow {AC} .\overrightarrow {AB} \)
   \( = {1^2} + \frac{{25}}{{16}}{.1^2} – \frac{5}{2}.\frac{1}{2}\)
   \( = \frac{{21}}{{16}}\)
   \( \Rightarrow MP = \sqrt {\frac{{21}}{{16}}} = \frac{{\sqrt {21} }}{4}.\)
   Vậy \(\overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} – \frac{3}{4}\overrightarrow {AB} ;\)\(\overrightarrow {MP} = \overrightarrow {AC} – \frac{5}{4}\overrightarrow {AB} \) và \(MP = \frac{{\sqrt {21} }}{4}.\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chữ nhật ABCD có AB = 1, \(BC = \sqrt 2 .\) Gọi M là trung điểm của AD. Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD có AB = 1, \(BC = \sqrt 2 .\) Gọi M là trung điểm của AD.
   Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.

   Trả lời:

   Lời giải
   
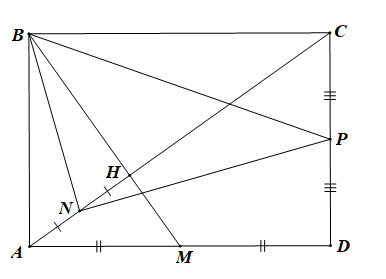
   a) Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \) khi đó \(\left| {\overrightarrow a } \right| = 1\)và \(\left| {\overrightarrow b } \right| = \sqrt 2 .\)
   Vì AB ⊥ AD nên \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \)
   ABCD là hình chữ nhật nên cũng là hình bình hành nên ta có:
   \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow a + \overrightarrow b \) (quy tắc hình bình hành)
   M là trung điểm của AD nên \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AD} = \frac{1}{2}\overrightarrow b \)
   Suy ra \(\overrightarrow {BM} = \overrightarrow {AM} – \overrightarrow {AB} = \frac{1}{2}\overrightarrow b – \overrightarrow a \)
   Khi đó \(\overrightarrow {AC} .\overrightarrow {BM} = \left( {\overrightarrow a + \overrightarrow b } \right).\left( {\frac{1}{2}\overrightarrow b – \overrightarrow a } \right)\)
   \( = \frac{1}{2}\overrightarrow a .\overrightarrow b – \overrightarrow a .\overrightarrow a + \frac{1}{2}\overrightarrow b .\overrightarrow b – \overrightarrow a .\overrightarrow b \)
   \( = \frac{1}{2}\overrightarrow 0 – {\overrightarrow a ^2} + \frac{1}{2}{\overrightarrow b ^2} – \overrightarrow 0 \) (do \(\overrightarrow a .\overrightarrow b = \overrightarrow 0 \))
   \( = – {\left| {\overrightarrow a } \right|^2} + \frac{1}{2}{\left| {\overrightarrow b } \right|^2}\)
   \( = – {1^2} + \frac{1}{2}.{\left( {\sqrt 2 } \right)^2} = 0\)
   Do đó \(\overrightarrow {AC} .\overrightarrow {BM} = 0 \Leftrightarrow \overrightarrow {AC} \bot \overrightarrow {BM} \)
   AC ⊥ BM.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chữ nhật ABCD có AB = 1, \(BC = \sqrt 2 .\) Gọi M là trung điểm của AD. Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằng tam giác NBP là một tam giác vuông.
   
   

   Câu hỏi:
   

   Cho hình chữ nhật ABCD có AB = 1, \(BC = \sqrt 2 .\) Gọi M là trung điểm của AD.
   Gọi H là giao điểm của AC, BM. Gọi N là trung điểm của AH và P là trung điểm của CD. Chứng minh rằng tam giác NBP là một tam giác vuông.

   Trả lời:

   Lời giải
   
   • Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:
   AC² = AB² + BC² = 1 + \({\left( {\sqrt 2 } \right)^2}\)= 3
   \( \Rightarrow AC = \sqrt 3 \)
   Theo hệ thức lượng trong tam giác vuông ta có:
   AB² = AH.AC \( \Rightarrow AH = \frac{{A{B^2}}}{{AC}} = \frac{{{1^2}}}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
   \( \Rightarrow \frac{{AH}}{{AC}} = \frac{{\sqrt 3 }}{3}:\sqrt 3 = \frac{1}{3}\)
   \( \Rightarrow \overrightarrow {AH} = \frac{1}{3}\overrightarrow {AC} \)
   Khi đó \(\overrightarrow {HC} = \frac{2}{3}\overrightarrow {AC} \) và \(\overrightarrow {HA} = – \frac{1}{3}\overrightarrow {AC} \)
   Ta có \(\overrightarrow {NB} = \overrightarrow {NA} + \overrightarrow {AB} \) (quy tắc ba điiểm)
   Vì N là trung điểm của AH nên \(\overrightarrow {NA} = \frac{1}{2}\overrightarrow {HA} \)
   \( \Rightarrow \overrightarrow {NB} = \frac{1}{2}.\left( { – \frac{1}{3}\overrightarrow {AC} } \right) + \overrightarrow {AB} \)
   \( = – \frac{1}{6}.\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow a \)
   \( = \frac{5}{6}\overrightarrow a – \frac{1}{6}\overrightarrow b \)
   • Có N là trung điểm của HA và P là trung điểm của CD, theo kết quả bài 4.12, trang 58, Sách giáo khoa Toán 10, tập một, ta có:
   \(\overrightarrow {AD} + \overrightarrow {HC} = 2\overrightarrow {NP} \)\( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {HC} } \right)\)
   \( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {HC} \)
   \( = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}.\frac{2}{3}\overrightarrow {AC} \)
   \( = \frac{1}{2}\overrightarrow b + \frac{1}{3}.\left( {\overrightarrow a + \overrightarrow b } \right)\)
   \( = \frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b \)
   Khi đó \(\overrightarrow {NB} .\overrightarrow {NP} = \left( {\frac{5}{6}\overrightarrow a – \frac{1}{6}\overrightarrow b } \right).\left( {\frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b } \right)\)
   \( = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b – \frac{1}{{18}}\overrightarrow a .\overrightarrow b – \frac{5}{{36}}{\overrightarrow b ^2}\)
   \( = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b – \frac{1}{{18}}\overrightarrow a .\overrightarrow b – \frac{5}{{36}}{\overrightarrow b ^2}\)
   \( = \frac{5}{{18}}{\left| {\overrightarrow a } \right|^2} + \frac{{25}}{{36}}\overrightarrow 0 – \frac{1}{{18}}\overrightarrow 0 – \frac{5}{{36}}{\left| {\overrightarrow b } \right|^2}\) (do \(\overrightarrow a .\overrightarrow b = \overrightarrow 0 \))
   \( = \frac{5}{{18}}{.1^2} – \frac{5}{{36}}.{\left( {\sqrt 2 } \right)^2}\)
   \( = \frac{5}{{18}} – \frac{5}{{36}}.2 = 0\)
   Do đó \(\overrightarrow {NB} .\overrightarrow {NP} = 0 \Rightarrow \overrightarrow {NB} \bot \overrightarrow {NP} \)
   NB ⊥ NP.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====