Câu hỏi:
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
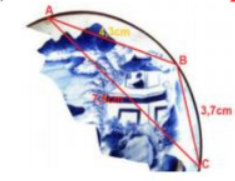
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
A. 5,73 cm;
Đáp án chính xác
B. 6,01 cm;
C. 5,85 cm;
D. 4,57 cm.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Nửa chu vi của tam giác ABC là:
Diện tích tam giác ABC theo công thức Heron là:
Mặt khác:
Vậy bán kính của chiếc đĩa là khoảng 5,73 cm.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
Phát biểu nào dưới đây là sai.
Câu hỏi:
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
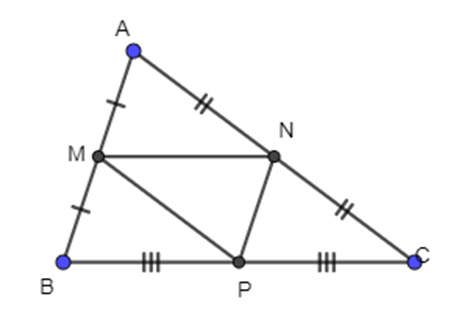
Phát biểu nào dưới đây là sai.
A. \(\overrightarrow {MN} = \overrightarrow {PC} \);
B. \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \);
C. \(\overrightarrow {MB} = \overrightarrow {AM} \);
D. \(\overrightarrow {MN} = \overrightarrow {PB} \).
Đáp án chính xác
Trả lời:
Đáp án đúng là D
+) Xét tam giác ABC, có:
M là trung điểm AB
N là trung điểm của AC
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC và MN = \(\frac{1}{2}\)BC
Mà BP = PC = \(\frac{1}{2}\)BC (P là trung điểm của BC)
⇒ MN = CP = PB (1)
Vì MN // BC nên MN // CP. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng phương. Suy ra \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng hướng (2)
Từ (1) và (2) suy ra \(\overrightarrow {MN} \) = \(\overrightarrow {CP} \). Do đó đáp án A đúng.
Tương tự MN //BC hay MN // PB. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PB} \) cùng phương nhưng ngược hướng (3)
Từ (1) và (3) suy ra \(\overrightarrow {MN} \) không bằng \(\overrightarrow {PB} \). Do đó đáp án D sai.
+) Ta có \(\overrightarrow {AA} \) và \(\overrightarrow {PP} \) là các vectơ – không.
Mà mọi vectơ – không có cùng độ dài và cùng hướng nên bằng nhau
Suy ra \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \). Do đó đáp án B đúng.
+) Hai vec tơ \(\overrightarrow {AM} \) và \(\overrightarrow {MB} \) cùng hướng
Vì M là trung điểm của AB nên AM = MB
Suy ra \(\overrightarrow {AM} = \overrightarrow {MB} \). Do đó đáp án C đúng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
Câu hỏi:
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
A. \(\overrightarrow {DC} \);
B. \(\overrightarrow {AD} \);
C. \(\overrightarrow {CB} \);
D. \(\overrightarrow {BA} \).
Đáp án chính xác
Trả lời:
Đáp án đúng là D
Vì ABCD là hình bình hành nên AB // CD nên \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng phương. Do đó \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng hướng.
Mặt khác AB = CD (tính chất hình bình hành)
Suy ra \(\overrightarrow {BA} = \overrightarrow {CD} \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
A. P(0; 13);
B. Q(1; -8);
Đáp án chính xác
C. H(2; 1);
D. K(3; 1).
Trả lời:
Đáp án đúng là B
Ta có \(\overrightarrow {MN} \left( { – 1; – 4} \right)\). Gọi tọa độ điểm cần tìm là F(x; y).
Khi đó \(\overrightarrow {MF} \left( {x – 3;y + 1} \right)\)
Để M, N, F thẳng hàng khi \(\overrightarrow {MF} \) cùng phương với \(\overrightarrow {MN} \) hay \(\frac{{x – 3}}{{ – 1}} = \frac{{y + 1}}{{ – 4}}\)
⇔ y + 1 = 4(x – 3)
⇔ y= 4x – 12 (1)
+) Xét tọa độ P có x = 0 và y = 13 thay vào (1) ta được 13 = 4.0 – 12 là mệnh đề sai. Do đó loại P.
+) Xét tọa độ Q có x = 1 và y = -9 thay vào (1) ta được -8 = 4.1 – 12 là mệnh đề đúng. Do đó Q thỏa mãn.
+) Xét tọa độ H có x = 2 và y = 1 thay vào (1) ta được 1 = 4.2 – 12 là mệnh đề sai. Do đó loại H.
+) Xét tọa độ K có x = 3 và y = 1 thay vào (1) ta được 1 = 4.3 – 12 là mệnh đề sai. Do đó loại H.
Vậy M, N, Q thẳng hàng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Câu hỏi:
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
A. \(\left| {\overrightarrow {AM} } \right| = \sqrt {53} \)cm
B. \(\left| {\overrightarrow {AM} } \right| = 3\) cm
C. \(\left| {\overrightarrow {AM} } \right| = \frac{{\sqrt {53} }}{2}\) cm
Đáp án chính xác
D. \(\left| {\overrightarrow {AM} } \right| = \frac{3}{2}\) cm
Trả lời:
Đáp án đúng là C
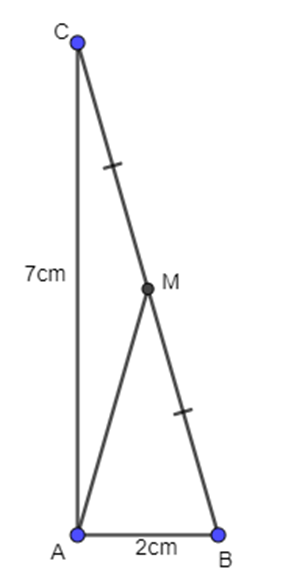
Xét tam giác ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lí Py – ta – go)
⇔ BC2 = 22 + 72 = 4 + 49 = 53
⇔ BC = \(\sqrt {53} \) cm
Ta lại có M là trung điểm BC
⇒ AM = \(\frac{1}{2}\) BC (tính chất đường trung tuyến)
⇒ AM = \(\frac{{\sqrt {53} }}{2}\) cm.
⇒ \(\left| {\overrightarrow {AB} } \right| = AB = \frac{{\sqrt {53} }}{2}cm\)
Vậy độ dài vectơ \(\overrightarrow {AB} \) là \(\frac{{\sqrt {53} }}{2}cm.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
Câu hỏi:
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
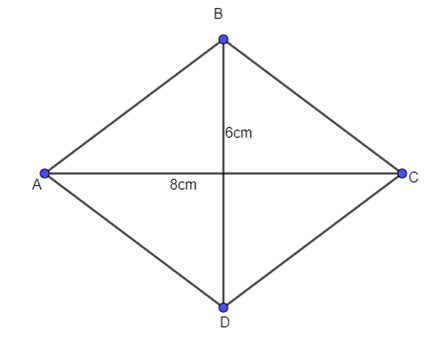
A. 10 cm;
B. 3 cm;
C. 4 cm;
D. 5cm.
Đáp án chính xác
Trả lời:
Đáp án đúng là D
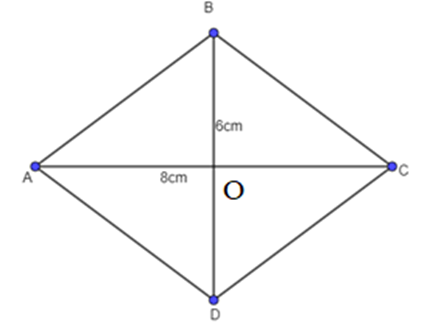
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC, cũng là trung điểm của BD.
⇒ AO = OC = \(\frac{{AC}}{2} = \frac{8}{2} = 4cm.\)
⇒ BO = OD = \(\frac{{BD}}{2} = \frac{6}{2} = 3cm.\)
Xét tam giác AOB vuông tại O, có:
AB2 = AO2 + BO2 (định lí Py – ta – go)
⇔ AB2 = 42 + 32 = 16 + 9 = 25
⇔ AB = 5 (cm)
\( \Rightarrow \left| {\overrightarrow {AB} } \right| = AB = 5cm.\)
Vậy độ dài \(\overrightarrow {AB} \) là 5cm.====== **** mời các bạn xem câu tiếp bên dưới **** =====