Câu hỏi:
Quan sát cây cầu văng minh họa ở Hình 25.
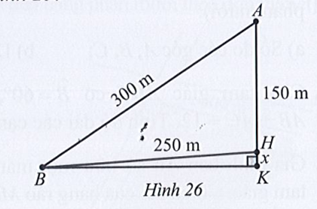
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Trả lời:
Lời giải
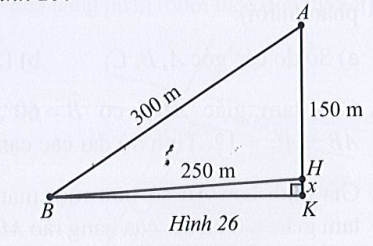
Xét tam giác ABC, có:
\({\rm{cos}}\widehat {AHB} = \frac{{A{H^2} + B{H^2} – A{B^2}}}{{2.AH.BH}} = \frac{{{{150}^2} + {{250}^2} – {{300}^2}}}{{2.150.250}} = – \frac{1}{{15}}\)
⇒ \(\widehat {AHB} \approx 93,8^\circ \)
Ta lại có: \(\widehat {AHB} + \widehat {BHK} = 180^\circ \)
\(\widehat {BHK} = 180^\circ – \widehat {AHB} = 180^\circ – 93,8^\circ = 86,2^\circ \)
Xét tam giác BHK vuông tại K, có:
\(\widehat {HBK} + \widehat {BHK} = 90^\circ \) (hai góc phụ nhau)
⇔ \(\widehat {HBK} = 90^\circ – \widehat {BHK}\)
⇔ \(\widehat {HBK} \approx 90^\circ – 86,2^\circ = 3,8^\circ \).
Vậy độ dốc của cầu qua trụ khoảng 3,8°.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, \(\widehat A = 125^\circ \). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Độ dài cạnh BC;
Câu hỏi:
Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, \(\widehat A = 125^\circ \). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Độ dài cạnh BC;Trả lời:
Lời giải
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
⇔ BC2 = 6,52 + 8,52 – 2.6,5.8,5.cos125°
⇔ BC2 ≈ 177,9
⇔ BC ≈ 13,3.
Vậy BC ≈ 13,3.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số đo các góc B, C;
Câu hỏi:
Số đo các góc B, C;
Trả lời:
Lời giải
Xét tam giác ABC, có:
\(\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2.AB.BC}} = \frac{{{{6,5}^2} + {{13,3}^2} – {{8,5}^2}}}{{2.6,5.13,3}} \approx 0,8\)
⇒ \(\widehat B \approx 31,8^\circ \)
Ta lại có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat C = 180^\circ – \left( {\widehat A + \widehat B} \right) \approx 180^\circ – \left( {125^\circ + 31,8^\circ } \right) = 23,2^\circ \).
Vậy \(\widehat B \approx 31,8^\circ \) và \(\widehat C \approx 23,2^\circ \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Diện tích tam giác ABC.
Câu hỏi:
Diện tích tam giác ABC.
Trả lời:
Lời giải
Diện tích tam giác ABC là:
S = \(\frac{1}{2}.AB.AC.\sin A = \frac{1}{2}.6,5.8,5.\sin 125^\circ \approx 22,6\) (đvdt).
Vậy diện tích tam giác ABC là 22,6 đvdt.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có BC = 50 cm, \(\widehat B = 65^\circ ,\widehat C = 45^\circ \). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Độ dài cạnh AB, AC;
Câu hỏi:
Cho tam giác ABC có BC = 50 cm, \(\widehat B = 65^\circ ,\widehat C = 45^\circ \). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Độ dài cạnh AB, AC;Trả lời:
Lời giải
Xét tam giác ABC, có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc)
⇒ \(\widehat A = 180^\circ – \left( {\widehat B + \widehat C} \right) = 180^\circ – \left( {65^\circ + 45^\circ } \right) = 70^\circ \).
Áp dụng định lí sin trong tam giác ABC, ta được:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
⇔ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }} = 2R\)
⇒ \(\frac{{AB}}{{\sin 45^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AB = \frac{{50.\sin 45^\circ }}{{\sin 70^\circ }} \approx 37,6\)
⇒ \(\frac{{AC}}{{\sin 65^\circ }} = \frac{{50}}{{\sin 70^\circ }}\) ⇔ \(AC = \frac{{50\sin 65^\circ }}{{\sin 70^\circ }} \approx 48,2\)
Vậy AB ≈ 37,6 vậy AC ≈ 48,2.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bán kính đường tròn ngoài tiếp tam giác ABC.
Câu hỏi:
Bán kính đường tròn ngoài tiếp tam giác ABC.
Trả lời:
Lời giải
Áp đụng định lí sin trong tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = 2R \Leftrightarrow \frac{{50}}{{\sin 70^\circ }} = 2R \Leftrightarrow R = \frac{{50}}{{2\sin 70^\circ }} \approx 26,6\).
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 26,6.====== **** mời các bạn xem câu tiếp bên dưới **** =====