Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.

Câu hỏi:

Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.

Trả lời:

Lời giải

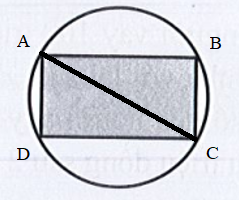
Đặt tọa độ các đỉnh của hình chữ nhật là ABCD.
Vì ABCD nội tiếp hình tròn nên AC là đường kính. Do đó AC = 50 m.
Gọi chiều dài của hình chữ nhật là x (m) (x > 0).
Khi đó AB = DC = x(m)
Xét tam giác ABC vuông tại B, có:
AC² = AB² + BC² (định lý py – ta – go)
⇔ 50² = x² + BC²
⇔ BC² = 2 500 – x²
⇔ BC = \(\sqrt {2500 – {x^2}} \)
Tổng quãng đường đi xung quanh vườn chính là chu vi hình chữ nhật và bằng 140m, nên ta có: 2(x + \(\sqrt {2500 – {x^2}} \)) = 140
⇔ \(\sqrt {2500 – {x^2}} \) = 70 – x (điều kiện x ≤ 70)
⇔ 2 500 – x² = 4 900 – 140x + x²
⇔ 2x² – 140x + 2 400 = 0
⇔ x = 40 (TM) hoặc x = 30 (TM)
Nếu một cạnh bằng 40m thì cạnh còn lại là 30m, nếu một cạnh bằng 30m thì cạnh còn lại là 40m.
Vậy kích thước của hình chữ nhật là 40m và 30m.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các phát biểu sau, phát biểu nào đúng? A. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x). B. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình [f(x)]2 = [g(x)]2. C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \) D. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
   
   

   Câu hỏi:
   

   Trong các phát biểu sau, phát biểu nào đúng?
   A. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x).
   B. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình [f(x)]² = [g(x)]².
   C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)
   D. Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).

   Trả lời:

   Lời giải
   Đáp án đúng là D
   Tập nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)là tập nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong các phát biểu sau, phát biểu nào đúng? A. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\)là tập nghiệm của phương trình f(x) = [g(x)]2. B. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\) là tập nghiệm của phương trình f(x) = [g(x)]2 thỏa mãn bất phương trình g(x) ≥ 0. C. Mọi nghiệm của phương trình f(x) = [g(x)]2 đều là nghiệm của phương trình \(\sqrt {f(x)} = g(x)\). D. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\)là tập nghiệm của phương trình f(x) = [g(x)]2 thỏa mãn bất phương trình f(x) ≥ 0.
   
   

   Câu hỏi:
   

   Trong các phát biểu sau, phát biểu nào đúng?
   A. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\)là tập nghiệm của phương trình f(x) = [g(x)]².
   B. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\) là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0.
   C. Mọi nghiệm của phương trình f(x) = [g(x)]² đều là nghiệm của phương trình \(\sqrt {f(x)} = g(x)\).
   D. Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\)là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình f(x) ≥ 0.

   Trả lời:

   Lời giải
   Đáp án đúng là B.
   Tập nghiệm của phương trình \(\sqrt {f(x)} = g(x)\) là tập nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = g(x) thỏa mãn một trong hai bất phương trình f(x) ≥ 0 hoặc g(x) ≥ 0 mà không cần kiểm tra thỏa mãn đồng thời cả hai bất phương trình đó để kết luận nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \).
   
   

   Câu hỏi:
   

   Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = g(x) thỏa mãn một trong hai bất phương trình f(x) ≥ 0 hoặc g(x) ≥ 0 mà không cần kiểm tra thỏa mãn đồng thời cả hai bất phương trình đó để kết luận nghiệm của phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \).

   Trả lời:

   Lời giải
   Xét phương trình \(\sqrt {f(x)} = \sqrt {g(x)} \)(*)
   Điều kiện tồn tại căn thức là: f(x) ≥ 0 hoặc g(x) ≥ 0
   Bình phương hai vế của phương trình (*) ta được: f(x) = g(x).
   Do đó ta chỉ cần hoặc f(x) ≥ 0 hoặc g(x) ≥ 0 là đủ.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = [g(x)]2 thỏa mãn bất phương trình g(x) ≥ 0 mà không cần kiểm tra thỏa mãn bất phương trình f(x) ≥ 0 để kết luận nghiệm của phương trình \(\sqrt {f(x)} = g(x)\).
   
   

   Câu hỏi:
   

   Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = [g(x)]² thỏa mãn bất phương trình g(x) ≥ 0 mà không cần kiểm tra thỏa mãn bất phương trình f(x) ≥ 0 để kết luận nghiệm của phương trình \(\sqrt {f(x)} = g(x)\).

   Trả lời:

   Lời giải
   Xét \(\sqrt {f(x)} = g(x)\) (**)
   Điều kiện của phương trình gồm:
   +) Điều kiện tồn tại của căn thức là f(x) ≥ 0
   +) Vì \(\sqrt {f(x)} \) ≥ 0 nên g(x) ≥ 0.
   Bình phương 2 vế của phương trình (**) là: f(x) = [g(x)]² ≥ 0
   Do đó trong hai điều kiện ta chỉ cần g(x) ≥ 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giải các phương trình sau: \(\sqrt { – 4x + 4} = \sqrt { – {x^2} + 1} \);
   
   

   Câu hỏi:
   

   Giải các phương trình sau:
   \(\sqrt { – 4x + 4} = \sqrt { – {x^2} + 1} \);

   Trả lời:

   Lời giải
   \(\sqrt { – 4x + 4} = \sqrt { – {x^2} + 1} \) (1)
   Điều kiện – 4x + 4 ≥ 0 ⇔ x ≤ 1
   (1) ⇔ – 4x + 4 = – x² + 1
   ⇔ x² – 4x + 3 = 0
   ⇔ x = 3 (không thỏa mãn) và x = 1 (thỏa mãn)
   Vậy nghiệm của phương trình là x = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====