Câu hỏi:
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và Y để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại X là 250 nghìn đồng, giá một bao loại Y là 200 nghìn đồng. Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc X và Y sao cho hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.
Trả lời:
Đáp án đúng là: A
Gọi số bao loại X và số bao loại Y lần lượt là x bao và y bao (x, y ℕ).
Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C nên x bao loại X chứa 2x đơn vị chất dinh dưỡng A, 2x đơn vị chất dinh dưỡng B và 2x đơn vị chất dinh dưỡng C.
Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C nên y bao loại Y chứa y đơn vị chất dinh dưỡng A, 9y đơn vị chất dinh dưỡng B và 3y đơn vị chất dinh dưỡng C.
Hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C nên 2x + y ≥ 12; 2x + 9y ≥ 36; 2x + 3y ≥ 24.
Khi đó ta có hệ bất phương trình sau 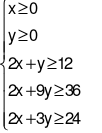
F(x; y) = 250x + 200y (triệu đồng).
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(5; 5) d1 và thay vào biểu thức x ta được 5 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(5; 5).
• Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(5; 5) d2 và thay vào biểu thức y ta được 5 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 chứa điểm I(5; 5).
• Vẽ đường thẳng d3: 2x + y = 12 bằng cách vẽ đường thẳng đi qua hai điểm (6; 0) và (5; 2).
Chọn điểm I(5; 5) d3 và thay vào biểu thức 2x + y ta được 2 . 5 + 5 = 15 > 12.
Suy ra miền nghiệm của bất phương trình 2x + y ≥ 12 là nửa mặt phẳng bờ d3 chứa điểm I(5; 5).
• Vẽ đường thẳng d4: 2x + 9y = 36 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4,5; 3).
Chọn điểm I(5; 5) d4 và thay vào biểu thức 2x + 9y ta được 2 . 5 + 9 . 5 = 55 > 36.
Suy ra miền nghiệm của bất phương trình 2x + 9y ≥ 36 là nửa mặt phẳng bờ d4 chứa điểm I(5; 5).
• Vẽ đường thẳng d5: 2x + 3y = 24 bằng cách vẽ đường thẳng đi qua hai điểm (3; 6) và (6; 4).
Chọn điểm I(5; 5) d5 và thay vào biểu thức 2x + 3y ta được 2 . 5 + 3 . 5 = 25 > 24.
Suy ra miền nghiệm của bất phương trình 2x + 3y ≥ 24 là nửa mặt phẳng bờ d5 chứa điểm I(5; 5).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
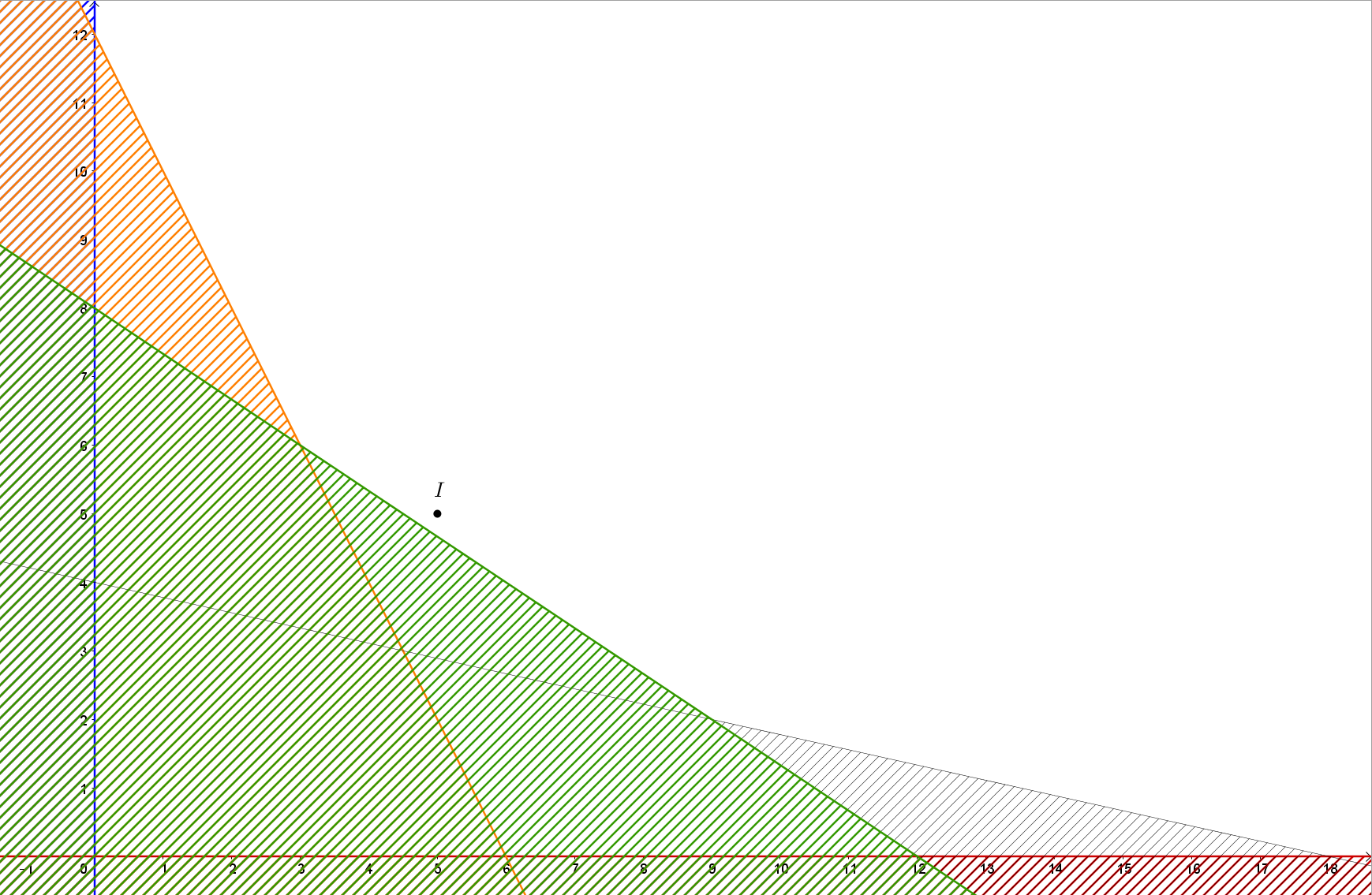
Miền nghiệm của hệ được giới hạn bởi các điểm (0; 12); (3; 6); (9; 2); (18; 0).
Ta có:
F(0; 12) = 250 . 0 + 200 . 12 = 2 400;
F(3; 6) = 250 . 3 + 200 . 6 = 1 950;
F(9; 2) = 250 . 9 + 200 . 2 = 2 650;
F(18; 0) = 250 . 18 + 200 . 0 = 4 500.
Khi đó ta thấy F(x; y) đạt giá trị nhỏ nhất bằng 1 950 tại x = 3; y = 6.
Vậy chi phí nhỏ nhất để mua hai loại thức ăn là 1,95 triệu đồng.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Câu hỏi:
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 2x2 + 3y > 4.
B. xy + x < 5.
C. 32x + 43y ≥ 6.
Đáp án chính xác
D. x + y3 ≤ 3.
Trả lời:
Đáp án đúng là: C
Phương án A có x2 là hạng tử bậc 2.
Phương án B có xy là hạng tử bậc 2.
Phương án D có y3 là hạng tử bậc 3.
Phương án C có các hạng tử đều có bậc bằng 1.
Vậy ta chọn phương án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
Câu hỏi:
Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
A.
 .
.B.
 .
.Đáp án chính xác
C.
 .
.D.
 .
.Trả lời:
Đáp án đúng là: B
Phương án A có y2 là hạng tử bậc 2.
Phương án C có y2 là hạng tử bậc 2.
Phương án D có xy là hạng tử bậc 2.
Phương án B có các hạng tử đều có bậc bằng 1.
Vậy ta chọn phương án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y ≤ 10?
Câu hỏi:
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y ≤ 10?
A. (5; 2).
B. (-1; 4).
C. (2; 1).
Đáp án chính xác
D. (-5; 6).
Trả lời:
Đáp án đúng là: C
Thay x = 4; y = 2 vào biểu thức 2x + 5y ta được 2 . 4 + 5. 2 = 18 > 10 nên phương án A không thỏa mãn.
Thay x = -1; y = 4 vào biểu thức 2x + 5y ta được 2 . (-1) + 5 . 4 = 18 > 10 nên phương án B không thỏa mãn.
Thay x = -5; y = 6 vào biểu thức 2x + 5y ta được 2 . (-5) + 5 . 6 = 20 > 10 nên phương án D không thỏa mãn.
Thay x = 2; y = 1 vào biểu thức 2x + 5y ta được 2 . 2 + 5 . 1 = 9 < 10 nên phương án C đúng.
Vậy ta chọn phương án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x – 3y > 13?
Câu hỏi:
Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x 3y > 13?
A. (1; -5).
B. (2; -4).
C. (3; -3).
D. (8; 1).
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Thay x = 1; y = -5 vào biểu thức 2x 3y ta được 2 . 1 3 . (-5) = 17 > 13 nên phương án A không thỏa mãn.
Thay x = 2; y = -4 vào biểu thức 2x 3y ta được 2 . 2 3 . (-4) = 16 > 13 nên phương án B không thỏa mãn.
Thay x = 3; y = -3 vào biểu thức 2x 3y ta được 2 . 3 3 . (-3) = 15 > 13 nên phương án C không thỏa mãn.
Thay x = 8; y = 1 vào thức 2x 3y ta được 2 . 8 3 . 1 = 13 nên phương án D đúng.
Vậy ta chọn phương án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho bất phương trình x + 2y ≤ 3. Khẳng định nào sau đây là đúng?
Câu hỏi:
Cho bất phương trình x + 2y ≤ 3. Khẳng định nào sau đây là đúng?
A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc tọa độ.
Đáp án chính xác
B. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 không chứa gốc tọa độ.
C. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = -3 chứa gốc tọa độ.
D. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = -3 không chứa gốc tọa độ.
Trả lời:
Đáp án đúng là: A
Bất phương trình x + 2y ≤ 3 nên miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3.
Do đó đáp án C và D không thỏa mãn.
Thay x = 0; y = 0 vào biểu thức x + 2y ta được 0 + 2 . 0 = 0 < 3.
Suy ra miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc tọa độ.
Vậy ta chọn phương án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====