Một hộp kín có 1 quả bóng xanh và 5 quả bóng đỏ có kích thước và khối lượng bằng nhau. Hỏi Dũng cần lấy ra từ hộp ít nhất bao nhiêu quả bóng để xác suất lấy được quả bóng xanh lớn hơn 0,5?

Câu hỏi:

Một hộp kín có 1 quả bóng xanh và 5 quả bóng đỏ có kích thước và khối lượng bằng nhau. Hỏi Dũng cần lấy ra từ hộp ít nhất bao nhiêu quả bóng để xác suất lấy được quả bóng xanh lớn hơn 0,5?

Trả lời:

Gọi k là số quả bóng Dũng lấy ra (k $\in$ ℕ, 1 ≤ k ≤ 6).
Số phần tử của không gian mẫu: n(Ω) = $C_6^k$ 
Vì xác suất lấy được quả bóng xanh lớn hơn 0,5 mà chỉ có 1 quả bóng xanh nên số bóng đỏ được chọn là k – 1
Ta có $\frac{C_5^{k-1}}{C_6^k}>0,5$
 $\iff \frac{5!}{(k-1)!.(5-(k-1\left)\right)!}>0,5.\frac{6!}{k!(6-k)!}$
$\iff \frac{120}{(k-1)!.(6-k)!}>0,5.\frac{720}{k.(k-1)!.(6-k)!}$ 
$\iff$120k > 360
$\iff$k > 3
Vậy để xác suất lấy được quả bóng xanh lớn hơn 0,5 thì Dũng phải chọn ít nhất 4 quả bóng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Gieo một con xúc xắc 4 mặt cân đối và đồng chất ba lần. Tính xác suất của các biến cố: a) “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2”;
   
   

   Câu hỏi:
   

   Gieo một con xúc xắc 4 mặt cân đối và đồng chất ba lần. Tính xác suất của các biến cố:
   a) “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2”;

   Trả lời:

   a) Biến cố “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2” đây là biến cố chắc chắn nên ta có P(A) = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. b) “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”.
   
   

   Câu hỏi:
   

   b) “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”.

   Trả lời:

   b) Số phần tử của không gian mẫu n(Ω) = 4³ = 64
   Gọi B là biến cố: “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”
   Trường hợp 1. Lần thứ nhất số xuất hiện ở đỉnh phía trên của con xúc xắc là 2
   Vì có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2 nên số xuất hiện ở hai lần sau phải khác 2 nên mỗi lần có 3 kết quả sảy ra
   Ta có 1.3² = 9 kết quả thuận lợi
   Trường hợp 2. Lần thứ hai số xuất hiện ở đỉnh phía trên của con xúc xắc là 2
   Tương tự trường hợp 1 có 1.3² = 9 kết quả thuận lợi
   Trường hợp 3. Lần thứ ba số xuất hiện ở đỉnh phía trên của con xúc xắc là 2
   Tương tự trường hợp 1 có 1.3² = 9 kết quả thuận lợi
   Số phần tử của biến cố B là: n(B) = 9 + 9 + 9 = 27
   Xác suất của biến cố B là: P(B) = $\frac{27}{64}$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tung một đồng xu cân đối và đồng chất bốn lần. Tính xác suất của các biến cố: a) “Cả bốn lần đều xuất hiện mặt giống nhau”;
   
   

   Câu hỏi:
   

   Tung một đồng xu cân đối và đồng chất bốn lần. Tính xác suất của các biến cố:
   a) “Cả bốn lần đều xuất hiện mặt giống nhau”;

   Trả lời:

   Số phần tử của không gian mẫu n(Ω) = 2⁴ = 16
   a) Gọi A là biến cố: “Cả bốn lần đều xuất hiện mặt giống nhau”
   A = {SSSS; NNNN}
   Số phần tử của biến cố A là: n(A) = 2
   Xác suất của biến cố A là: P(A) = $\frac{2}{16}=\frac{1}{8}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. b) “Có đúng một lần xuất hiện mặt sấp, ba lần xuất hiện mặt ngửa”.
   
   

   Câu hỏi:
   

   b) “Có đúng một lần xuất hiện mặt sấp, ba lần xuất hiện mặt ngửa”.

   Trả lời:

   b) Gọi B là biến cố: “Có đúng một lần xuất hiện mặt sấp, ba lần xuất hiện mặt ngửa”
   B = {SNNN; NSNN; NNSN; NNNS}
   Số phần tử của biến cố B là: n(B) = 4.
   Xác suất của biến cố B là: P(B) = $\frac{4}{16}=\frac{1}{4}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
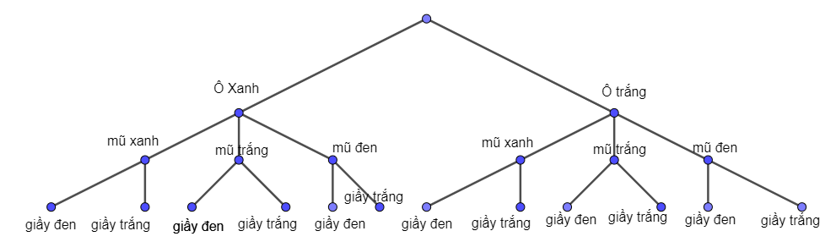
5. Chi có 1 cái ô xanh, 1 cái ô trắng; 1 cái mũ xanh, l cải mũ trắng, 1 cái mũ đen; 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, l cái mũ và l đôi giày để đến trường. a) Hãy vẽ sơ đồ cây mô tả các kết quả có thể xảy ra.
   
   

   Câu hỏi:
   

   Chi có 1 cái ô xanh, 1 cái ô trắng; 1 cái mũ xanh, l cải mũ trắng, 1 cái mũ đen; 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, l cái mũ và l đôi giày để đến trường.
   a) Hãy vẽ sơ đồ cây mô tả các kết quả có thể xảy ra.

   Trả lời:

   a) Sơ đồ cây mô tả các kết quả có thể xảy ra
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====