Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki ‒ lo ‒ gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi ki ‒ lo ‒ gam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Giá trị x2 + y2 là:

Câu hỏi:

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki ‒ lo ‒ gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi ki ‒ lo ‒ gam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 250 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Giá trị x² + y² là:

A. 1

B. 1,2;

C. 1,3

Đáp án chính xác

D. 1,5

Trả lời:

Hướng dẫn giải
Đáp án đúng là: C
Gia đình chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn nên 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1.
Mỗi ki ‒ lo ‒ gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit; mỗi ki ‒ lo ‒ gam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit mà gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên:
 $\left\{\begin{array}{l}800x+600y\ge 900\\ 200x+400y\ge 400\end{array}\right.\iff \left\{\begin{array}{l}8x+6y\ge 9\\ x+2y\ge 2\end{array}\right.$
Ta có hệ bất phương trình:  $\left\{\begin{array}{l}0\le x\le 1,6\\ 0\le y\le 1,1\\ 8x+6y\ge 9\\ x+2y\ge 2\end{array}\right.\iff \left\{\begin{array}{l}x\ge 0\\ x\le 1,6\\ y\ge 0\\ y\le 1,1\\ 8x+6y\ge 9\\ x+2y\ge 2\end{array}\right.$
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục toạ độ Oxy:
– Biểu diễn miền nghiệm D₁ của bất phương trình x ≥ 0.
+ Đường thẳng x = 0 là trục Oy.
Miền nghiệm D₁ của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy (kể cả bờ Oy) nằm bên phải trục Oy.
* Tương tự ta biểu diễn các miền nghiệm:
– Miền nghiệm D₂ của bất phương trình y ≥ 0: là nửa mặt phẳng bờ Ox (kể cả bờ Ox) nẳm bên trên trục Ox.

– Miền nghiệm D₃ của bất phương trình x ≤ 1,6: là nửa mặt phẳng bờ d₁ (kể cả bờ d₁: x = 1,6) chứa điểm O.
– Miền nghiệm D₄ của bất phương trình y ≤ 1,1: là nửa mặt phẳng bờ d₂ (kể cả bờ d₂: y = 1,1) chứa điểm O.
– Miền nghiệm D₅ của bất phương trình 8x + 6y ≥ 9.
+ Vẽ đường thẳng d₃: 8x + 6y = 9.
+ Xét điểm O(0; 0): Thay x = 0, y = 0 vào bất phương trình ta có 8. 0 + 6. 0 = 0 ≥ 9 là mệnh đề sai nên điểm O(0; 0) không thỏa mãn bất phương trình 8x + 6y ≥ 9.
Miền nghiệm D₅ của bất phương trình 8x + 6y ≥ 9 là nửa mặt phẳng bờ d₃ (kể cả bờ d₃) không chứa điểm O.
– Tương tự miền nghiệm D₆ của bất phương trình x + 2y ≥ 2 là nửa mặt phẳng bờ d₄ (kể cả bờ d₄) không chứa điểm O.
Ta có đồ thị:

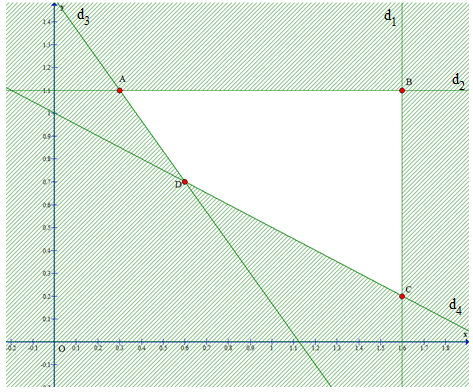
Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD:
A(0,3; 1,1), B(1,6; 1,1), C(1,6; 0,2), D(0,6; 0,7).
Giá tiền một kg thịt bò là 250 nghìn đồng, một kg thịt lợn là 110 nghìn đồng nên tổng số tiền cần mua là F (x; y) = 250x + 110y (nghìn đồng) phải nhỏ nhất.
Tại A(0,3; 1,1), F = 250. 0,3 + 110. 1,1 = 196;
Tại B(1,6; 1,1), F = 250. 1,6 + 110. 1,1 = 521;
Tại C(1,6; 0,2), F = 250. 1,6 + 110. 0,2 = 422;
Tại D(0,6; 0,7), F = 250. 0,6 + 110. 0,7 = 227.
Vậy F (x; y) nhỏ nhất là 196 khi x = 0,3 và y = 1,1.
Khi đó x² + y² = 0,3² + 1,1² = 1,3.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Điểm O(0; 0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
   
   

   Câu hỏi:
   

   Điểm O(0; 0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

   A. $\left\{\begin{array}{l}x+3y-6>0\\ 2x+y+4>0\end{array}\right.$

   B. $\left\{\begin{array}{l}x+3y-6>0\\ 2x+y+4<0\end{array}\right.$

   C. $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4>0\end{array}\right.$

   Đáp án chính xác

   D. $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4<0\end{array}\right.$

   Trả lời:

   Đáp án đúng là: C
   Thay điểm O(0; 0) vào từng đáp án ta có :
   Đáp án A, B sai vì 0 + 3.0 – 6 < 0 không thỏa mãn bất phương trình x + 3y – 6 > 0.
   Đáp án D sai vì 2.0 + 0 + 4 > 0 không thỏa mãn bất phương trình 2x + y + 4 < 0.
   Đáp án C 0 + 3.0 – 6 < 0 thỏa mãn, 2.0 + 0 + 4 > 0 thỏa mãn
   Vậy đáp án đúng là C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương trình x+3y−2≥02x+y+1≤0
   
   

   Câu hỏi:
   

   Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+3y-2\ge 0\\ 2x+y+1\le 0\end{array}\right.$

   A. (0; 1);

   B. (– 1; 1);

   Đáp án chính xác

   C. (1; 3);

   D. (– 1; 0).

   Trả lời:

   Đáp án đúng là: B
   Xét đáp A: Thay toạ độ từ đáp án vào hệ bất phương trình ta có $\left\{\begin{array}{l}0+3.1-2>0\\ 2.0+1+1>0\end{array}\right.$  không thỏa mãn hệ bất phương trình.
   Xét đáp án B: Thay toạ độ từ đáp án vào hệ bất phương trình ta có $\left\{\begin{array}{l}-1+3.1-2=0\\ 2.(-1)+1+1=0\end{array}\right.$  thỏa mãn hệ bất phương trình
   Xét đáp án C: Thay toạ độ từ đáp án vào hệ bất phương trình ta có $\left\{\begin{array}{l}1+3.3-2>0\\ 2.1+3+1>0\end{array}\right.$  không thỏa mãn hệ bất phương trình
   Xét đáp án D: Thay toạ độ từ đáp án vào hệ bất phương trình ta có $\left\{\begin{array}{l}-1+3.0-2<0\\ 2.(-1)+3+1>0\end{array}\right.$  không thỏa mãn hệ bất phương trình
   Vậy đáp án đúng là B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ: y−2x≤22y−x≥4x+y≤5là:
   
   

   Câu hỏi:
   

   Giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ: $\left\{\begin{array}{c}y-2x\le 2\\ 2y-x\ge 4\\ x+y\le 5\end{array}\right.$là:

   A. min F(x; y) = 1 khi x = 2, y = 3;

   Đáp án chính xác

   B. min F(x; y) = 2 khi x = 0, y = 2;

   C. min F(x; y) = 3 khi x = 1, y = 4;

   D. min F(x; y) = 7 khi x = 6, y = – 1.

   Trả lời:

   Đáp án Đúng là: A
   Ta tìm miền nghiệm xác định bởi hệ
   Vẽ đường thẳng d₁: y – 2x = 2, đường thẳng d₁ qua hai điểm (0; 2) và (– 1; 0).
   Ta xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 – 2.0 = 0 < 2.
   Do đó điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm D₁ là nửa mặt phẳng được chia bởi đường thẳng d₁ chứa gốc tọa độ O kể cả bờ.
   Vẽ đường thẳng d₂: 2y – x = 4, đường thẳng d₂ qua hai điểm (0; 2) và (– 4; 0).
   Ta xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 – 0 = 0 < 4 không thoả mãn bất phương trình 2y – x ≥ 4.
   Do đó điểm O(0; 0) không thuộc nềm nghiệm của bất phương trình. Vậy miền nghiệm D₂ là nửa mặt phẳng được chia bởi đường thẳng d₂ không chứa gốc tọa độ O kể cả bờ.
   Vẽ đường thẳng d₃: x + y = 5, đường thẳng d₁ qua hai điểm (0; 5) và (5; 0).
   Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 0 = 0 < 5, thoả mãn bất phương trình x + y ≤ 5.
   Do đó điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm D₃ là nửa mặt phẳng được chia bởi đường thẳng d₃ chứa gốc tọa độ O kể cả bờ.
   Miền nghiệm là phần không gạch chéo như hình vẽ.
   
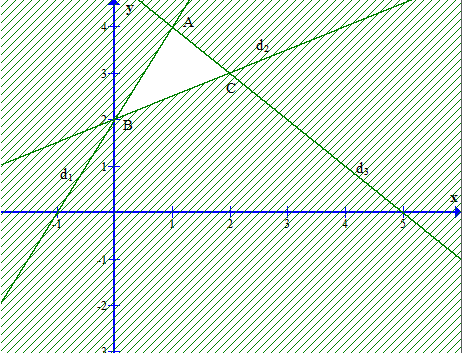
   Miền nghiệm của hệ là tam giác ABC với A(1; 4), B(0; 2), C(2; 3).
   Ta tính giá trị của F(x; y) = y – x tại các giao điểm:
   Tính F(x; y) = y – x suy ra F(1; 4) = 4 – 1 = 3.
   Tính F(x; y) = y – x suy ra F(0; 2) = 2 – 0 = 2.
   Tính F(x; y) = y – x suy ra F(2; 3) = 3 – 2 = 1.
   Vậy min F(x; y) = 1 khi x = 2, y = 3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình x+y−2≤02x−3y+2>0  là
   
   

   Câu hỏi:
   

   Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình $\left\{\begin{array}{c}x+y-2\le 0\\ 2x-3y+2>0\end{array}\right.$  là

   A. (0; 0);

   B. (1; 1);

   C. (– 1; 1);

   Đáp án chính xác

   D. (– 1; – 1).

   Trả lời:

   Đáp án đúng là: C
   Xét đáp án A ta có: $\left\{\begin{array}{c}0+0-2<0\\ 2.0-3.0+2>0\end{array}\right.$  đáp án A thoả mãn hệ bất phương trình
   Xét đáp án B ta có : $\left\{\begin{array}{c}1+1-2=0\\ 2.1-3.1+2>0\end{array}\right.$  đáp án B thoả mãn hệ bất phương trình
   Xét đáp án C ta có : $\left\{\begin{array}{c}-1+1-2<0\\ 2.(-1)-3.1+2<0\end{array}\right.$  đáp án C không  thoả mãn hệ bất phương trình
   Xét đáp án D ta có : $\left\{\begin{array}{c}-1+(-1)-2<0\\ 2.(-1)-3.(-1)+2>0\end{array}\right.$  đáp án D thoả mãn hệ bất phương trình
   Vậy đáp án đúng là C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hệ 2x+3y
   
   

   Câu hỏi:
   

   Cho hệ $\left\{\begin{array}{l}2x+3y<5\left(1\right)\\ x+\frac{3}{2}y<5\left(2\right)\end{array}\right.$ . Gọi S₁ là tập nghiệm của bất phương trình (1), S₂ là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì

   A. $S_1\subset S_2$ ;

   Đáp án chính xác

   B. $S_2\subset S_1$;

   C. S₂ = S;

   D. S₁ ≠ S.

   Trả lời:

   Đáp án đúng là: A
   Trước hết, ta vẽ hai đường thẳng:
   (d₁): 2x + 3y = 5
   Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 + 3.0 = 0 < 5, thoả mãn bất phương trình 2x + 3y < 5. Vậy O(0; 0) thuộc miền nghiệm của bất phương trình. Miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch chéo(không kể biên) của (d₁)
   Vẽ đường thẳng (d₂):$x+\frac{3}{2}y=5$ .
   Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có $0+\frac{3}{2}.0=0<5$ , thoả mãn bất phương trình $x+\frac{3}{2}y<5$ . Vậy O(0; 0) thuộc miền nghiệm của bất phương trình. Miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch chéo(không kể biên) của (d₂).
   Miền nghiệm được biểu diễn trong hình dưới đây
   
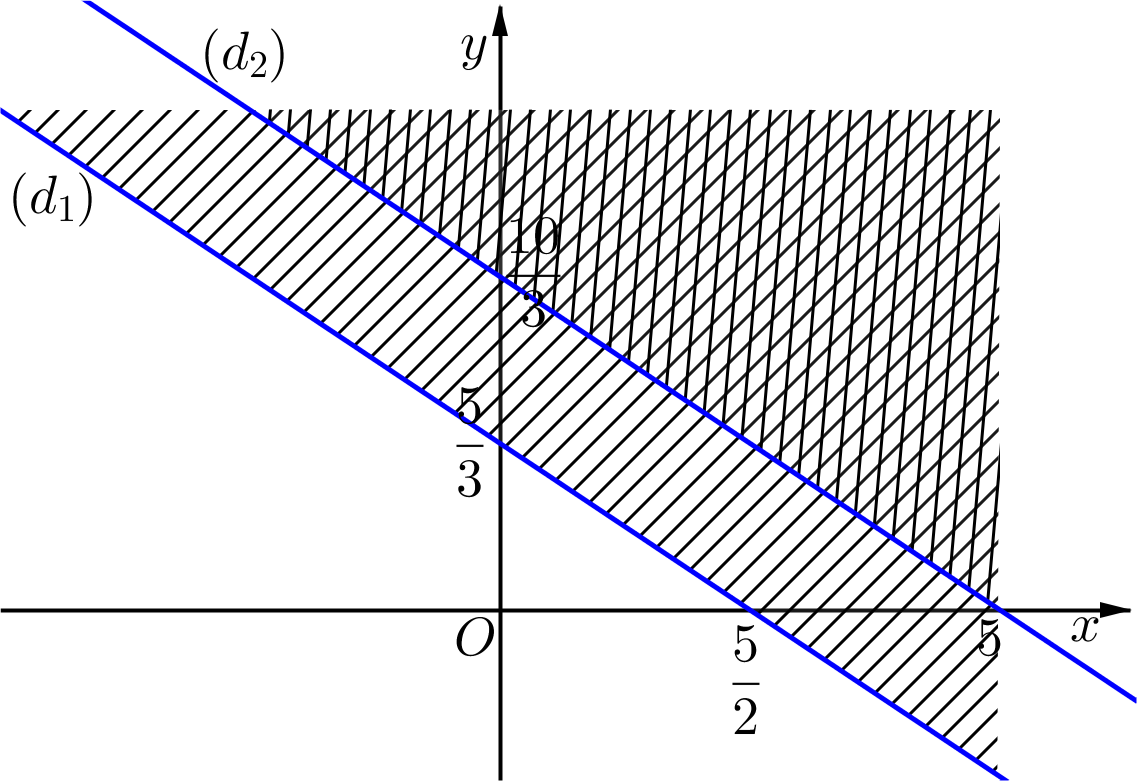
   Từ đồ thị biểu diễn miền nghiệm của hệ bất phương trình ta có $S_1\subset S_2$ ; S₁ = S; S₂ $\ne$ S. Vậy $S_1\subset S_2$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====