Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.

Câu hỏi:

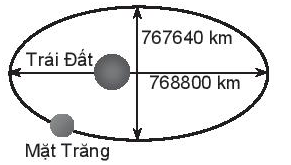
Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.

Trả lời:

Hướng dẫn giải
Xét đường elip như hình vẽ:

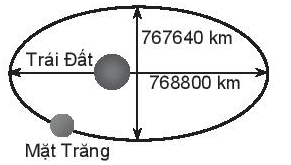
Theo đề bài: Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Nên ta có:
2a = 768 800 và 2b = 767 640
Do đó, a = 384 400 và b = 383 820.
Từ đó suy ra \(c = \sqrt {{a^2} – {b^2}} = \sqrt {{{384400}^2} – {{383820}^2}} \approx 21108\).
Vì vậy,
Khoảng cách lớn nhất từ tâm của Trái Đất đến Mặt Trăng là
a + c ≈ 384 400 + 21 108 = 405 508 (km)
Khoảng cách nhỏ nhất từ tâm của Trái Đất đến Mặt Trăng là:
a – c ≈ 384 400 – 21 108 = 363 292 (km).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho elip (E) có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\). Tìm tiêu điểm và tiêu cự của elip.
   
   

   Câu hỏi:
   

   Cho elip (E) có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\). Tìm tiêu điểm và tiêu cự của elip.

   Trả lời:

   Hướng dẫn giải
   Dựa vào phương trình chính tắc \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\) của (E) ta có
   \(\left\{ {\begin{array}{*{20}{c}}{{a^2} = 36}\\{{b^2} = 16}\end{array}} \right. \Rightarrow c = \sqrt {{a^2} – {b^2}} = 2\sqrt 5 \)
   Vậy (E) có hai tiêu điểm là: \({F_1}\left( { – 2\sqrt 5 ;0} \right),{F_2}\left( {2\sqrt 5 ;0} \right)\)và có tiêu cự là: \(2c = 4\sqrt 5 \).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hypebol (H) có phương trình\(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol.
   
   

   Câu hỏi:
   

   Cho hypebol (H) có phương trình\(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{{20}} = 1\). Tìm tiêu điểm và tiêu cự của hypebol.

   Trả lời:

   Hướng dẫn giải
   Dựa vào phương trình chính tắc \(\frac{{{x^2}}}{{16}} – \frac{{{y^2}}}{{20}} = 1\) của (H) ta có
   \(\left\{ {\begin{array}{*{20}{c}}{{a^2} = 16}\\{{b^2} = 20}\end{array}} \right. \Rightarrow c = \sqrt {{a^2} + {b^2}} = 6\)
   Vậy (H) có hai tiêu điểm là F₁ (–6; 0), F₂(6; 0) và có tiêu cự là 2c = 12.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho parabol (P) có phương trình y2 = 4x. Tìm tiêu điểm và đường chuẩn của parabol.
   
   

   Câu hỏi:
   

   Cho parabol (P) có phương trình y² = 4x. Tìm tiêu điểm và đường chuẩn của parabol.

   Trả lời:

   Hướng dẫn giải
   Dựa vào phương trình chính tắc y² = 4x của (P) ta có:
   2p = 4 ⇔ p = 2 ⇔ \(\frac{p}{2} = 1\) .
   Vậy (P) có tiêu điểm là F(1; 0) và có đường chuẩn là Δ: x = –1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.

   Trả lời:

   Hướng dẫn giải
   Phương trình chính tắc của (E) có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó a > b > 0)
   Vì (E) đi qua điểm A(6; 0) nên ta có \(\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1\) ⇔ a² = 6²
   Do (E) có tiêu cự là 2c = 8 nên ta có c = 4 ⇒ b² = a² – c² = 6² – 4² = 20.
   Vậy phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm \(M\left( {3\sqrt 2 ; – 4} \right)\)và có một tiêu điểm là F2(5; 0).
   
   

   Câu hỏi:
   

   Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm \(M\left( {3\sqrt 2 ; – 4} \right)\)và có một tiêu điểm là F₂(5; 0).

   Trả lời:

   Hướng dẫn giải
   Phương trình chính tắc của (H) có dạng: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó a, b > 0)
   Do (H) có một tiêu điểm là F₂(5; 0) nên ta có:
   c = 5 ⇒ b² + a² = c² = 25 ⇔ a² = 25 – b²
   Vì (H) đi qua điểm \(M\left( {3\sqrt 2 ;4} \right)\)nên ta có
   \(\frac{{{{\left( {3\sqrt 2 } \right)}^2}}}{{{a^2}}} – \frac{{{4^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{{18}}{{{a^2}}} – \frac{{16}}{{{b^2}}} = 1\)                  (1)
   Đặt t = b² (t > 0) ⇒ a² = 25 – t. Thay vào (1) ta được
   \(\frac{{18}}{{25 – t}} – \frac{{16}}{t} = 1\)
   ⇒ 18t – 16(25 – t) = (25 – t)t
   ⇔ 18t – 400 + 16t = 25t – t²
   ⇔ t² + 9t – 400 = 0
   ⇔ t = 16 (thỏa mãn) hoặc t = –25 (không thỏa mãn)
   Do đó, b² = t = 16, a² = 25 – t = 9.
   Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{9} – \frac{{{y^2}}}{{16}} = 1\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====