Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8. Độ dài cạnh kề với cạnh có độ dài bằng 4 là:

Câu hỏi:

Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8. Độ dài cạnh kề với cạnh có độ dài bằng 4 là:

A. 5;

B. $\sqrt{34}$ 

Đáp án chính xác

C. 6;

D. $\sqrt{42}$ 

Trả lời:

Hướng dẫn giải
Đáp án đúng là B:

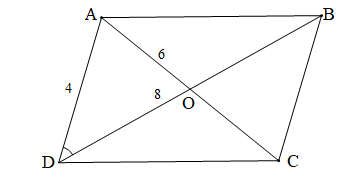
Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8 được mô tả như hình vẽ, do đó AD = 4, AC = 6, BD = 8.
Gọi O là giao điểm của hai đường chéo.
Khi đó O là trung điểm của AC và BD (tính chất hình bình hành).
Þ AO = 3 và DO = 4.
Áp dụng hệ quả định lí côsin vào tam giác ADO ta có:
$cos\widehat{ADO}=\frac{A{D}^2+D{O}^2-A{O}^2}{2.AD.DO}=\frac{4^2+4^2-3^2}{\mathrm{2.4.4}}=\frac{23}{32}$ $\Rightarrow cos\widehat{ADB}=\frac{23}{32}$
Áp dụng định lí côsin vào tam giác ABD ta có:
AB² = AD² + BD² – 2.AD.BD.$cos\widehat{ADB}$ 
Þ AB² = 4² + 8² – 2.4.8.$\frac{23}{32}$ = 34
$\Rightarrow AB=\sqrt{34}.$ 
Vậy độ dài cạnh kề với cạnh có độ dài bằng 4 của hình bình hành đó là $\sqrt{34}$ 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tam giác ABC có BC=55,AC=52,AB=5. Số đo góc A^ là:
   
   

   Câu hỏi:
   

   Tam giác ABC có $BC=5\sqrt{5},AC=5\sqrt{2},AB=5$. Số đo góc $\widehat{A}$ là:

   A. 30°;

   B. 45°;

   C. 120°;

   D. 135°.

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
   $\cos A=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{5^2+{\left(5\sqrt{2}\right)}^2-{\left(5\sqrt{5}\right)}^2}{\mathrm{2.5.5}\sqrt{2}}=-\frac{\sqrt{2}}{2}$
   $\Rightarrow \widehat{A}=135°.$ 
   Vậy $\widehat{A}=135°.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tam giác ABC có A^=105°,B^=45°, AC = 10. Độ dài cạnh AB là:
   
   

   Câu hỏi:
   

   Tam giác ABC có $\widehat{A}=105°,\widehat{B}=45°$, AC = 10. Độ dài cạnh AB là:

   A. $\frac{5\sqrt{6}}{2};$

   B. $5\sqrt{2};$

   Đáp án chính xác

   C. $5\sqrt{6};$

   D. $10\sqrt{2}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Xét tam giác ABC có $\widehat{A}=105°,\widehat{B}=45°$ ta có:
   $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác)
   $\Rightarrow \widehat{C}=180°-\widehat{A}-\widehat{B}$ 
   $\Rightarrow \widehat{C}=180°-105°-45°=30°$
   Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AC}{\sin B}=\frac{AB}{\sin C}$
   $\Rightarrow \frac{10}{\sin 45°}=\frac{AB}{\sin 30°}\Rightarrow AB=\frac{10.\sin 30°}{\sin 45°}=5\sqrt{2}.$
   Vậy $AB=5\sqrt{2}.$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tam giác ABC có AC=33, AB = 3, BC = 6. Số đo góc B là:
   
   

   Câu hỏi:
   

   Tam giác ABC có $AC=3\sqrt{3},$ AB = 3, BC = 6. Số đo góc B là:

   A. 30°;

   B. 45°;

   C. 60°;

   Đáp án chính xác

   D. 120°.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
   $\cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{3^2+6^2-{\left(3\sqrt{3}\right)}^2}{\mathrm{2.3.6}}=\frac{1}{2}$
   $\Rightarrow \widehat{B}=60°.$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, AC=R2. Tính số đo của A^ biết A^ là góc tù.
   
   

   Câu hỏi:
   

   Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, $AC=R\sqrt{2}.$ Tính số đo của $\widehat{A}$ biết $\widehat{A}$ là góc tù.

   A. 105°;

   Đáp án chính xác

   B. 120°;

   C. 135°;

   D. 150°.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Trong tam giác ABC có $\widehat{A}$ là góc tù nên $\widehat{B},\widehat{C}$ là góc nhọn.
   Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AC}{\sin B}=\frac{AB}{\sin C}=2R$ 
   $\Rightarrow \frac{R\sqrt{2}}{\sin B}=\frac{R}{\sin C}=2R$ 
   $\Rightarrow \left\{\begin{array}{l}\sin B=\frac{R\sqrt{2}}{2R}=\frac{\sqrt{2}}{2}\\ sinC=\frac{R}{2R}=\frac{1}{2}\end{array}\right.$ $\Rightarrow \left\{\begin{array}{l}\widehat{B}=45°\\ \widehat{C}=30°\end{array}\right.$ (vì $\widehat{B},\widehat{C}$ là góc nhọn)
   Xét tam giác ABC có $\widehat{B}=45°,\widehat{C}=30°$ ta có:
   $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác)
   $\Rightarrow \widehat{A}=180°-\widehat{B}-\widehat{C}$ 
   $\Rightarrow \widehat{A}=180°-45°-35°=105°$
   Vậy $\widehat{A}=105°$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?

   A. $\frac{\sqrt{15}}{8};$

   B. $\frac{7}{8};$

   Đáp án chính xác

   C. $\frac{1}{2}$

   D. $\frac{\sqrt{14}}{8}.$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.
   Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.
   Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
   $\cos C=\frac{A{C}^2+B{C}^2-A{B}^2}{2.AC.BC}=\frac{3^2+4^2-2^2}{\mathrm{2.3.4}}=\frac{7}{8}.$
   Vậy côsin của góc nhỏ nhất trong tam giác bằng $\frac{7}{8}$ 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====