Giá trị của biểu thức  A=cot 44o+tan 226o.cos 406ocos 316o-cot 72o. cot 18o bằng

Câu hỏi:

Giá trị của biểu thức 
$A=\frac{\left(cot {44}^o+\tan {226}^o\right).\cos {406}^o}{\cos {316}^o}–cot {72}^o. cot {18}^o$
bằng

A. -1

B. 1

Đáp án chính xác

C. 0

D. 2

Trả lời:

Chọn B.
 
Ta có:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Nếu tan β2=4tan α2 thì tanβ-α2bằng :
   
   

   Câu hỏi:
   

   Nếu $\tan \frac{\beta }{2}=4\tan \frac{\alpha }{2}$ thì $\tan \frac{\beta –\alpha }{2}$bằng :

   

   Đáp án chính xác

   

   

   

   Trả lời:

   Chọn A.
   Sử dụng công thức cộng ; ta có:
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Biểu thức  có kết quả rút gọn là :
   
   

   Câu hỏi:
   

   Biểu thức 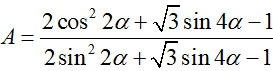 có kết quả rút gọn là :

   

   

   

   Đáp án chính xác

   

   Trả lời:

   Chọn C.
   Áp dụng công thức nhân đôi; ta có :
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Nếu 5sin α = 3sin(α + 2β) thì :
   
   

   Câu hỏi:
   

   Nếu 5sin α = 3sin(α + 2β) thì :

   A. tan(α + β) = 2tan β.

   B. tan(α + β) = 3tan β.

   C. tan(α + β) = 4tan β.

   Đáp án chính xác

   D. tan(α + β) = 5tan β.

   Trả lời:

   Chọn C.
   Áp dụng công thức cộng ; ta có :
   5sin α = 3sin(α + 2β) ⇔ 5sin[(α + β) – β] = 3sin(α + β) + β]
   ⇔ 5sin(α + β)cos β – 5cos(α + β)sin β = 3sin(α + β)cos β + 3cos(α + β)sin β
   ⇔ 2sin(α + β)cos β = 8cos(α + β)sin β
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Biết α+β+γ=π2 và cot α, cot β, cot γ theo thứ tự lập thành một cấp số cộng. Tích số cot α.cot γ  bằng :
   
   

   Câu hỏi:
   

   Biết $\alpha +\beta +\gamma =\frac{\mathrm{\pi }}{2}$ và cot α, cot β, cot γ theo thứ tự lập thành một cấp số cộng. Tích số cot α.cot γ  bằng :

   A. 2

   B. 1

   C. 3

   Đáp án chính xác

   D. 4

   Trả lời:

   Chọn C.
   Ta có : , suy ra 
   
   
   Suy ra :
    ( rút gọn cả 2 vế cho cotβ)
   ⇒ cot α.cot γ =3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC. Hãy chọn hệ thức đúng trong các hệ thức sau.
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Hãy chọn hệ thức đúng trong các hệ thức sau.

   A. cos²A + cos²B + cos²C = 1 + cosA.cosB.cosC

   B. cos²A + cos²B + cos²C = 1 – cosA.cosB.cosC

   C. cos²A + cos²B + cos²C = 1 -2cosA.cosB.cosC

   Đáp án chính xác

   D. cos²A + cos²B + cos²C = 1 – 3cosA.cosB.cosC

   Trả lời:

   Chọn C.
   Sử dụng công thức hạ bậc và biến đổi tổng thành tích  ta có :
   cos²A + cos²B + cos²C 
   = 1 + cos( A + B) .cos( A – B) + cos²C = 1 – cos C. cos( A – B) – cos C.cos( A + B)
   = 1 – cosC[cos (A – B) + cos(A + B) ] = 1 + 2cosA. cosB.cosC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====