Câu hỏi:
Đồ thị hàm số y = 2x2 + 4x – 1 là hình:
A.
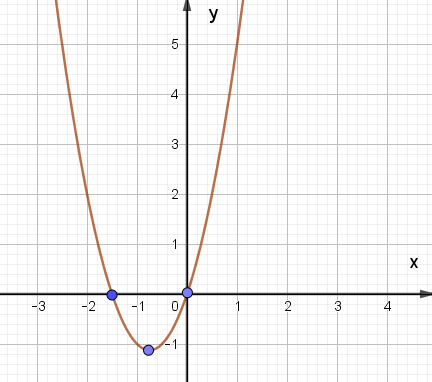
B.
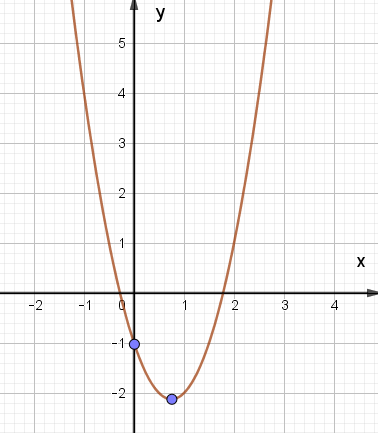
C.
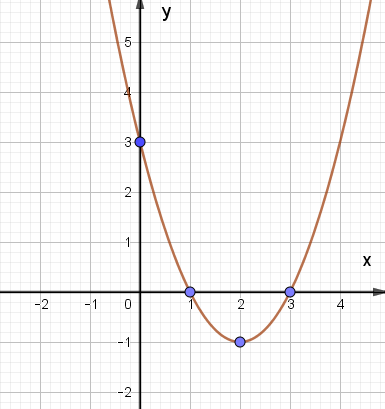
D.
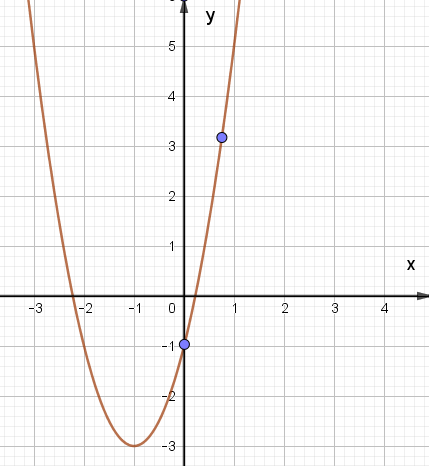
Đáp án chính xác
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số y = 2x2 + 4x – 1, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x2 + 4x – 1 là một parabol (P):
– Có đỉnh S với hoành độ xS = –1, tung độ yS = –3;
– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 2 > 0;
– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1).
Ta vẽ được đồ thị như hình dưới:

====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ đồ thị hàm số: y = f(x) = –x2 + 4x – 3.
Câu hỏi:
Vẽ đồ thị hàm số: y = f(x) = –x2 + 4x – 3.
Trả lời:
Hướng dẫn giải:
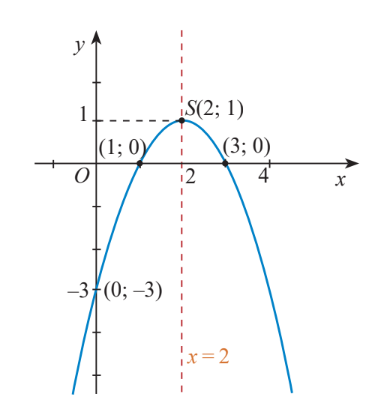
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 4x – 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 1 < 0;
– Cắt trục tung tại điểm có tung độ bằng –3, tức là đồ thị đi qua điểm có tọa độ (0; –3);
Ngoài ra, phương trình –x2 + 4x – 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ đồ thị hàm số y = f(x) = x2 + 2x + 2.
Câu hỏi:
Vẽ đồ thị hàm số y = f(x) = x2 + 2x + 2.
Trả lời:
Hướng dẫn giải:
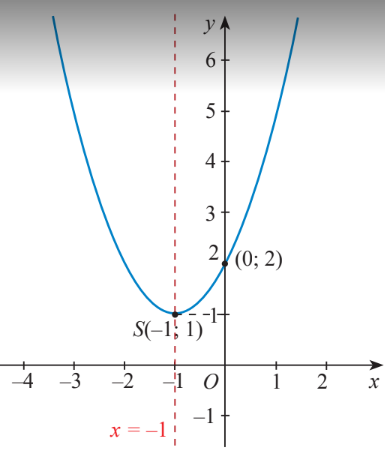
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 + 2x + 2 là một parabol (P):
– Có đỉnh S với hoành độ xS = –1, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2);
Ta vẽ được đồ thị
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số y = x2 – 4x + 3 là parabol có tọa độ đỉnh là:
Câu hỏi:
Đồ thị của hàm số y = x2 – 4x + 3 là parabol có tọa độ đỉnh là:
A. (2; –1);
Đáp án chính xác
B. (4; –1);
C. (2; 0);
D. (4; 0).
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = x2 – 4x + 3 có a = 1, b = –4, c = 3. Đỉnh của parabol có:
Hoành độ: \(\frac{{ – b}}{{2a}} = \frac{{ – ( – 4)}}{{2.1}} = 2\)
Tung độ: \(\frac{{ – \Delta }}{{4a}} = – \frac{{{b^2} – 4ac}}{{4a}} = – \frac{{{{( – 4)}^2} – 4.1.3}}{{4.1}} = – 1\).
Do đó, parabol có tọa độ đỉnh là: (2; –1).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số y = 2×2 + 8x + 1 là parabol có trục đối xứng là:
Câu hỏi:
Đồ thị của hàm số y = 2x2 + 8x + 1 là parabol có trục đối xứng là:
A. x = 2;
B. x = –2;
Đáp án chính xác
C. x = 4;
D. x = – 4.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = 2x2 + 8x + 1 có a = 2, b = 8, c = 1 có trục đối xứng là đường thẳng :
\(x = \frac{{ – b}}{{2a}} = \frac{{ – 8}}{{2.2}} = – 2\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
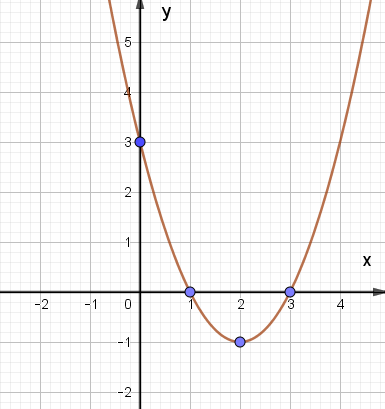
- Đồ thị hàm số y = x2 – 4x + 3 là:
Câu hỏi:
Đồ thị hàm số y = x2 – 4x + 3 là:
A.
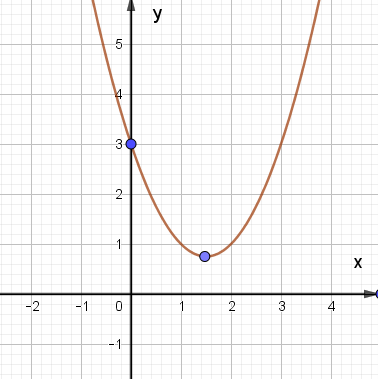
B.
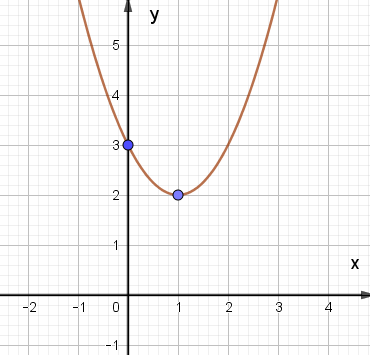
C.
Đáp án chính xác
D.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = f(x) = x2 – 4x + 3, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 – 4x + 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = – 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);
– Ngoài ra, phương trình x2 – 4x + 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị như hình dưới:

====== **** mời các bạn xem câu tiếp bên dưới **** =====