Câu hỏi:
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo, E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \);
Trả lời:
Lời giải
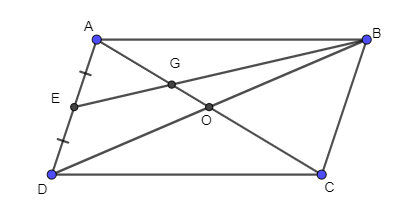
Xét hình bình hành ABCD, có O là giao điểm của AC và BD nên O là trung điểm của AC và O là trung điểm của BD.
⇒ \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) và \(\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \)
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
\( = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\)
\( = \overrightarrow 0 + \overrightarrow 0 \)
\( = \overrightarrow 0 \).
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} – \overrightarrow {NP} = \overrightarrow {MP} \).
B. \( – \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).
C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).
D. \(\overrightarrow {MN} + \overrightarrow {NP} = – \overrightarrow {MP} \).
Câu hỏi:
Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} – \overrightarrow {NP} = \overrightarrow {MP} \).
B. \( – \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).
C. \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \).
D. \(\overrightarrow {MN} + \overrightarrow {NP} = – \overrightarrow {MP} \).Trả lời:
Lời giải
Đáp án đúng là C
Ta có: \(\overrightarrow {MN} – \overrightarrow {NP} = \overrightarrow {MN} + \overrightarrow {PN} = \overrightarrow {MN} + \overrightarrow {MK} = \overrightarrow {MH} \ne \overrightarrow {MP} \) (H, K là điểm thỏa mãn MKHN là hình bình hành). Do đó A sai.
Ta có: \( – \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow {NT} \ne \overrightarrow {MP} \)(T là điểm MNPT là hình bình hành). Do đó B sai
Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \) (quy tắc ba điểm). Do đó C đúng.
Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \ne – \overrightarrow {MP} \). Do đó D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \).
B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \).
C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \).
D. \(\overrightarrow {AB} + \overrightarrow {BC} = – \overrightarrow {AC} \).
Câu hỏi:
Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {CA} \).
B. \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} \).
C. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {CA} \).
D. \(\overrightarrow {AB} + \overrightarrow {BC} = – \overrightarrow {AC} \).Trả lời:
Lời giải
Đáp án đúng là A
Ta có: \(\overrightarrow {BA} + \overrightarrow {DA} = \overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA} \). Do đó A đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \ne \overrightarrow {AD} \). Do đó B sai.
Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \ne \overrightarrow {CA} \). Do đó C sai.
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \ne – \overrightarrow {AC} \). Do đó D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các điểm A, B, O. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} = \overrightarrow {OA} – \overrightarrow {OB} \).
B. \(\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} \).
C. \(\overrightarrow {AB} = \overrightarrow {OA} + \overrightarrow {OB} \).
D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \).
Câu hỏi:
Cho các điểm A, B, O. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} = \overrightarrow {OA} – \overrightarrow {OB} \).
B. \(\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} \).
C. \(\overrightarrow {AB} = \overrightarrow {OA} + \overrightarrow {OB} \).
D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \).Trả lời:
Lời giải
Đáp án đúng là B
Cho các điểm A, B, O. Khẳng định nào sau đây đúng?
Ta có: \(\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {BO} = \overrightarrow {BO} + \overrightarrow {OA} = \overrightarrow {BA} \ne \overrightarrow {AB} \). Do đó A sai.
Ta có: \(\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {OB} + \overrightarrow {AO} = \overrightarrow {AO} + \overrightarrow {OB} = \overrightarrow {AB} \). Do đó B đúng.
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \ne \overrightarrow {AB} \) (C là điểm thỏa mãn OBCA là hình bình hành). Do đó C sai.
Ta có: \(\overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {OC} \ne \overrightarrow {AB} \)(C là điểm thỏa mãn OBCA là hình bình hành). Do đó D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để M là trung điểm của đoạn thẳng AB là:
A. \(\overrightarrow {MA} = \overrightarrow {MB} \).
B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\).
C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng.
D. \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).
Câu hỏi:
Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để M là trung điểm của đoạn thẳng AB là:
A. \(\overrightarrow {MA} = \overrightarrow {MB} \).
B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\).
C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng.
D. \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).Trả lời:
Lời giải
Đáp án đúng là D
M là trung điểm của đoạn thẳng AB thì MA = MB và \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng.
⇒ \(\overrightarrow {MA} = – \overrightarrow {MB} \) hay \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
Vậy điều kiện đủ đề M là trung điểm của đoạn thẳng AB là \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC. Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là:
A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \).
B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \).
C. \(\overrightarrow {GC} + \overrightarrow {GB} = \overrightarrow {GA} \).
D. \(\overrightarrow {GA} + \overrightarrow {GB} – \overrightarrow {GC} = \overrightarrow 0 \).
Câu hỏi:
Cho tam giác ABC. Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là:
A. \(\overrightarrow {GA} + \overrightarrow {GB} = \overrightarrow {GC} \).
B. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \).
C. \(\overrightarrow {GC} + \overrightarrow {GB} = \overrightarrow {GA} \).
D. \(\overrightarrow {GA} + \overrightarrow {GB} – \overrightarrow {GC} = \overrightarrow 0 \).Trả lời:
Lời giải
Đáp án đúng là B
Điều kiện cần và đủ để G là trọng tâm của tam giác ABC là \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
⇔ \(\overrightarrow {GB} + \overrightarrow {GC} = – \overrightarrow {GA} \)
⇔ \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)====== **** mời các bạn xem câu tiếp bên dưới **** =====