Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng: \(\frac{{{\mathop{\rm cosA}\nolimits} }}{{\rm{a}}} + \frac{{{\rm{cosB}}}}{{\rm{b}}} + \frac{{{\rm{cosC}}}}{{\rm{c}}} = \frac{{{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{b}}^{\rm{2}}}{\rm{ + }}{{\rm{c}}^{\rm{2}}}}}{{{\rm{2abc}}}}\).

By 0

Câu hỏi:

Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng: \(\frac{{{\mathop{\rm cosA}\nolimits} }}{{\rm{a}}} + \frac{{{\rm{cosB}}}}{{\rm{b}}} + \frac{{{\rm{cosC}}}}{{\rm{c}}} = \frac{{{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{b}}^{\rm{2}}}{\rm{ + }}{{\rm{c}}^{\rm{2}}}}}{{{\rm{2abc}}}}\).

Trả lời:

Lời giải
Theo định lí côsin: a2 = b2 + c2 – 2bccosA
⇒ cosA = \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} – {{\rm{a}}^2}}}{{2{\rm{bc}}}}\)
⇒ \(\frac{{{\rm{cosA}}}}{{\rm{a}}}\) = \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} – {{\rm{a}}^2}}}{{2{\rm{abc}}}}\).
Tương tự ta có:
\(\frac{{{\rm{cosB }}}}{{\rm{b}}}\) = \(\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} – {{\rm{b}}^2}}}{{2{\rm{abc}}}}\) và \(\frac{{{\rm{cosC}}}}{{\rm{c}}}\) = \(\frac{{{{\rm{a}}^2} + {{\rm{b}}^2} – {{\rm{c}}^2}}}{{2{\rm{abc}}}}\)
Như vậy: \(\frac{{{\mathop{\rm cosA}\nolimits} }}{{\rm{a}}} + \frac{{{\rm{cosB}}}}{{\rm{b}}} + \frac{{{\rm{cosC}}}}{{\rm{c}}}\) = \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} – {{\rm{a}}^2}}}{{2a{\rm{bc}}}}\) + \(\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} – {{\rm{b}}^2}}}{{2{\rm{abc}}}}\) + \(\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} – {{\rm{b}}^2}}}{{2{\rm{abc}}}}\)
⇒ \(\frac{{{\mathop{\rm cosA}\nolimits} }}{{\rm{a}}} + \frac{{{\rm{cosB}}}}{{\rm{b}}} + \frac{{{\rm{cosC}}}}{{\rm{c}}} = \frac{{{{\rm{a}}^{\rm{2}}}{\rm{ + }}{{\rm{b}}^{\rm{2}}}{\rm{ + }}{{\rm{c}}^{\rm{2}}}}}{{{\rm{2abc}}}}\). ( ĐPCM ).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A, B, C, D và O. Số các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là:

    Câu hỏi:

    Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A, B, C, D và O. Số các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là:

    A. 6;

    Đáp án chính xác

    B. 3;

    C. 4;

    D. 2.

    Trả lời:

    Đáp án đúng là: A
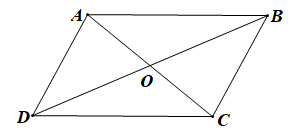
    Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A, B, C, D và O. Số các vectơ khác vectơ - không và cùng phương với vecto AC là: (ảnh 1)
    Các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là: \(\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {AO} ,\overrightarrow {OA} ,\overrightarrow {OC} ,\overrightarrow {CO} .\)
    Vậy có 6 vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} .\)
    Vậy ta chọn phương án A.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Cho đoạn thẳng AC và B là một điểm nằm giữa A, C. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?

    Câu hỏi:

    Cho đoạn thẳng AC và B là một điểm nằm giữa A, C. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?

    A. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) cùng hướng;

    B. Hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {BC} \) cùng hướng;

    C. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng;

    Đáp án chính xác

    D. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BA} \) cùng hướng.

    Trả lời:

    Đáp án đúng là: CVì B nằm giữa A và C nên ta có:• \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) ngược hướng. Do đó phương án A sai.• \(\overrightarrow {CA} \) và \(\overrightarrow {BC} \) ngược hướng. Do đó phương án B sai.• \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng. Do đó phương án C đúng.• \(\overrightarrow {AC} \) và \(\overrightarrow {BA} \) ngược hướng. Do đó phương án D sai.Vậy ta chọn phương án C.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lấy từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} ?\)

    Câu hỏi:

    Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lấy từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} ?\)

    A. 2;

    B. 6;

    C. 4;

    Đáp án chính xác

    D. 8.

    Trả lời:

    Đáp án đúng là: C
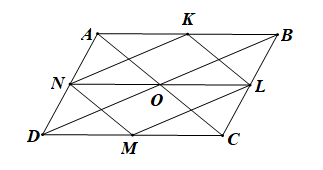
    Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lấy từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ (ảnh 1)
    Vì ABCD là hình bình hành nên AB // CD và AB = CD.
    Lại có K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA
    Nên AK = KB = DM = MC và NL // AB // CD
    Do đó ABLN là hình bình hành (do AB // NL và AN // BL)
    Suy ra AB = NL = CD
    Mà O là tâm hình bình hành nên O là trung điểm của AC và BD
    Do đó đường trung bình NL đi qua O
    Và NO = OL = \(\frac{1}{2}NL = \frac{1}{2}AB = \frac{1}{2}CD\)
    Suy ra AK = KB = NO = OL = DM = MC.
    Khi đó các vectơ bằng vectơ \(\overrightarrow {AK} \) là: \(\overrightarrow {KB} ,\overrightarrow {OL} ,\overrightarrow {DM} ,\overrightarrow {MC} .\)
    Vậy có 4 vectơ bằng vectơ \(\overrightarrow {AK} .\)
    Ta chọn phương án C.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Cho hình thoi ABCD có độ dài các cạnh bằng 1 và \(\widehat {DAB} = 120^\circ .\) Khẳng định nào sau đây là đúng?

    Câu hỏi:

    Cho hình thoi ABCD có độ dài các cạnh bằng 1 và \(\widehat {DAB} = 120^\circ .\) Khẳng định nào sau đây là đúng?

    A. \(\overrightarrow {AB} = \overrightarrow {CD} ;\)

    B. \(\overrightarrow {BD} = \overrightarrow {AC} ;\)

    C. \(\left| {\overrightarrow {BD} } \right| = 1;\)

    D. \(\left| {\overrightarrow {{\rm{AC}}} } \right| = 1.\)

    Đáp án chính xác

    Trả lời:

    Đáp án đúng là: D
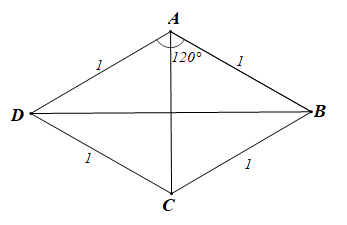
    Cho hình thoi ABCD có độ dài các cạnh bằng 1 và góc DAB = 120^0. Khẳng định nào sau đây là đúng? (ảnh 1)
    • Xét phương án A:
    Vì ABCD là hình thoi nên AB // CD suy ra \(\overrightarrow {AB} = \overrightarrow {DC} .\)
    Do đó phương án A là sai.
    • Xét phương án B:
    Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.
    Khi đó \(\overrightarrow {BD} \bot \overrightarrow {AC} \) nên \(\overrightarrow {BD} \ne \overrightarrow {AC} .\)
    Do đó phương án B là sai.
    • Xét phương án C:
    Vì ABCD là hình thoi có cạnh bằng 1 nên AD = AB = 1.
    Xét ABD có AB = AD = 1 và \(\widehat {DAB} = 120^\circ ,\) áp dụng định lí cosin ta có:
    BD2 = AD2 + AB2 – 2.AD.AB.cos\(\widehat {DAB}\)
    BD2 = 12 + 12 – 2.1.1.cos120°
    BD2 = 3
    BD = \(\sqrt 3 \)
    Khi đó \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt 3 .\)
    Do đó phương án C là sai.
    • Xét phương án D:
    Vì ABCD là hình thoi có cạnh bằng 1 nên AD = CD = 1 .
    Mặt khác \(\widehat {DAB} = 120^\circ \) nên \(\widehat {ADC} = 180^\circ – \widehat {DAB} = 180^\circ – 120^\circ = 60^\circ \)
    Tam giác ADC có AD = DC nên là tam giác cân lại có \(\widehat {ADC} = 60^\circ \)
    Suy ra ADC là tam giác đều
    AC = AD = CD = 1.
    Khi đó \(\left| {\overrightarrow {AC} } \right| = AC = 1.\)
    Do đó phương án D là đúng.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  5. Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài của vectơ \(\overrightarrow {AG} \) bằng

    Câu hỏi:

    Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài của vectơ \(\overrightarrow {AG} \) bằng

    A. \(\sqrt 3 ;\)

    Đáp án chính xác

    B. \(\frac{{3\sqrt 3 }}{2};\)

    C. \(\frac{{\sqrt 3 }}{2};\)

    D. \(2\sqrt 3 .\)

    Trả lời:

    Đáp án đúng là: A
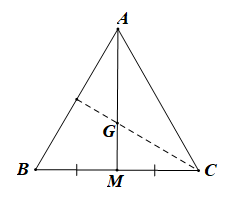
    Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài của vectơ AG bằng (ảnh 1)
    Tam giác ABC đều có cạnh bằng 3 nên AB = AC = 3 và \(\widehat {BAC} = 60^\circ .\)
    Gọi M là trung điểm của BC.
    Khi đó ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
    \( \Rightarrow {\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)^2} = {\left( {2\overrightarrow {AM} } \right)^2}\)
    \( \Rightarrow A{B^2} + 2.\overrightarrow {AB} .\overrightarrow {AC} + A{C^2} = 4A{M^2}\)
    \( \Rightarrow A{B^2} + 2.AB.AC.c{\rm{os}}\widehat {BAC} + A{C^2} = 4A{M^2}\)
    32 + 2.3.3.cos60° + 32 = 4.AM2
    4.AM2 = 27
    AM2 = \(\frac{{27}}{4}\)
    AM = \(\sqrt {\frac{{27}}{4}} = \frac{{3\sqrt 3 }}{2}\)
    Vì G là trọng tâm tam giác ABC nên AG = \(\frac{2}{3}\)AM
    AG = \(\frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 .\)
    Khi đó \(\left| {\overrightarrow {AG} } \right| = AG = \sqrt 3 .\)
    Vậy ta chọn phương án A.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu