Cho tam giác ABC và một điểm M tùy ý. Cho v→=MA→+MB→−2MC→. Hãy xác định vị trí của điểm D sao cho CD→=v→.

Câu hỏi:

Cho tam giác ABC và một điểm M tùy ý. Cho $\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}$. Hãy xác định vị trí của điểm D sao cho $\overrightarrow{CD}=\overrightarrow{v}$.

A. D là điểm thứ tư của hình bình hành ABCD; 

B. D là điểm thứ tư của hình bình hành ACBD;

Đáp án chính xác

C. D là trọng tâm của tam giác ABC;  

D. D là trực tâm của tam giác ABC.

Trả lời:

Hướng dẫn giải
Đáp án đúng là: B
Ta có $\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}=\overrightarrow{MA}-\overrightarrow{MC}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CI}$ (với I là trung điểm AB).
Do đó $\overrightarrow{v}$ không phụ thuộc vào vị trí của điểm M.
Khi đó $\overrightarrow{CD}=\overrightarrow{v}=2\overrightarrow{CI}$.
Suy ra I là trung điểm CD.
Vậy D là điểm thứ tư của hình bình hành ACBD.
Vậy ta chọn đáp án B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài CB→+AB→.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính độ dài $\overrightarrow{CB}+\overrightarrow{AB}$.

   A. $\sqrt{13}$

   B. $2\sqrt{13}$

   Đáp án chính xác

   C. $2\sqrt{3}$

   D. $\sqrt{3}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   
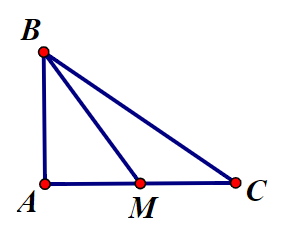
   Gọi M là trung điểm AC, ta suy ra $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0}$.
   $\iff -\overrightarrow{AM}-\overrightarrow{CM}=\overrightarrow{0}$
   $\iff -\left(\overrightarrow{AM}+\overrightarrow{CM}\right)=\overrightarrow{0}$
   $\iff \overrightarrow{AM}+\overrightarrow{CM}=\overrightarrow{0}$
   Ta có $\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{CM}+\overrightarrow{MB}+\overrightarrow{AM}+\overrightarrow{MB}=\left(\overrightarrow{AM}+\overrightarrow{CM}\right)+2\overrightarrow{MB}=\overrightarrow{0}+2\overrightarrow{MB}=2\overrightarrow{MB}$.
   Vì M là trung điểm AC nên AM = $\frac{AC}{2}$ = 2.
   Tam giác ABM vuông tại A: $B{M}^2=A{B}^2+A{M}^2$ (Định lý Pytago)
   $\iff B{M}^2=3^2+2^2=13$
   $\Rightarrow BM=\sqrt{13}$
   Ta suy ra $\left|\overrightarrow{CB}+\overrightarrow{AB}\right|=\left|2\overrightarrow{MB}\right|=2.MB=2\sqrt{13}$.
   Vậy ta chọn đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho a→≠0→ và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn OM→=3a→ và ON→=−4a→. Tìm MN→.
   
   

   Câu hỏi:
   

   Cho $\overrightarrow{a}\ne \overrightarrow{0}$ và điểm O. Gọi M, N lần lượt là hai điểm thỏa mãn $\overrightarrow{OM}=3\overrightarrow{a}$ và $\overrightarrow{ON}=-4\overrightarrow{a}$. Tìm $\overrightarrow{MN}$.

   A. $\overrightarrow{MN}=7\overrightarrow{a}$

   B. $\overrightarrow{MN}=5\overrightarrow{a}$

   C. $\overrightarrow{MN}=–7\overrightarrow{a}$

   Đáp án chính xác

   D. $\overrightarrow{MN}=–5\overrightarrow{a}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   Ta có $\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=-4\overrightarrow{a}-3\overrightarrow{a}=-7\overrightarrow{a}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?
   
   

   Câu hỏi:
   

   Cho tam giác ABC có trọng tâm G. Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Trong các khẳng định sau, khẳng định nào đúng?

   A. $\overrightarrow{AG}=\frac{1}{2}\overrightarrow{AE}+\frac{1}{2}\overrightarrow{\text{AF}}$

   B. $\overrightarrow{AG}=\frac{1}{3}\overrightarrow{AE}+\frac{1}{3}\overrightarrow{\text{AF}}$

   C. $\overrightarrow{AG}=\frac{3}{2}\overrightarrow{AE}+\frac{3}{2}\overrightarrow{\text{AF}}$

   D. $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AE}+\frac{2}{3}\overrightarrow{\text{AF}}$

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   
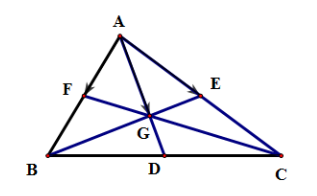
   Vì G là trọng tâm của tam giác ABC nên ta có $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}$.
   Tam giác ABC có D là trung điểm cạnh BC, suy ra $2\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{AC}$.
   Ta có E, F lần lượt là trung điểm AC, AB.
   Suy ra $\overrightarrow{AC}=2\overrightarrow{AE}$ và $\overrightarrow{AB}=2\overrightarrow{AF}$.
   Khi đó ta có $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\frac{1}{3}\left(2\overrightarrow{AF}+2\overrightarrow{AE}\right)=\frac{2}{3}\overrightarrow{AE}+\frac{2}{3}\overrightarrow{AF}$.
   Vậy ta chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho ba điểm phân biệt A, B, C. Nếu AB→=−3AC→ thì đẳng thức nào dưới đây đúng?
   
   

   Câu hỏi:
   

   Cho ba điểm phân biệt A, B, C. Nếu $\overrightarrow{AB}=-3\overrightarrow{AC}$ thì đẳng thức nào dưới đây đúng?

   A. $\overrightarrow{BC}=-4\overrightarrow{AC}$

   B. $\overrightarrow{BC}=-2\overrightarrow{AC}$

   C. $\overrightarrow{BC}=2\overrightarrow{AC}$

   D. $\overrightarrow{BC}=4\overrightarrow{AC}$

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   
   Từ đẳng thức $\overrightarrow{AB}=-3\overrightarrow{AC}$, ta suy ra ba điểm A, B, C thẳng hàng.
   Vì k = – 3 < 0 nên $\overrightarrow{AB}$ và $\overrightarrow{AC}$ ngược hướng. Do đó điểm A nằm giữa hai điểm B và C.
   Ta có $\overrightarrow{AB}=-3\overrightarrow{AC}$, suy ra $\left|\overrightarrow{AB}\right|=\left|-3\overrightarrow{AC}\right|$, do đó AB = 3AC.
   Suy ra BC = AB + AC = 3AC + AC = 4AC.
   Mà $\overrightarrow{BC},\overrightarrow{AC}$ cùng hướng.
   Do đó ta suy ra $\overrightarrow{BC}=4\overrightarrow{AC}$.
   Vậy ta chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?

   A. $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

   B. $\overrightarrow{OA}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{CB}\right)$

   C. $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}+\overrightarrow{OD}$

   Đáp án chính xác

   D. $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{DA}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   
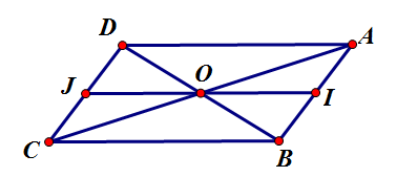
   Ta xét từng đáp án:
   Đáp án A: Theo quy tắc hình bình hành, ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ ⇒ A đúng.
   Đáp án B: Vì O là tâm của hình bình hành ABCD nên O là trung điểm AC.
   Ta suy ra $OA=\frac{1}{2}CA$.
   Mà $\overrightarrow{OA},\overrightarrow{CA}$ cùng hướng.
   Do đó $\overrightarrow{OA}=\frac{1}{2}\overrightarrow{CA}=\frac{1}{2}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)$⇒ B đúng.
   Đáp án C: Gọi I, J lần lượt là trung điểm của AB và CD.
   Ta có $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}$ và $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OJ}$.
   Mà $\overrightarrow{OI},\overrightarrow{OJ}$ là hai vectơ đối nhau.
   Do đó $2\overrightarrow{OI}\ne 2\overrightarrow{OJ}$.
   Suy ra $\overrightarrow{OA}+\overrightarrow{OB}\ne \overrightarrow{OC}+\overrightarrow{OD}$ ⇒ C sai.
   Đáp án D: Ta có OI là đường trung bình của tam giác ABD.
   Suy ra $\overrightarrow{OI}=\frac{1}{2}\overrightarrow{DA}$.
   Ta có $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}=2.\frac{1}{2}\overrightarrow{DA}=\overrightarrow{DA}$ ⇒ D đúng.
   Vậy ta chọn đáp án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====