Câu hỏi:
Cho tam giác ABC thỏa mãn sin2A = sinB. sinC. Hỏi mệnh đề nào đúng.
A. a2 = bc
B. cosA ≥ ½
C. Cả A và B sai
D. Cả A và B đúng
Đáp án chính xác
Trả lời:
Chọn D.
+ Áp dụng định lí sin ta có
Suy ra sin2A = sinB. Sin C khi và chỉ khi :
Hay a2 = bc
+ Áp dụng định lí côsin và ý trên ta có
Vậy cả A và B đúng.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a→(2;-3); b→(5;m). Giá trị của m để 2 vecto cùng phương là:
Câu hỏi:
Cho . Giá trị của m để 2 vecto cùng phương là:
A. -6.
B.
C. 8.
D.
Đáp án chính xác
Trả lời:
Chọn D.
Ta có:
cùng phương suy ra 
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các điểm A(1;1) ; B( 2;4) và C(10; -2) . Góc BAC bằng bao nhiêu độ?
Câu hỏi:
Cho các điểm A(1;1) ; B( 2;4) và C(10; -2) . Góc BAC bằng bao nhiêu độ?
A. 900
Đáp án chính xác
B. 450
C. 1200
D. 300
Trả lời:
Chọn A.
Ta có:
và
Suy ra:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ?
Câu hỏi:
Gọi
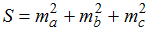là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ?A. S = ¾.( a2 + b2 + c2).
Đáp án chính xác
B. S = a2
C. S = 3/2.( a2 + b2 + c2).
D. S = 3( a2 + b2 + c2).
Trả lời:
Chọn A.
Áp dụng công thức độ dài đuờng trung tuyến ta có
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tam giác ABC có a2 + b2 – c2 > 0. Khi đó :
Câu hỏi:
Cho tam giác ABC có a2 + b2 – c2 > 0. Khi đó :
A. Góc C > 900.
B. Góc C < 900.
Đáp án chính xác
C. Góc C = 900.
D. Không thể kết luận được gì về góc C.
Trả lời:
Chọn B.
Theo hệ quả định lí cosin ta có:
Mà a2 + b2 – c2 > 0 suy ra: cosC > 0 suy ra: C < 900.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Một tam giác có ba cạnh là 52; 56; 60. Bán kính đường tròn ngoại tiếp là:
Câu hỏi:
Một tam giác có ba cạnh là 52; 56; 60. Bán kính đường tròn ngoại tiếp là:
A. 32,5
Đáp án chính xác
B. 32
C. 36
D. Đáp án khác
Trả lời:
Chọn A.
Ta có nửa chu vi của tam giác đã cho là:
P = (52 + 56 + 60) : 2 = 84
Suy ra:
Mà
====== **** mời các bạn xem câu tiếp bên dưới **** =====