Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính CA→−HC→.

Câu hỏi:

Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính $\left|\overrightarrow{CA}-\overrightarrow{HC}\right|$.

A. $\frac{a}{2}$

B. $\frac{3a}{2}$

C. $\frac{2\sqrt{3}a}{3}$

D. $\frac{a\sqrt{7}}{2}$

Đáp án chính xác

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: D.

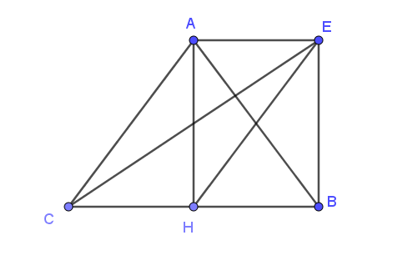
Ta có: $\overrightarrow{CA}-\overrightarrow{HC}=\overrightarrow{CA}+\overrightarrow{CH}$
Dựng hình bình hành CAEH.
Do tam giác ABC đều nên AH vừa là trung tuyến vừa là đường cao.
Do đó, AH vuông góc với BC $\Rightarrow \widehat{AHB}=90°$.
Mà AE // CH (do CAEH là hình bình hành)
Do đó, AH vuông góc với AE $\Rightarrow \widehat{HAE}=90°$.
Vậy AEBH là hình chữ nhật.
Ta có: CH = BH = $\frac{BC}{2}=\frac{a}{2}$ .

Xét tam giác CHA vuông tại H
Áp dụng định lý Pythagore ta có:
AC² = AH² + CH²  ⇔ AH² = AC² – CH²   = $a^2-{\left(\frac{a}{2}\right)}^2=\frac{3a^2}{4}$ ⇒ $AH=\frac{a\sqrt{3}}{2}$.
⇒ $EB=AH=\frac{a\sqrt{3}}{2}$ (do AEBH là hình chữ nhật)
Xét tam giác CBE vuông tại B
Áp dụng định lý Pythagore ta có:
CE² = BC² + BE² = $a^2+{\left(\frac{a\sqrt{3}}{2}\right)}^2=\frac{7}{4}{a}^2$ ⇒ $CE=\frac{a\sqrt{7}}{2}$.
Theo quy tắc hình bình hành:  $\overrightarrow{CA}+\overrightarrow{CH}=\overrightarrow{CE}$.
$\Rightarrow \left|\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|=\left|\overrightarrow{CE}\right|=CE=\frac{a\sqrt{7}}{2}$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình vuông ABCD tâm I, có cạnh bằng a. Tính AB→+AD→.
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD tâm I, có cạnh bằng a. Tính $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|$.

   A. $a\sqrt{2}$;

   Đáp án chính xác

   B. a;

   C. 2a;

   D. $\frac{a}{2}$.

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: A.
   
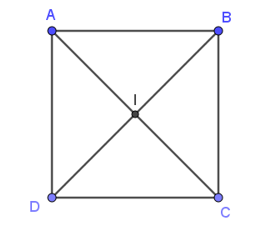
   Áp dụng quy tắc hình bình hành, ta có: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC$.
   Xét tam giác ADC vuông tại D (do ABCD là hình vuông) có:
   Áp dụng định lý Pythagore cho tam giác vuông ACD, ta có:
   AC² = AD² + CD² = a² + a² = 2a²  ⇔ AC = $a\sqrt{2}$
   Vậy $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=a\sqrt{2}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC vuông cân tại A có AB = a. Độ dài của vectơ a→=AB→+AC→ là:
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông cân tại A có AB = a. Độ dài của vectơ $\overrightarrow{a}=\overrightarrow{AB}+\overrightarrow{AC}$ là:

   A. $a\sqrt{2}$;

   Đáp án chính xác

   B. $\frac{a\sqrt{2}}{2}$;

   C. 2a;

   D. a

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: A.
   
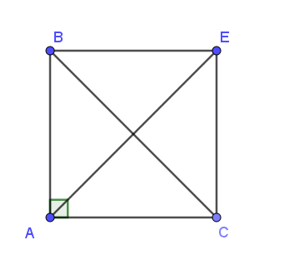
   Vẽ hình bình hành ABEC, theo quy tắc hình bình hành, ta có: $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}$.
   Do ABC là tam giác vuông cân cạnh AB = a nên ABEC là hình vuông cạnh a.
   Xét tam giác ABE vuông tại B
   Áp dụng định lý Pythagore ta có:
   AE² = AB² + BE² = a² + a² = 2a²  ⇔ AE = $a\sqrt{2}$
   Vậy $\left|\overrightarrow{a}\right|=\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{2}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC vuông cân tại C và AB = 2. Tính AB→−AC→.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông cân tại C và AB = $\sqrt{2}$. Tính $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|$.

   A. 3

   B. 1

   Đáp án chính xác

   C. 2

   D. 4

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: B.
   
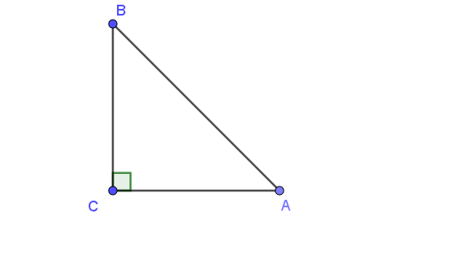
   Ta có: $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\Rightarrow \left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=CB$.
   Xét tam giác ABC vuông tại C
   Áp dụng định lý Pythagore ta có:
   AB² = BC² + CA²
   Mà BC = CA nên BC² = CA² = $\frac{A{B}^2}{2}$=$\frac{{\left(\sqrt{2}\right)}^2}{2}$=1
   ⇔ CB = CA = 1
   Vậy $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|$ = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ u→=CA→+AB→ bằng:
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ $\overrightarrow{u}=\overrightarrow{CA}+\overrightarrow{AB}$ bằng:

   A. 2

   B. $2\sqrt{13}$;

   C. 5

   Đáp án chính xác

   D. $\sqrt{13}$.

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: C.
   
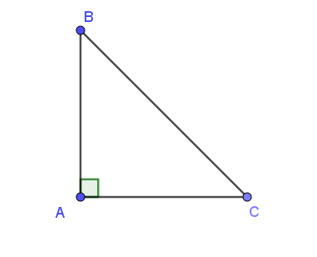
   Xét tam giác ABC vuông tại A
   Áp dụng định lý Pythagore ta có:
   BC² = AB² + AC² = 4² + 3² = 25 ⇔ BC = 5
   Ta có: $\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CB}\Rightarrow \left|\overrightarrow{CA}+\overrightarrow{AB}\right|=\left|\overrightarrow{CB}\right|=CB=5$.
   Vậy $\left|\overrightarrow{u}\right|=5$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC có: AB = AC = a và BAC^=120°. Ta có AB→+AC→ = ?
   
   

   Câu hỏi:
   

   Cho tam giác ABC có: AB = AC = a và $\widehat{BAC}=120°$. Ta có $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|$ = ?

   A. $a\sqrt{3}$;

   B. a;

   Đáp án chính xác

   C. $\frac{a}{2}$;

   D. 2a.

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: B.
   
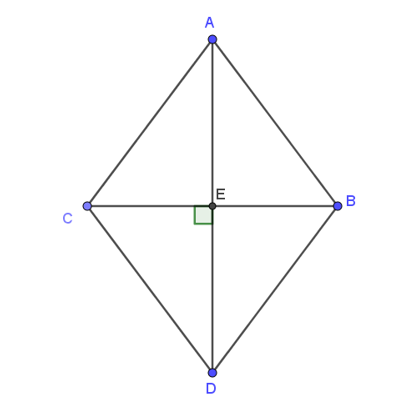
   Dựng hình bình hành ABDC.
   Do tam giác ABC cân có: AB = AC = a nên ABDC là hình thoi cạnh a.
   Gọi E là giao điểm hai đường chéo AD và BC của hình thoi.
   Có $\widehat{BAC}=120°\Rightarrow \widehat{CAE}=60°$ (đường chéo của hình thoi cũng là tia phân giác của các góc ở đỉnh).
   Xét tam giác AEC vuông tại E (do trong hình thoi, hai đường chéo vuông góc với nhau) có:
   $\cos \widehat{CAE}=\frac{AE}{AC}\Rightarrow AE=AC.\cos \widehat{CAE}=a.cos60°=\frac{a}{2}$.
   Lại có: AD = 2AE = $2.\frac{a}{2}=a$.
   Theo quy tắc hình bình hành ta có: $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=AD=a$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====