Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

Câu hỏi:

Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

A. $\overrightarrow{MN}\left(\overrightarrow{NP}+\overrightarrow{PQ}\right)=\overrightarrow{MN}.\overrightarrow{NP}+\overrightarrow{MN}.\overrightarrow{PQ}$

B. $\overrightarrow{MP}.\overrightarrow{MN}=-\overrightarrow{MN}.\overrightarrow{MP}$

Đáp án chính xác

C. $\overrightarrow{MN}.\overrightarrow{PQ}=\overrightarrow{PQ}.\overrightarrow{MN}$

D. $\left(\overrightarrow{MN}-\overrightarrow{PQ}\right)\left(\overrightarrow{MN}+\overrightarrow{PQ}\right)=M{N}^2-P{Q}^2$

Trả lời:

Hướng dẫn giải
Đáp án đúng là: B
Đáp án A đúng theo tính chất phân phối của tích vô hướng.
Đáp án B sai. Sửa lại: $\overrightarrow{MP}.\overrightarrow{MN}=\overrightarrow{MN}.\overrightarrow{MP}$.
Đáp án C đúng theo tính chất giao hoán của tích vô hướng.
Đáp án D đúng theo bình phương vô hướng và hằng đẳng thức.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho 5 điểm M, N, P, Q, R. Tính tổng MN→+PQ→+RN→+NP→+QR→.
   
   

   Câu hỏi:
   

   Cho 5 điểm M, N, P, Q, R. Tính tổng $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}$.

   A. $\overrightarrow{MR}$

   B. $\overrightarrow{MN}$

   Đáp án chính xác

   C. $\overrightarrow{PR}$

   D. $\overrightarrow{MP}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   Ta có $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\left(\overrightarrow{MN}+\overrightarrow{NP}\right)+\left(\overrightarrow{PQ}+\overrightarrow{QR}\right)+\overrightarrow{RN}$.
   $=\overrightarrow{MP}+\overrightarrow{PR}+\overrightarrow{RN}=\overrightarrow{MR}+\overrightarrow{RN}=\overrightarrow{MN}$.
   Vậy ta chọn đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho M, N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ MP→+NP→ bằng vectơ nào?
   
   

   Câu hỏi:
   

   Cho M, N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ $\overrightarrow{MP}+\overrightarrow{NP}$ bằng vectơ nào?

   A. $\overrightarrow{AP}$

   B. $\overrightarrow{BP}$

   Đáp án chính xác

   C. $\overrightarrow{MN}$

   D. $\overrightarrow{MB}+\overrightarrow{NB}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: B
   
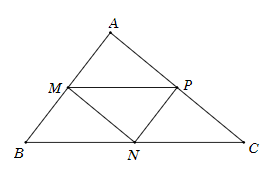
   Tam giác ABC có N, P lần lượt là trung điểm BC và AC.
   Do đó NP là đường trung bình của tam giác ABC.
   Suy ra NP = BM (M là trung điểm AB).
   Mà $\overrightarrow{NP},\overrightarrow{BM}$ cùng hướng.
   Do đó $\overrightarrow{NP}=\overrightarrow{BM}$.
   Ta có $\overrightarrow{MP}+\overrightarrow{NP}=\overrightarrow{MP}+\overrightarrow{BM}=\overrightarrow{BP}$.
   Vậy ta chọn đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm BC. Tính AM→.BC→.
   
   

   Câu hỏi:
   

   Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm BC. Tính $\overrightarrow{AM}.\overrightarrow{BC}$.

   A. $\overrightarrow{AM}.\overrightarrow{BC}=\frac{b^2-c^2}{2}$

   Đáp án chính xác

   B. $\overrightarrow{AM}.\overrightarrow{BC}=\frac{c^2+b^2}{2}$

   C. $\overrightarrow{AM}.\overrightarrow{BC}=\frac{c^2+b^2+a^2}{2}$

   D. $\overrightarrow{AM}.\overrightarrow{BC}=\frac{c^2+b^2-a^2}{2}$

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: A
   Vì M là trung điểm BC nên ta có $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$.
   Khi đó $\overrightarrow{AM}.\overrightarrow{BC}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right).\overrightarrow{BC}=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{AB}\right)\left(\overrightarrow{AC}-\overrightarrow{AB}\right)$ 
   $=\frac{1}{2}\left({\overrightarrow{AC}}^2-{\overrightarrow{AB}}^2\right)=\frac{1}{2}\left(A{C}^2-A{B}^2\right)=\frac{b^2-c^2}{2}$.
   Vậy ta chọn đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Nếu AB→=AC→ thì
   
   

   Câu hỏi:
   

   Nếu $\overrightarrow{AB}=\overrightarrow{AC}$ thì

   A. Tam giác ABC là tam giác cân;

   B. Tam giác ABC là tam giác đều; 

   C. A là trung điểm của đoạn thẳng BC;  

   D. Điểm B trùng với điểm C.

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: D
   $\overrightarrow{AB}=\overrightarrow{AC}\Rightarrow$A, B, C là ba điểm thẳng hàng và B, C nằm cùng phía so với A.
   Mà AB = AC nên B ≡ C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình vuông ABCD tâm O. Tính tổng AB→,  DC→+AD→,  CB→+CO→,  DC→.
   
   

   Câu hỏi:
   

   Cho hình vuông ABCD tâm O. Tính tổng $\left(\overrightarrow{AB},\overrightarrow{DC}\right)+\left(\overrightarrow{AD},\overrightarrow{CB}\right)+\left(\overrightarrow{CO},\overrightarrow{DC}\right)$.

   A. 45°; 

   B. 405°;  

   C. 315°; 

   Đáp án chính xác

   D. 225°.

   Trả lời:

   Hướng dẫn giải
   Đáp án đúng là: C
   
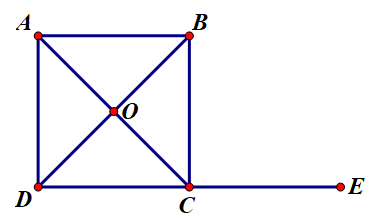
   Ta có $\overrightarrow{AB},\overrightarrow{DC}$ cùng hướng nên $\left(\overrightarrow{AB},\overrightarrow{DC}\right)=0°$.
   Ta có $\overrightarrow{AD},\overrightarrow{CB}$ ngược hướng nên $\left(\overrightarrow{AD},\overrightarrow{CB}\right)=180°$.
   Vẽ $\overrightarrow{CE}=\overrightarrow{DC}$. Khi đó ta có $\left(\overrightarrow{CO},\overrightarrow{DC}\right)=\left(\overrightarrow{CO},\overrightarrow{CE}\right)=\widehat{OCE}$.
   Vì ABCD là hình vuông có OC là đường chéo nên $\widehat{OCB}=45°$.
   Ta có BC ⊥ CD (ABCD là hình vuông)
   Suy ra BC ⊥ CE, do đó $\widehat{BCE}=90°$.
   Ta có $\widehat{OCE}=\widehat{OCB}+\widehat{BCE}=45°+90°=135°$.
   Vậy $\left(\overrightarrow{AB},\overrightarrow{DC}\right)+\left(\overrightarrow{AD},\overrightarrow{CB}\right)+\left(\overrightarrow{CO},\overrightarrow{DC}\right)=0°+180°+135°=315°$.
   Vậy ta chọn đáp án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====