Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Câu hỏi:

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Trả lời:

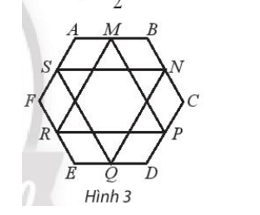
MN là đường trung bình của tam giác ABC nên ta có: $\overrightarrow{\text{MN}}=\frac{1}{2}\overrightarrow{\text{AC}}$.
Tương tự ta có: $\overrightarrow{\text{PQ}}$ = $\frac{1}{2} \overrightarrow{CE}$; $\overrightarrow{RS}=\frac{1}{2} \overrightarrow{EA}$ .
Suy ra $\overrightarrow{MN}+ \overrightarrow{\text{PQ}} +\overrightarrow{RS}=\frac{1}{2}( \overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA})=\frac{1}{2}(\overrightarrow{AE}+ \overrightarrow{EA})= \overrightarrow{0}$
Vậy $\overrightarrow{MN}+ \overrightarrow{\text{PQ}} +\overrightarrow{RS}=\overrightarrow{0}$
Gọi G là trọng tâm tam giác MPR ta có: $\overrightarrow{\text{GM}} + \overrightarrow{\text{GP}}+\overrightarrow{\text{GR}}=\overrightarrow{0}$
Ta lại có:
$\overrightarrow{MN}=\overrightarrow{MG}+\overrightarrow{GN} ; \overrightarrow{PQ}=\overrightarrow{PQ}+\overrightarrow{GQ} ; \overrightarrow{RS}= \overrightarrow{RG}+ \overrightarrow{GS}$
Suy ra $\overrightarrow{MN}+ \overrightarrow{PQ}+\overrightarrow{RS}=\overrightarrow{MG}+ \overrightarrow{GN}+\overrightarrow{PG}+\overrightarrow{GQ}+\overrightarrow{RG}+\overrightarrow{GS}$
$=\overrightarrow{MG}+\overrightarrow{PG}+ \overrightarrow{RG}+ \overrightarrow{GN}+ \overrightarrow{GQ}+\overrightarrow{GS}=\overrightarrow{0}$
Mà $\overrightarrow{GM}+\overrightarrow{GP}+ \overrightarrow{GR}=\overrightarrow{0}$ ⇒  $– (\overrightarrow{GM}+ \overrightarrow{GP}+ \overrightarrow{GR})= \overrightarrow{0}$⇒ $\overrightarrow{MG}+\overrightarrow{PG}+\overrightarrow{RG}= \overrightarrow{0}$.
Do đó $\overrightarrow{GN}+ \overrightarrow{GQ}+ \overrightarrow{GS}= \overrightarrow{0}$
Suy ra G là trọng tâm của tam giác NQS.
Như vậy hai tam giác MPR và NQS có cùng trọng tâm.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình bình hành ABCD có G là trọng tâm tam giác ABD. Chứng minh rằng: AC→=3AG→.
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD có G là trọng tâm tam giác ABD. Chứng minh rằng: $\overrightarrow{\text{AC}}=3\overrightarrow{\text{AG}}$.

   Trả lời:

   

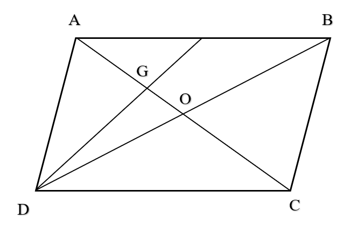
   Gọi O là giao điểm của AC và BD. Khi đó $\overrightarrow{\text{AO}}$ = $\frac{1}{2} \overrightarrow{\text{AC}}$.
   G là trọng tâm tam giác ABD ⇒ $\overrightarrow{\text{AG}}$ = $\frac{2}{3}\overrightarrow{\text{AO}}$.
   Vậy $\overrightarrow{\text{AG}}$ = $\frac{2}{3}$.$\frac{1}{2}$$\overrightarrow{\text{AC}}$ = $\frac{1}{3}\overrightarrow{\text{AC}}$ hay $\overrightarrow{\text{AC}}=3\overrightarrow{\text{AG}}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng: a) 2DA→+DB→+DC→=0→;
   
   

   Câu hỏi:
   

   Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:
   a) $2\overrightarrow{\text{DA}}+\overrightarrow{\text{DB}}+\overrightarrow{\text{DC}}=\overrightarrow{0}$;

   Trả lời:

   
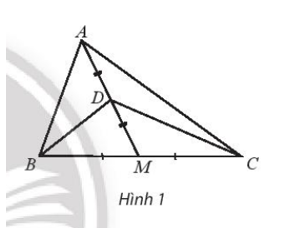
   a) Vì M là trung điểm của BC nên: $\overrightarrow{\text{DB}}+\text{}\overrightarrow{\text{DC}}=2\overrightarrow{\text{DM}}$.
   Mặt khác do D là trung điểm đoạn AM nên $\overrightarrow{\text{DM}}=-\overrightarrow{\text{DA}}\text{}$
   Vậy nên $\overrightarrow{\text{DB}}$ + $\overrightarrow{\text{DC}}$ = –2$\overrightarrow{\text{DA}}$ hay $2\overrightarrow{\text{DA}}+\overrightarrow{\text{DB}}+\overrightarrow{\text{DC}}=2\overrightarrow{\text{DA}}-2\overrightarrow{\text{DA}}=\overrightarrow{0}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) 2OA→+OB→+OC→=4OD→, với O là điểm tùy ý.
   
   

   Câu hỏi:
   

   b) $2\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}}=4\overrightarrow{\text{OD}}$, với O là điểm tùy ý.

   Trả lời:

   

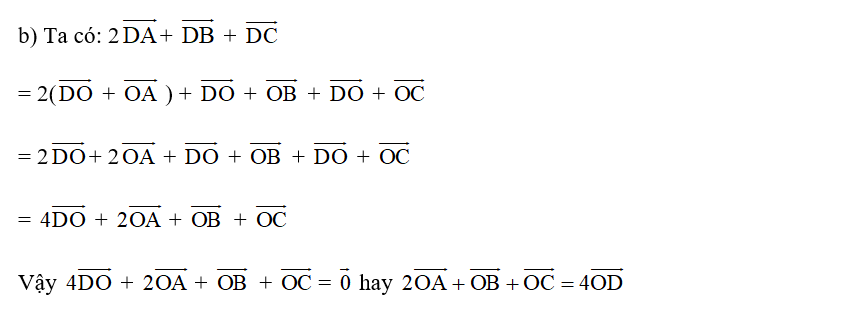
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Lấy một điểm M tùy ý. Chứng minh rằng: a) I là trung điểm của đoạn thẳng AB khi và chỉ khi MA→+MB→=2MI→.
   
   

   Câu hỏi:
   

   Lấy một điểm M tùy ý. Chứng minh rằng:
   a) I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{\text{MA}}+\overrightarrow{\text{MB}}=2\overrightarrow{\text{MI}}$.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. b) G là trọng tâm của tam giác ABC khi và chỉ khi MA→+MB→+MC→=3MG→.
   
   

   Câu hỏi:
   

   b) G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{\text{MA}}+\overrightarrow{\text{MB}}+\overrightarrow{\text{MC}}=3\overrightarrow{\text{MG}}$.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====