Cho hình thang cân ABCD Nhận xét nào sau đây đúng về cặp vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \)?

Câu hỏi:

Cho hình thang cân ABCD

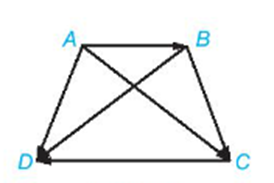
Nhận xét nào sau đây đúng về cặp vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \)?

A. \(\overrightarrow {AB} = \overrightarrow {BD} \);

B. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng phương;

C. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng hướng;

D. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng độ dài.

Đáp án chính xác

Trả lời:

Đáp án đúng là D
Vì AC và BD cắt nhau nên hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không cùng phương. Suy ra hai vec tơ này không cùng hướng và không bằng nhau. Do đó A, B, C sai.
Vì ABCD là hình thang cân nên AC = BD (hai đường chéo bằng nhau). Do đó D đúng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình vẽ sau: Cặp vectơ nào cùng hướng?
   
   

   Câu hỏi:
   

   Cho hình vẽ sau:
   

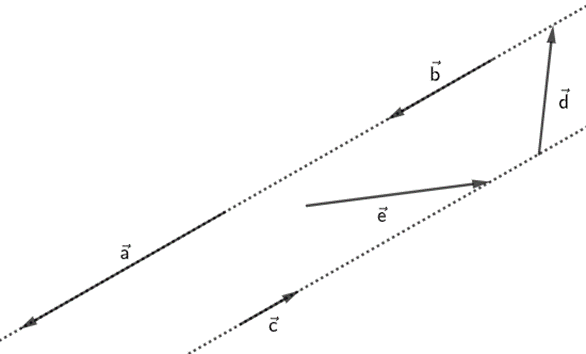
   Cặp vectơ nào cùng hướng?

   A. \(\overrightarrow a \) và \(\overrightarrow b \);

   Đáp án chính xác

   B. \(\overrightarrow a \) và \(\overrightarrow c \);

   C. \(\overrightarrow c \) và \(\overrightarrow b \);

   D. \(\overrightarrow c \) và \(\overrightarrow e \).

   Trả lời:

   Đáp án đúng là A
   Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng nằm trên một đường thẳng hay chúng có giá trùng nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng phương. Do đó hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
   Hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \) nằm trên hai đường thẳng song song hay chúng có giá song song nhau nên \(\overrightarrow a \) và \(\overrightarrow c \) là hai vectơ cùng phương. Do đó hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \) ngược hướng.
   Hai vectơ \(\overrightarrow b \) và \(\overrightarrow c \) nằm trên hai đường thẳng song song hay chúng có giá song song nhau nên \(\overrightarrow b \) và \(\overrightarrow c \) là hai vectơ cùng phương. Do đó hai vectơ \(\overrightarrow b \) và \(\overrightarrow c \) ngược hướng.
   Hai vectơ \(\overrightarrow e \) và \(\overrightarrow c \) không cùng phương.
   Vậy các cặp vec tơ cùng hướng là \(\overrightarrow a \) và \(\overrightarrow b \).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
   
   

   Câu hỏi:
   

   Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
   

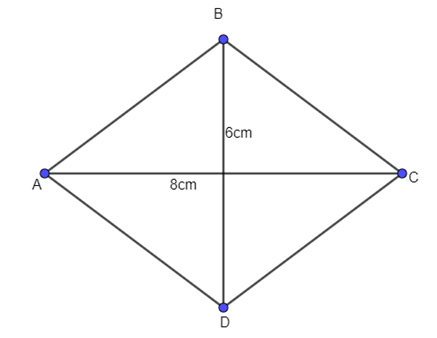
   A. 10 cm;

   Đáp án chính xác

   B. 3 cm;

   C. 4 cm;

   D. 5cm.

   Trả lời:

   Đáp án đúng là D
   

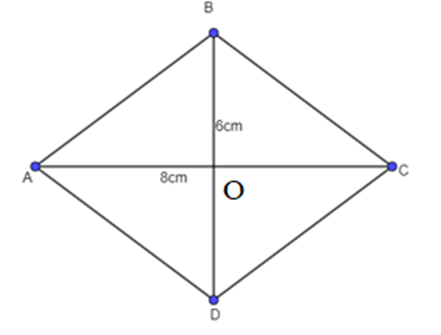
   Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC, cũng là trung điểm của BD.
   ⇒ AO = OC = \(\frac{{AC}}{2} = \frac{8}{2} = 4cm.\)
   ⇒ BO = OD = \(\frac{{BD}}{2} = \frac{6}{2} = 3cm.\)
   Xét tam giác AOB vuông tại O, có:
   AB² = AO² + BO² (định lí Py – ta – go)
   ⇔ AB² = 4² + 3² = 16 + 9 = 25
   ⇔ AB = 5 (cm)
   \( \Rightarrow \left| {\overrightarrow {AB} } \right| = AB = 5cm.\)
   Vậy độ dài \(\overrightarrow {AB} \) là 5cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).

   A. \(\overrightarrow {DC} \);

   B. \(\overrightarrow {AD} \);

   C. \(\overrightarrow {CB} \);

   D. \(\overrightarrow {BA} \).

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là D
   Vì ABCD là hình bình hành nên AB // CD nên \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng phương. Do đó \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng hướng.
   Mặt khác AB = CD (tính chất hình bình hành)
   Suy ra \(\overrightarrow {BA} = \overrightarrow {CD} \).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC. Phát biểu nào dưới đây là sai.
   
   

   Câu hỏi:
   

   Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
   

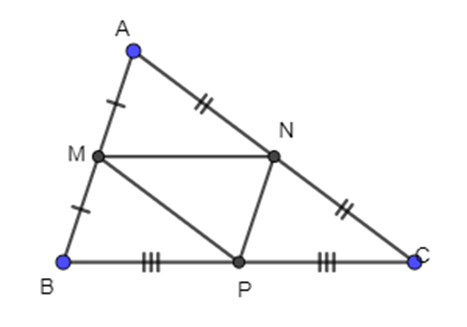
   Phát biểu nào dưới đây là sai.

   A. \(\overrightarrow {MN} = \overrightarrow {PC} \);

   B. \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \);

   C. \(\overrightarrow {MB} = \overrightarrow {AM} \);

   D. \(\overrightarrow {MN} = \overrightarrow {PB} \).

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là D
   +) Xét tam giác ABC, có:
   M là trung điểm AB
   N là trung điểm của AC
   ⇒ MN là đường trung bình của tam giác ABC
   ⇒ MN // BC và MN = \(\frac{1}{2}\)BC
   Mà BP = PC = \(\frac{1}{2}\)BC (P là trung điểm của BC)
   ⇒ MN = CP = PB (1)
   Vì MN // BC nên MN // CP. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng phương. Suy ra \(\overrightarrow {MN} \) và \(\overrightarrow {PC} \) cùng hướng (2)
   Từ (1) và (2) suy ra \(\overrightarrow {MN} \) = \(\overrightarrow {CP} \). Do đó đáp án A đúng.
   Tương tự MN //BC hay MN // PB. Khi đó \(\overrightarrow {MN} \) và \(\overrightarrow {PB} \) cùng phương nhưng ngược hướng (3)
   Từ (1) và (3) suy ra \(\overrightarrow {MN} \) không bằng \(\overrightarrow {PB} \). Do đó đáp án D sai.
   +) Ta có \(\overrightarrow {AA} \) và \(\overrightarrow {PP} \) là các vectơ – không.
   Mà mọi vectơ – không có cùng độ dài và cùng hướng nên bằng nhau
   Suy ra \(\overrightarrow {AA} \) cùng hướng với \(\overrightarrow {PP} \). Do đó đáp án B đúng.
   +) Hai vec tơ \(\overrightarrow {AM} \) và \(\overrightarrow {MB} \) cùng hướng
   Vì M là trung điểm của AB nên AM = MB
   Suy ra \(\overrightarrow {AM} = \overrightarrow {MB} \). Do đó đáp án C đúng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
   
   

   Câu hỏi:
   

   Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.

   A. \(\left| {\overrightarrow {AM} } \right| = \sqrt {53} \)cm

   B. \(\left| {\overrightarrow {AM} } \right| = 3\) cm

   C. \(\left| {\overrightarrow {AM} } \right| = \frac{{\sqrt {53} }}{2}\) cm

   Đáp án chính xác

   D. \(\left| {\overrightarrow {AM} } \right| = \frac{3}{2}\) cm

   Trả lời:

   Đáp án đúng là C
   

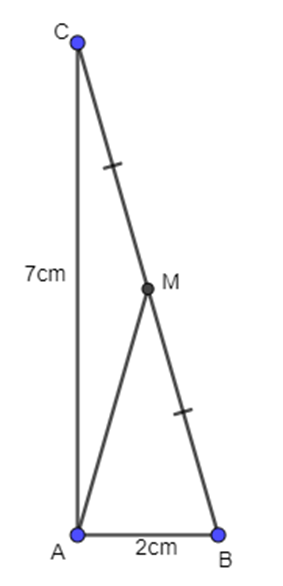
   Xét tam giác ABC vuông tại A, có:
   BC² = AB² + AC² (định lí Py – ta – go)
   ⇔ BC² = 2² + 7² = 4 + 49 = 53
   ⇔ BC = \(\sqrt {53} \) cm
   Ta lại có M là trung điểm BC
   ⇒ AM = \(\frac{1}{2}\) BC (tính chất đường trung tuyến)
   ⇒ AM = \(\frac{{\sqrt {53} }}{2}\) cm.
   ⇒ \(\left| {\overrightarrow {AB} } \right| = AB = \frac{{\sqrt {53} }}{2}cm\)
   Vậy độ dài vectơ \(\overrightarrow {AB} \) là \(\frac{{\sqrt {53} }}{2}cm.\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====