Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính: a) AB→.AO→ ; b) AB→.AD→ .

Câu hỏi:

Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:
a) $\vec{A B} . \vec{A O}$ ;
b) $\vec{A B} . \vec{A D}$ .

Trả lời:

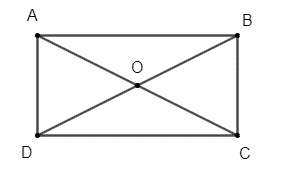
Media VietJack

Vì ABCD là hình chữ nhật nên BC = AD = a, CD = AB = 2a, hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
Áp dụng định lí Pythagore cho tam giác vuông ABC ta có:
AC² = AB² + BC² = (2a)² + a² = 5a² $\Rightarrow A C = a \sqrt{5}$ .
Do đó: $B D = A C = a \sqrt{5}$ .
Suy ra: $A O = \frac{1}{2} A C = \frac{1}{2} . a \sqrt{5} = \frac{a \sqrt{5}}{2}$ .
Ta có: $co s \hat{B A O} = co s \hat{B A C} = \frac{A B}{A C} = \frac{2 a}{a \sqrt{5}} = \frac{2}{\sqrt{5}}$ .
a) $\vec{A B} . \vec{A O} = | \vec{A B} | . | \vec{A O} | . c o s (\vec{A B}, \vec{A O})$ $= A B . A O . \cos \hat{B A O}$ $= 2 a . \frac{a \sqrt{5}}{2} . \frac{2}{\sqrt{5}} = 2 a^{2}$ .
b) $\vec{A B} . \vec{A D} = | \vec{A B} | . | \vec{A D} | . c o s (\vec{A B}, \vec{A D})$ $= A B . A D . c o s \hat{B A D}$ = 2a . a . cos90° = 0.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Trong vật lí, nếu có một lực F→ tác động lên một vật tại điểm O và làm cho vật đó di chuyển một quãng đường s = OM (Hình 63) thì công A của lực F→ được tính theo công thức A=F→ . OM→ . cosφ trong đó F→ gọi là cường độ của lực F→ tính bằng Newton (N), OM→ là độ dài của vectơ OM→ tính bằng mét (m), φ là góc giữa hai vectơ OM→ và F→ , còn công A tính bằng Jun (J). Trong toán học, giá trị của biểu thức A=F→ . OM→ . cosφ (không kể đơn vị đo) được gọi là gì?

Câu hỏi:

Trong vật lí, nếu có một lực $\vec{F}$ tác động lên một vật tại điểm O và làm cho vật đó di chuyển một quãng đường s = OM (Hình 63) thì công A của lực $\vec{F}$ được tính theo công thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ trong đó $|\vec{F}|$ gọi là cường độ của lực $\vec{F}$ tính bằng Newton (N), $|\vec{O M}|$ là độ dài của vectơ $\vec{O M}$ tính bằng mét (m), φ là góc giữa hai vectơ $\vec{O M}$ và $\vec{F}$ , còn công A tính bằng Jun (J).

Trong toán học, giá trị của biểu thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ (không kể đơn vị đo) được gọi là gì?

Trả lời:

Giá trị của biểu thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ là tích vô hướng của hai vectơ $\vec{F}$ và $\vec{O M}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho tam giác ABC vuông tại A có B^=30° , AB = 3 cm. Tính BA→. BC→; CA→. CB→ .

Câu hỏi:

Cho tam giác ABC vuông tại A có $\hat{B} = 30 °$ , AB = 3 cm. Tính $\vec{B A} . \vec{B C}; \vec{C A} . \vec{C B}$ .

Trả lời:

Ta có tam giác ABC vuông ở A nên $\hat{B} + \hat{C} = 90 °$
$\Rightarrow \hat{C} = 90 ° - \hat{B} = 90 ° - 30 ° = 60 °$ .
Lại có: tan B = $\frac{A C}{A B}$ ⇒ AC = AB . tanB = 3 . tan 30° = $\sqrt{3}$ .
Và sin B = $\frac{A C}{B C}$ ⇒ BC = $\frac{A C}{\sin B}$ $= \frac{\sqrt{3}}{\sin 30 °} = 2 \sqrt{3}$ .
Ta có: $\vec{B A} . \vec{B C} =$ $|\vec{B A}| . |\vec{B C}| . \cos (\vec{B A}, \vec{B C})$ = $3 . 2 \sqrt{3} . \cos \hat{A B C}$ = $6 \sqrt{3} . \cos 30 ° = 9$ .
$\vec{C A} . \vec{C B}$ = $|\vec{C A}| . |\vec{C B}| . \cos (\vec{C A}, \vec{C B})$ = $\sqrt{3} . 2 \sqrt{3} . \cos \hat{A C B}$ = 6 . cos 60° = 3.

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính: a) CB→ . BA→ ; b) AH→ . BC→ .

Câu hỏi:

Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) $\vec{C B} . \vec{B A}$ ;
b) $\vec{A H} . \vec{B C}$ .

Trả lời:

a) Tam giác ABC đều nên $\hat{A} = \hat{B} = \hat{C} = 60 °$ và AB = BC = AC = a.
Lại có: $(\vec{B C}, \vec{B A}) = \hat{A B C} = 60 °$ .
Ta có: $\vec{C B} . \vec{B A} = (- \vec{B C}) . \vec{B A}$ $= - (\vec{B C} . \vec{B A})$
$= - (|\vec{B C}| . |\vec{B A}| . \cos (\vec{B C}, \vec{B A}))$
$= - (a . a . \cos 60 °) = \frac{- a^{2}}{2}$ .
Vậy $\vec{C B} . \vec{B A} = \frac{- a^{2}}{2}$ .
b) Do AH là đường cao của tam giác ABC nên AH ⊥ BC.
Do đó: $\vec{A H} ⊥ \vec{B C}$ nên $\vec{A H} . \vec{B C} = 0$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Chứng minh rằng với hai vectơ bất kì a→, b→ , ta có: a→+b→2=a→2+2a→.b→+b→2 a→−b→2=a→2−2a→.b→+b→2 a→−b→.a→+b→=a→2−b→2

Câu hỏi:

Chứng minh rằng với hai vectơ bất kì $\vec{a}, \vec{b}$ , ta có: ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$
${(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$
$(\vec{a} - \vec{b}) . (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2}$

Trả lời:

+ Ta có:
           ${(\vec{a} + \vec{b})}^{2} = (\vec{a} + \vec{b}) . (\vec{a} + \vec{b})$ (bình phương vô hướng của vectơ )
$= \vec{a} . \vec{a} + \vec{a} . \vec{b} + \vec{b} . \vec{a} + \vec{b} . \vec{b}$

         $= {\vec{a}}^{2} + \vec{a} . \vec{b} + \vec{a} . \vec{b} + {\vec{b}}^{2}$ (áp dụng tính chất giao hoán)
$= {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$
Vậy ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ .
+ Ta có:
           ${(\vec{a} - \vec{b})}^{2} = (\vec{a} - \vec{b}) . (\vec{a} - \vec{b})$ (bình phương vô hướng của vectơ )
$= \vec{a} . \vec{a} - \vec{a} . \vec{b} - \vec{b} . \vec{a} + (- \vec{b}) . (- \vec{b})$

          $= {\vec{a}}^{2} - \vec{a} . \vec{b} - \vec{a} . \vec{b} + {\vec{b}}^{2}$ (áp dụng tính chất giao hoán)
$= {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$
Vậy ${(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ .
+ Ta có: $(\vec{a} - \vec{b}) (\vec{a} + \vec{b})$ $= \vec{a} . \vec{a} + \vec{a} . \vec{b} + (- \vec{b}) . \vec{a} + (- \vec{b}) . \vec{b}$
     $= {\vec{a}}^{2} + \vec{a} . \vec{b} - \vec{a} . \vec{b} - \vec{b} . \vec{b}$ (áp dụng tính chất giao hoán)
$= {\vec{a}}^{2} - {\vec{b}}^{2}$ .
Vậy $(\vec{a} - \vec{b}) . (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Sử dụng tích vô hướng, chứng minh minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC2 = AB2 + AC2.

Câu hỏi:

Sử dụng tích vô hướng, chứng minh minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC² = AB² + AC².

Trả lời:

+ Ta chứng minh định lí thuận:
Có tam giác ABC vuông ở A, cần chứng minh BC² = AB² + AC².

Tam giác ABC vuông tại A nên $\hat{B A C} = 90 °$ .
Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$
Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$
                    = AB² + AC² – 2 . AC . AB . cosA
                    = AB² + AC² – 2 . AC . AB . cos 90°
                    = AB² + AC² – 2 . AC . AB . 0
                    = AB² + AC².
Vậy BC² = AB² + AC².
+ Ta chứng minh định lí đảo:
Cho tam giác ABC có BC² = AB² + AC² thì tam giác ABC vuông tại A.

Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$
Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$     (*)
Mà theo giả thiết ta có: BC² = AB² + AC² nên thay vào (*) ta được:
BC² = BC² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$
Suy ra: 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$ = 0
$\Leftrightarrow \cos (\vec{A C}, \vec{A B}) = 0$ hay $\cos \hat{B A C} = 0$
Do đó: $\hat{B A C} = 90 °$ .
Vậy tam giác ABC vuông tại A.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Bài liên quan:

Leave a Comment Hủy