Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng: a) MA→+MB→+MC→+MD→=4MO→; b) AB→+AC→+AD→=2AC→.

Câu hỏi:

Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
a) $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}$;
b) $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AC}$.

Trả lời:

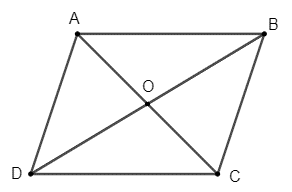
a) O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Khi đó: $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0},\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$.
Theo quy tắc ba điểm, ta có: $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}$
$=(\overrightarrow{MO}+\overrightarrow{OA})+(\overrightarrow{MO}+\overrightarrow{OB})+(\overrightarrow{MO}+\overrightarrow{OC})+(\overrightarrow{MO}+\overrightarrow{OD})$
$=4\overrightarrow{MO}+(\overrightarrow{OA}+\overrightarrow{OC})+(\overrightarrow{OB}+\overrightarrow{OD})$
$=4\overrightarrow{MO}+\overrightarrow{0}+\overrightarrow{0}=4\overrightarrow{MO}$
Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}$.
b) ABCD là hình bình hành nên theo quy tắc hình bình hành ta có: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.
Khi đó ta có:
$\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=(\overrightarrow{AB}+\overrightarrow{AD})+\overrightarrow{AC}=\overrightarrow{AC}+\overrightarrow{AC}=2\overrightarrow{AC}$.
Vậy $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AC}$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho vectơ a→. Hãy xác định độ dài và hướng của hai vectơ a→+a→,  (−a→)+(−a→)   (Hình 1).
   
   

   Câu hỏi:
   

   Cho vectơ $\overrightarrow{a}$. Hãy xác định độ dài và hướng của hai vectơ $\overrightarrow{a}+\overrightarrow{a},(-\overrightarrow{a})+(-\overrightarrow{a})$   (Hình 1).
   

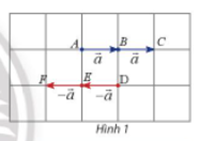
   Trả lời:

   +) Ta có: $AB=\left|\overrightarrow{AB}\right|=\left|\overrightarrow{a}\right|$; $BC=\left|\overrightarrow{BC}\right|=\left|\overrightarrow{a}\right|$
   AC = AB + BC = $\left|\overrightarrow{a}\right|+\left|\overrightarrow{a}\right|=2.\left|\overrightarrow{a}\right|$
   Có: $\overrightarrow{a}+\overrightarrow{a}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
   Do đó: $|\overrightarrow{a}+\overrightarrow{a}|=\left|\overrightarrow{AC}\right|\text{\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}A}C=2.\left|\overrightarrow{a}\right|$.
   Vậy vectơ $\overrightarrow{a}+\overrightarrow{a}$ có độ dài là $2.\left|\overrightarrow{a}\right|$ và có cùng hướng với vectơ $\overrightarrow{a}$ (theo hướng đi từ trái qua phải).
   +) Ta có: $DE=\left|\overrightarrow{DE}\right|=|-\overrightarrow{a}|=\left|\overrightarrow{a}\right|$; $EF=\left|\overrightarrow{EF}\right|=|-\overrightarrow{a}|=\left|\overrightarrow{a}\right|$
   DF = DE + EF = $\left|\overrightarrow{a}\right|+\left|\overrightarrow{a}\right|=2.\left|\overrightarrow{a}\right|$
   Có: $(-\overrightarrow{a})+(-\overrightarrow{a})=\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{DF}$
   Do đó: $|(-\overrightarrow{a})+(-\overrightarrow{a})|=\left|\overrightarrow{DF}\right|=DF=2.\left|\overrightarrow{a}\right|$.
   Vậy vectơ $(-\overrightarrow{a})+(-\overrightarrow{a})$ có độ dài là $2.\left|\overrightarrow{a}\right|$ và ngược hướng với vectơ $\overrightarrow{a}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
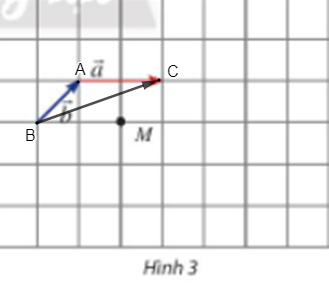
2. Cho hai vectơ a→, b→ và một điểm M như Hình 3. a) Hãy vẽ các vectơ MN→=3a→,  MP→=−3b→. b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: |3b→|,  |−3b→|,  |2a→+2b→|.
   
   

   Câu hỏi:
   

   Cho hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ và một điểm M như Hình 3.
   

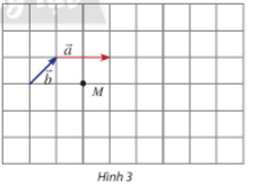
   a) Hãy vẽ các vectơ $\overrightarrow{MN}=3\overrightarrow{a},\overrightarrow{MP}=-3\overrightarrow{b}$.
   b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: $\left|3\overrightarrow{b}\right|,|-3\overrightarrow{b}|,|2\overrightarrow{a}+2\overrightarrow{b}|$.

   Trả lời:

   a) Ta có: $\overrightarrow{MN}=3\overrightarrow{a}$ nên vectơ $\overrightarrow{MN}$ cùng hướng với vectơ $\overrightarrow{a}$ và có độ dài bằng $3.\left|\overrightarrow{a}\right|$.
   Qua M ta vẽ đường thẳng song song với giá của vectơ $\overrightarrow{a}$ và lấy điểm N trên đường thẳng đó cùng hướng với vectơ $\overrightarrow{a}$ thỏa mãn MN = $3.\left|\overrightarrow{a}\right|$.
   Lại có: $\overrightarrow{MP}=-3\overrightarrow{b}$ nên vectơ $\overrightarrow{MP}$ ngược hướng với vectơ $\overrightarrow{b}$ và có độ dài bằng $|-3|.\left|\overrightarrow{b}\right|=3.\left|\overrightarrow{b}\right|$.
   Qua M ta vẽ đường thẳng song song với giá của vectơ $\overrightarrow{b}$ và lấy điểm P trên đường thẳng đó ngược hướng với vectơ $\overrightarrow{b}$ thỏa mãn $MP=3.\left|\overrightarrow{b}\right|$.
   

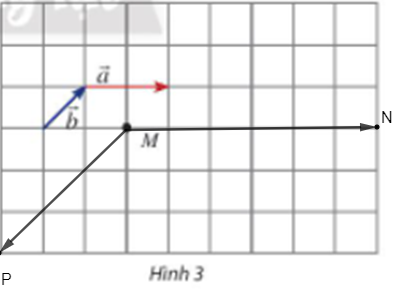
   b) Mỗi ô vuông có cạnh bằng 1 nên đường chéo của mỗi ô vuông có độ dài là $\sqrt{2}$.
   Ta có vectơ $\overrightarrow{a}$ có độ dài là $\left|\overrightarrow{a}\right|=2$, vectơ $\overrightarrow{b}$ có độ dài là $\left|\overrightarrow{b}\right|=\sqrt{2}$.
   Ta có: $\left|3\overrightarrow{b}\right|=3.\left|\overrightarrow{b}\right|=3.\sqrt{2}=3\sqrt{2}$; $|-3\overrightarrow{b}|=|-3|.\left|\overrightarrow{b}\right|=3\sqrt{2}$.
   Lại có: $2\overrightarrow{a}+2\overrightarrow{b}=2(\overrightarrow{a}+\overrightarrow{b})$   (1).
   Ta kí hiệu như hình vẽ dưới với $\overrightarrow{b}=\overrightarrow{BA},\overrightarrow{a}=\overrightarrow{AC}$.
   

   Ta có: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}+\overrightarrow{BA}=\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$   (2).
   Từ (1) và (2) suy ra: $2\overrightarrow{a}+2\overrightarrow{b}=2\overrightarrow{BC}$.
   Nên $|2\overrightarrow{a}+2\overrightarrow{b}|=\left|2\overrightarrow{BC}\right|=2\left|\overrightarrow{BC}\right|=2BC$.
   Ta có: $\widehat{BAC}=45°+90°=135°$ 
   Áp dụng định lí côsin trong tam giác ABC ta có:
   BC² = AB² + AC² – 2 . AB . AC . cosA
           = ${\left(\sqrt{2}\right)}^2$ + 2² – 2 . $\sqrt{2}$ . 2 . cos135° = 10
   Suy ra BC = $\sqrt{10}$.
   Vậy  $|2\overrightarrow{a}+2\overrightarrow{b}|=\left|2\overrightarrow{BC}\right|=2\left|\overrightarrow{BC}\right|=2BC=2\sqrt{10}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi MA→+MB→+MC→=3MG→.
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

   Trả lời:

   +) Giả sử tam giác ABC có trọng tâm G, ta cần chứng minh $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.
   Vì G là trọng tâm của tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.
   Với điểm M bất kì ta có: $\overrightarrow{MA}=\overrightarrow{MG}+\overrightarrow{GA}$, $\overrightarrow{MB}=\overrightarrow{MG}+\overrightarrow{GB}$, $\overrightarrow{MC}=\overrightarrow{MG}+\overrightarrow{GC}$.
   Khi đó: 
   $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=(\overrightarrow{MG}+\overrightarrow{GA})+(\overrightarrow{MG}+\overrightarrow{GB})+(\overrightarrow{MG}+\overrightarrow{GC})$
   $=3\overrightarrow{MG}+(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC})$ $=3\overrightarrow{MG}+\overrightarrow{0}=3\overrightarrow{MG}$.
   Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

   +) Giả sử tam giác ABC có 2 điểm M, G thỏa mãn $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$, ta cần chứng minh G là trọng tâm của tam giác ABC.
   Ta có: $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
   $\iff \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MG}=\overrightarrow{0}$
   $\iff (\overrightarrow{MA}-\overrightarrow{MG})+(\overrightarrow{MB}-\overrightarrow{MG})+(\overrightarrow{MC}-\overrightarrow{MG})=\overrightarrow{0}$
   $\iff \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
   Vậy G là trọng tâm của tam giác ABC.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
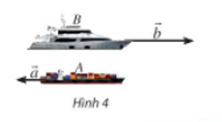
4. Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biểu diễn vectơ vận tốc b→ của tàu B theo vectơ vận tốc a→ của tàu A.
   
   

   Câu hỏi:
   

   Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biểu diễn vectơ vận tốc $\overrightarrow{b}$ của tàu B theo vectơ vận tốc $\overrightarrow{a}$ của tàu A.
   

   Trả lời:

   Tàu A đi theo hướng từ đông sau tây, tàu B đi theo hướng từ tây sang đông nên hai tàu đi ngược hướng nhau. Do đó vectơ vận tốc của tàu A là $\overrightarrow{a}$ và vectơ vận tốc của tàu B là $\overrightarrow{b}$ là hai vectơ ngược hướng.
   Ta có: $\left|\overrightarrow{a}\right|=20$ hải lí/giờ, $\left|\overrightarrow{b}\right|=50$ hải lí/giờ.
   Suy ra: $\frac{\left|\overrightarrow{b}\right|}{\left|\overrightarrow{a}\right|}=\frac{50}{20}=\frac{5}{2}\Rightarrow \left|\overrightarrow{b}\right|=\frac{5}{2}\left|\overrightarrow{a}\right|$.

   Vì hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ngược hướng và $\left|\overrightarrow{b}\right|=\frac{5}{2}\left|\overrightarrow{a}\right|$.
   Do vậy $\overrightarrow{b}=-\frac{5}{2}\overrightarrow{a}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hai vectơ a→ và b→ cùng phương, b→ khác 0→ và cho c→=|a→||b→|.b→. So sánh độ dài và hướng của hai vectơ a→ và c→
   
   

   Câu hỏi:
   

   Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương, $\overrightarrow{b}$ khác $\overrightarrow{0}$ và cho $\overrightarrow{c}=\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}.\overrightarrow{b}$. So sánh độ dài và hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{c}$

   Trả lời:

   Vì $\left|\overrightarrow{a}\right|\ge 0,\left|\overrightarrow{b}\right|>0$  (độ dài của vectơ và $\overrightarrow{b}$ khác $\overrightarrow{0}$).
   Nên $\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}\ge 0$.
   Mà $\overrightarrow{c}=\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}.\overrightarrow{b}$ nên vectơ $\overrightarrow{c}$ cùng hướng với vectơ $\overrightarrow{b}$.
   Do đó vectơ $\overrightarrow{c}$ cùng phương với $\overrightarrow{b}$, mà vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương và $\overrightarrow{b}$ khác $\overrightarrow{0}$.
   Nên hai vectơ $\overrightarrow{a}$ và $\overrightarrow{c}$ cùng phương.
   Ta lại có: $\left|\overrightarrow{c}\right|=|\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}.\overrightarrow{b}|=\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}.\left|\overrightarrow{b}\right|=\left|\overrightarrow{a}\right|$.
   Vậy hai vectơ $\overrightarrow{a}$ và $\overrightarrow{c}$ cùng độ dài và cùng phương.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====