Câu hỏi:
Cho hàm số y = \(\frac{{ – 2}}{x}\). Chứng tỏ hàm số đã cho đồng biến trên khoảng (–∞; 0) và (0; +∞).
Trả lời:
Lời giải
Đặt y = f(x) = \(\frac{{ – 2}}{x}\).
Tập xác định của hàm số D = ℝ \ {0}.
Lấy x1, x2 ∈ (–∞; 0) thỏa mãn x1 < x2 < 0
Vì x1 < x2 nên \(\frac{2}{{{x_1}}} > \frac{2}{{{x_2}}}\) ⇒ \(\frac{{ – 2}}{{{x_1}}} < \frac{{ – 2}}{{{x_2}}}\) hay f(x1) < f(x2).
Do đó hàm số đồng biến trên khoảng (–∞; 0).
Lấy x1, x2 ∈ (0; +∞) thỏa mãn 0 < x1 < x2
Vì x1 < x2 nên \(\frac{2}{{{x_1}}} > \frac{2}{{{x_2}}}\) ⇒ \(\frac{{ – 2}}{{{x_1}}} < \frac{{ – 2}}{{{x_2}}}\) hay f(x1) < f(x2).
Do đó hàm số đồng biến trên khoảng (0; +∞).
Vậy hàm số đồng biến trên khoảng (–∞; 0) và (0; +∞).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. x + 2y = 3.
B. y = \(\sqrt {{x^2} – 2x} \).
C. y = \(\frac{1}{x}\).
D. x2 + y2 = 4.
Câu hỏi:
Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. x + 2y = 3.
B. y = \(\sqrt {{x^2} – 2x} \).
C. y = \(\frac{1}{x}\).
D. x2 + y2 = 4.Trả lời:
Lời giải
Đáp án đúng là D
Xét công thức x + 2y = 3 ⇔ y = \( – \frac{1}{2}\)x + 3;
Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.
Xét công thức y = \(\sqrt {{x^2} – 2x} \)
Với mỗi giá trị của x ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.
Xét công thức y = \(\frac{1}{x}\)
Với mỗi giá trị x ≠ 0 ta xác định được duy nhất một giá trị của y nên công thức này y là hàm số của x.
Xét công thức: x2 + y2 = 4 ⇔ y2 = – x2 + 4 ⇔ y = \( \pm \sqrt { – {x^2} + 4} \).
Ta thấy ở công thức này, với mỗi giá trị của x thỏa mãn điều kiện – x2 + 4 ≥ 0 ta xác định được 2 giá trị của y. Do đó công thức này không biểu diễn y là hàm số của x.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đồ thị hàm số y = f(x) ở Hình 4. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 1.
C. Hàm số đồng biến trên khoảng (– 1; +∞), nghịch biến trên khoảng ( – ∞; – 1).
D. Hàm số đồng biến trên ℝ.
Câu hỏi:
Cho đồ thị hàm số y = f(x) ở Hình 4. Phát biểu nào sau đây là đúng?
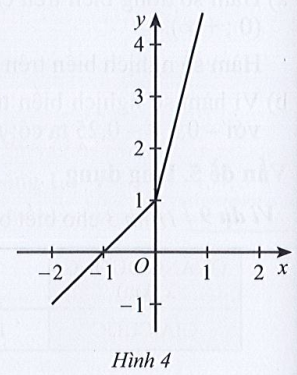
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 1.
C. Hàm số đồng biến trên khoảng (– 1; +∞), nghịch biến trên khoảng ( – ∞; – 1).
D. Hàm số đồng biến trên ℝ.Trả lời:
Lời giải
Đáp án đúng là D
Quan sát đồ thị ta thấy:
Hàm số xác định trên ℝ, và trên ℝ hàm số đi lên nên hàm đồng biến trên ℝ. Do đó C sai và D đúng.
Đồ thị hàm số cắt Ox tại điểm có hoành độ bằng – 1. Do đó A sai.
Đồ thị hàm số cắt Oy tại điểm có tung độ bằng 1. Do đó B sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm tập xác định của mỗi hàm số sau:
y = – x3 + 4x – 1;
Câu hỏi:
Tìm tập xác định của mỗi hàm số sau:
y = – x3 + 4x – 1;Trả lời:
Lời giải
Biểu thức – x3 + 4x – 1 xác định với mọi giá trị của x ∈ ℝ.
Do đó tập xác định của hàm số y = – x3 + 4x – 1 là D = ℝ.
Vậy D = ℝ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- y = \(\sqrt {5 – 6x} \);
Câu hỏi:
y = \(\sqrt {5 – 6x} \);
Trả lời:
Lời giải
Biểu thức \(\sqrt {5 – 6x} \) xác định khi 5 – 6x ≥ 0 ⇔ x ≤ \(\frac{5}{6}\).
Do đó tập xác định của hàm số y = \(\sqrt {5 – 6x} \) là D = \(\left( { – \infty ;\frac{5}{6}} \right]\).
Vậy D = \(\left( { – \infty ;\frac{5}{6}} \right]\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- y = \(\frac{4}{{3x + 1}}\);
Câu hỏi:
y = \(\frac{4}{{3x + 1}}\);
Trả lời:
Lời giải
Biểu thức \(\frac{4}{{3x + 1}}\) xác định khi 3x + 1 ≠ 0 ⇔ x ≠ \( – \frac{1}{3}\).
Do đó tập xác định của hàm số y = \(\frac{4}{{3x + 1}}\) là D = ℝ \ \(\left\{ { – \frac{1}{3}} \right\}\).
Vậy D = ℝ \ \(\left\{ { – \frac{1}{3}} \right\}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====